原码、反码、补码、移码的公式推导

一点废话

关于这几个码早在n年前看过的了，后来也只记得补码，正好今天看到了这几个码的公式，就顺便记录下并尝试推导下。

很多同学可能觉得直接把公式记住就行了，但我还是觉得复习不能光图快，在理解的基础上去记会更好，或者压根儿就不用记。

原码

规则 ：0表示正号，1表示负号，其余n-1位表示数值的绝对值。
按照这个定义，我们很容易写出(n = 4)：

（十进制）5 = （二进制）0101
（十进制）-5 = （二进制）1101

本来觉得原码挺简单，但是看了这么个公式，不免心中一居灵。

其实静心想想也不难。

我们先看下整数。

1. 取值范围

因为n位中首位表示符号，所以只有后n-1位表示数值，所能表示的最大位为后n-1全是1的情形，其十进制值为：

2⁰ + 2¹ + … + 2^n-2 = 2^n-1 - 1(等比数列求和公式)

比如上面n=4时，所能表示最大的正数为7，就是0111。
同理我们可以推出下限为-(2^n-1 - 1)。

细心的同学应该发现整数的两个定义域中都有0，这是由原码的定义决定的:
十进制0在原码中有两种表示：
+0 = 0 00…0
-0 = 1 00…0

2. 表达式

当X$\in$[0, 2^n-1 - 1]时，X为其本身很好理解，那么X$\in$[2^n-1 - 1,0]，为什么是2^n-1 - 1 + |X|呢？

因为负数就是在正数的基础上把最高位由0改成了1，对应的十进制为增加了2^n-1。

再来看看小数。

在看小数之前，我们先学习下定点小数的表示，n位
(a₀ a₁ … a_n-1）表示的十进制小数为：
a₀ * 2⁰ + a₁ * 2^-1 + … + a_n-1 * 2^-1(n-1) 。
如0101 = 0 + 1/2 + 0 + 1/8 = 5/8 = 0.125
所以在最高位将0换成1，实际上是加了2⁰ = 1。

反码

规则：0变成1，1变成0。

下面我们推导为什么负数是2ⁿ - 1 - X。

当X > 0时，其二进制n位表示为：
(0 a₁ … a_n-1），其中a_i = 0或1，i$\in$(0,n)。

即X = 0 * 2^n-1 + a₁ * 2^n-2 + … + a_n-1 * 2⁰

当X < 0时，则根据反码规则，其二进制X的n位表示为：
(1 1-a₁ … 1-a_n-1），其中a_i = 0或1，i$\in$(0,n)。

即X = 1 * 2^n-1 + (1-a₁) * 2^n-2 + (1-a_n-1) * 2⁰ = 2^n-1 + 2^n-2 + 2⁰ - |X| = 2ⁿ - 1 + X

关于小数场景，我们可以同样推导出：
X < 0时，X = 1 * 2⁰ + (1-a₁) * 2^-1 + … + (1-a_n-1) * 2^-(n-1) = 2 - 2^-(n-1) + X

补码

规则：负数为正数的反码加1。

1. 取值范围
相比原码和反码，补码的取值范围多了一个-2^n-1，这是因为0只有一种表达。
2. 表达式
因为补码的变换是在反码的基础上+1，即在十进制上加了2⁰ = 1，所以负数的表达式中同样+1，结果为2ⁿ + X。

而在小数中，反码二进制+1其实是在其十进制上加了2^-(n-1)。

故结果为2 + X。

移码

规则：X上增加偏移量2^n-1。

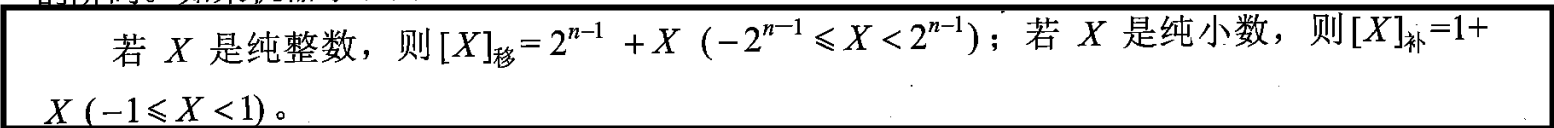
整数表达式由定义就可以得出。

小数为什么是1 + X呢？因为2^n-1个偏移量相当于在最高位加1，

所以是在X的基础上加了2⁰=1，故为1+X。
因为X$\in$[-1,1)，则只有x = -1时有溢出，此时溢出后结果为0₁₀，根据公式X[_补] = 1 + X也为0。

最后，我们再证明下：

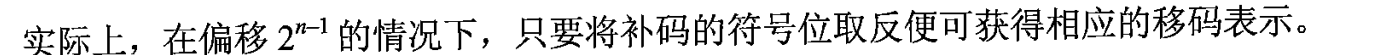
正数（无论是整数还是小数）没什么好说的，补码表示时最高位是0，偏移2^n-1就是把最高位改成1。

负数时，补码是取反加1，移码是加2^n-1，为什么两者转换后的结果只是最高位不一样呢？

从表达式看，负数补码为：2ⁿ + X, 移码为 2^n-1 + X，而2ⁿ + X = 2^n-1 + X + 2^n-1，也就是说把移码再偏移2^n-1就会变成补码，即取反最高位（考虑溢出）。

结后语

在复习过程中，我们不能为了考试而考试，更应该注重学习方法的培养，做到知其所以然。