北大软微校企合作课程作业

本文主要是介绍北大软微校企合作课程作业，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

作业一：使用intel oneAPI实现并行矩阵乘法

问题描述

编写⼀个基于oneAPI的C++/SYCL程序来执行矩阵乘法操作。需要考虑大尺寸矩阵的乘法操作以及不同线程之间的数据依赖关系。通常在实现矩阵乘法时，可以使用块矩阵乘法以及共享内存来提高计算效率。

实验过程

众所周知，朴素的矩阵乘法运算的时间复杂度是O(n3)O(n^3)O(n3)，当然矩阵乘法有一些别的优化方式，例如Strassen矩阵乘法，基于分治进行了十次小矩阵加法和七次小矩阵乘法，时间复杂度优于O(n3)O(n^3)O(n3)。

但是采用递归算法实现的矩阵乘法往往有依赖关系，子问题数量也呈指数级增加，而我们的机器的线程数（或者说核数）是有限的，所以不能无限制的增加，将子问题派发给不同线程。

因此，在解决这个问题过程中，依然采用了O(n3)O(n^3)O(n3)复杂度的GEMM矩阵乘法算法，但是利用并行计算，我们可以缩短计算的时间，也就是达成一个加速比。

对矩阵进行分块计算，在这里只考虑了矩阵维度能对齐的情况，如果不能对齐tile（例如大小不是512，而是511，513，那么需要进行zero-padding）。实际上的分块（tile）大小和机器的缓存大小有关，因为需要考虑矩阵乘法的访问序列是一行与一列共同访问的，所以一旦tile太大，访问一列时就会频繁发生cache miss，访问A矩阵和B矩阵的行和列时也会频繁触发switch，影响性能。

代码

24行开始定义并行任务队列q，采用nd-parallel思想，nd_item的维数是2。 31~33行使用的是定义的局部内存，防止每一次计算的临时结果都被写入原来的矩阵C中，而是将结果都在共享内存中写好了之后才写入结果矩阵。

然后使用朴素矩阵乘法实现了normal的矩阵计算，用于验算以及测试并行加速比。

#include <chrono>
#include <iostream>
#include <sycl/sycl.hpp>#define random_float() (rand() / double(RAND_MAX))using namespace sycl;const int tileX = 8;
const int tileY = 8;double matrix_multiply_parallel(float *A, float *B, float *C, int M, int N, int K, int BLOCK, sycl::queue &q) {auto grid_rows = M / tileY;auto grid_cols = N / tileX;auto local_ndrange  = range<2>(BLOCK, BLOCK);auto global_ndrange = range<2>(grid_rows, grid_cols);double duration = 0.0f;auto e = q.submit([&](sycl::handler &h) {h.parallel_for(sycl::nd_range<2>(global_ndrange, local_ndrange), [=](sycl::nd_item<2> index) {int row = tileY * index.get_global_id(0);int col = tileX * index.get_global_id(1);float sum[tileY][tileX] = {0.0f};float subA[tileY] = {0.0f};float subB[tileX] = {0.0f};for (int k = 0; k < N; k++) {for(int m = 0; m < tileY; m++) {subA[m] = A[(row + m) * N + k];} for(int p = 0; p < tileX; p++) {subB[p] = B[k * N + p + col];} for (int m = 0; m < tileY; m++) {for (int p = 0; p < tileX; p++) {sum[m][p] += subA[m] * subB[p];}}}for (int m = 0; m < tileY; m++) {for (int p = 0; p < tileX; p++) {C[(row + m) * N + col + p] = sum[m][p];}}});});e.wait();duration += (e.get_profiling_info<info::event_profiling::command_end>() -e.get_profiling_info<info::event_profiling::command_start>()) /1000.0f/1000.0f;return(duration);
}double matrix_multiply_normal(float *cA, float *cB, float *cC, int M, int N, int K) {double duration = 0.0;std::chrono::high_resolution_clock::time_point s, e;s = std::chrono::high_resolution_clock::now();for(int i = 0; i < M; i++) {for(int j = 0; j < N; j++) {float sum = 0.0f;for(int k = 0; k < K; k++) {sum +=  cA[i * K + k] * cB[k * N  + j];}cC[i * N + j] = sum;}}e = std::chrono::high_resolution_clock::now();duration = std::chrono::duration<float, std::milli>(e - s).count();return(duration);
}int verify(float *normal_res, float *parallel_res, int length){int err = 0;for(int i = 0; i < length; i++) {if( fabs(normal_res[i] - parallel_res[i]) > 1e-3) {err++;printf("\n%lf, %lf, %d %lf", normal_res[i], parallel_res[i], i, fabs(normal_res[i]-parallel_res[i]));} }return(err);
}int gemm(const int M, const int N, const int K, const int block_size,const int iterations, sycl::queue &q) {std::cout << "Problem size: c(" << M << "," <<  N << ") ="<< " a(" << M << "," << K << ") *" << " b(" << K << "," << N << ")\n";auto A = malloc_shared<float>(M * K, q);auto B = malloc_shared<float>(K * N, q);auto C = malloc_shared<float>(M * N, q);auto C_host = malloc_host<float>(M * N, q);for(int i=0; i < M * K; i++) {A[i] = random_float();}for(int i=0; i < K * N; i++) {B[i] = random_float();}for(int i=0; i < M * N; i++) {C[i] = 0.0f;C_host[i] = 0.0f;}double flopsPerMatrixMul= 2.0 * static_cast<double>(M) * static_cast<double>(N) * static_cast<double>(K);double duration_parallel = 0.0f;double duration_normal = 0.0f;int warmup = 10;for (int run = 0; run < iterations + warmup; run++) {float duration = matrix_multiply_parallel(A, B, C, M, N, K, block_size, q);if(run >= warmup) duration_parallel += duration;}duration_parallel = duration_parallel / iterations;warmup = 2;for(int run = 0; run < iterations/2 + warmup; run++) {float duration = matrix_multiply_normal(A, B, C_host, M, N, K);if(run >= warmup) duration_normal += duration;}duration_normal = duration_normal / iterations/2;int errCode = 0;if(errCode > 0) printf("\nThere are %d errors\n", errCode);printf("\nGEMM size M = %d, N = %d, K = %d", M, N, K);printf("\nWork-Group size = %d * %d, tile_X = %d, tile_Y = %d", block_size, block_size, tileX, tileY);printf("\nPerformance Flops = %lf, \n" "Parallel Computation Time = %lf (ms); \n""Normal Computaiton Time = %lf (ms); \n""Speedup = %lf\n", flopsPerMatrixMul, duration_parallel, duration_normal, duration_normal/duration_parallel);free(A, q);free(B, q);free(C, q);free(C_host, q);return(errCode);
}int main() {auto propList = sycl::property_list {sycl::property::queue::enable_profiling()};queue my_queue(default_selector_v , propList);int errCode = gemm(512, 512, 512, 4,             10,               my_queue);return(errCode);
}

运行结果

运行结果如图。在使用Sycl dpc++编译以后，shell里直接运行，使用的DevCloud没有GPU core，所以并行计算版本和普通版本都是CPU core的计算速度。

总结

这次实验我进行了矩阵乘法的实验，了解到了除了降低算法复杂度以外，使用并行分块的方式降低计算时间的方式，也体验了Intel OneAPI的使用全流程，在DevCloud上把程序写出来并运行起来，获得了预期的结果。这次实验拓宽了我对并行计算的认识，也让我有机会接触到Intel OneAPI这一套全新的工具包和并行编程框架。

作业二：使用intel oneAPI实现并行归并排序

问题描述

使用基于oneAPI的C++/SYCL实现⼀个高效的并行归并排序。需要考虑数据的分割和合并以及线程之间的协作。

思路

以下代码是一个并行归并排序算法的实现，使用了SYCL库，这是一个能够实现异构计算的C++标准库。代码包括了串行和并行排序的过程，并能在主机和GPU上运行。

mergeSequences函数：该函数用于合并两个已排序的子序列。它首先创建一个临时的SYCL缓冲区（tempBuf），用于存储合并的结果。然后，它将序列合并的工作提交给SYCL队列（deviceQueue），该队列负责在设备上异步执行合并操作。最后，它将合并后的数据复制回原始数据缓冲区。

parallelMergeSort函数：这是主要的排序函数，它使用分而治之的方法将数组分成更小的部分进行排序。首先检查是否到达递归的基础条件（start < end）。当递归深度maxDepth降到0以下时，使用串行排序；否则，继续递归划分数组，并在每个部分上调用自己，最后合并这些已排序的部分。

main函数：这是程序的入口点。它首先创建了一个大小为2的20次幂的数组，并用随机数填充。然后，它创建了一个SYCL队列和一个数据缓冲区，用于在设备上运行排序算法。调用parallelMergeSort函数进行排序，并验证排序是否正确。

代码

 %%writefile src/parallelsort.cpp#include <CL/sycl.hpp>#include <vector>#include <iostream>#include <algorithm>// 不再使用整个命名空间using namespace sycl;// 串行归并排序，使用标准库中的排序算法void serialMergeSort(std::vector<int>& data) {std::sort(data.begin(), data.end());}// 合并两个有序子序列void mergeSequences(queue &deviceQueue, buffer<int, 1> &bufferData, int start, int middle, int end) {std::vector<int> tempBuffer(end - start + 1);buffer<int, 1> tempBuf(tempBuffer.data(), tempBuffer.size());deviceQueue.submit([&](handler &cgh) {auto dataAcc = bufferData.get_access<access::mode::read_write>(cgh);auto tempAcc = tempBuf.get_access<access::mode::write>(cgh);cgh.parallel_for(range<1>(end - start + 1), [=](id<1> idx) {int leftIndex = start;int rightIndex = middle + 1;int tempIndex = idx[0];if (leftIndex <= middle && (rightIndex > end || dataAcc[leftIndex] < dataAcc[rightIndex])) {tempAcc[tempIndex] = dataAcc[leftIndex++];} else {tempAcc[tempIndex] = dataAcc[rightIndex++];}});});deviceQueue.wait();deviceQueue.submit([&](handler &cgh) {auto dataAcc = bufferData.get_access<access::mode::write>(cgh);auto tempAcc = tempBuf.get_access<access::mode::read>(cgh);cgh.parallel_for(range<1>(end - start + 1), [=](id<1> idx) {dataAcc[start + idx[0]] = tempAcc[idx[0]];});});deviceQueue.wait();}// 并行归并排序void parallelMergeSort(queue &deviceQueue, buffer<int, 1> &bufferData, int start, int end, int maxDepth) {if (start < end) {if (maxDepth <= 0) {auto hostData = bufferData.get_access<access::mode::read_write>();std::vector<int> localData(hostData.get_pointer() + start, hostData.get_pointer() + end + 1);serialMergeSort(localData);for (int i = start; i <= end; ++i) {hostData[i] = localData[i - start];}} else {int middle = (start + end) / 2;parallelMergeSort(deviceQueue, bufferData, start, middle, maxDepth - 1);parallelMergeSort(deviceQueue, bufferData, middle + 1, end, maxDepth - 1);mergeSequences(deviceQueue, bufferData, start, middle, end);}}}int main() {// 设置数组的大小const int numElements = 1 << 20;std::vector<int> inputData(numElements);// 生成随机数据std::generate(inputData.begin(), inputData.end(), [] { return std::rand() % 100; });queue deviceQueue;buffer<int, 1> dataBuf(inputData.data(), range<1>(numElements));parallelMergeSort(deviceQueue, dataBuf, 0, numElements - 1, 4);// 获取并输出排序后的数据auto sortedBuffer = dataBuf.get_access<access::mode::read>();for (int i = 0; i < numElements; ++i) {if(i > 5000 && i < 5100) {std::cout << sortedBuffer[i] << " ";}}std::cout << "\n";// 验证数组是否已正确排序bool isSorted = std::is_sorted(sortedBuffer.get_pointer(), sortedBuffer.get_pointer() + numElements);std::cout << "Array is sorted: " << (isSorted ? "Yes" : "No") << std::endl;return 0;}

运行结果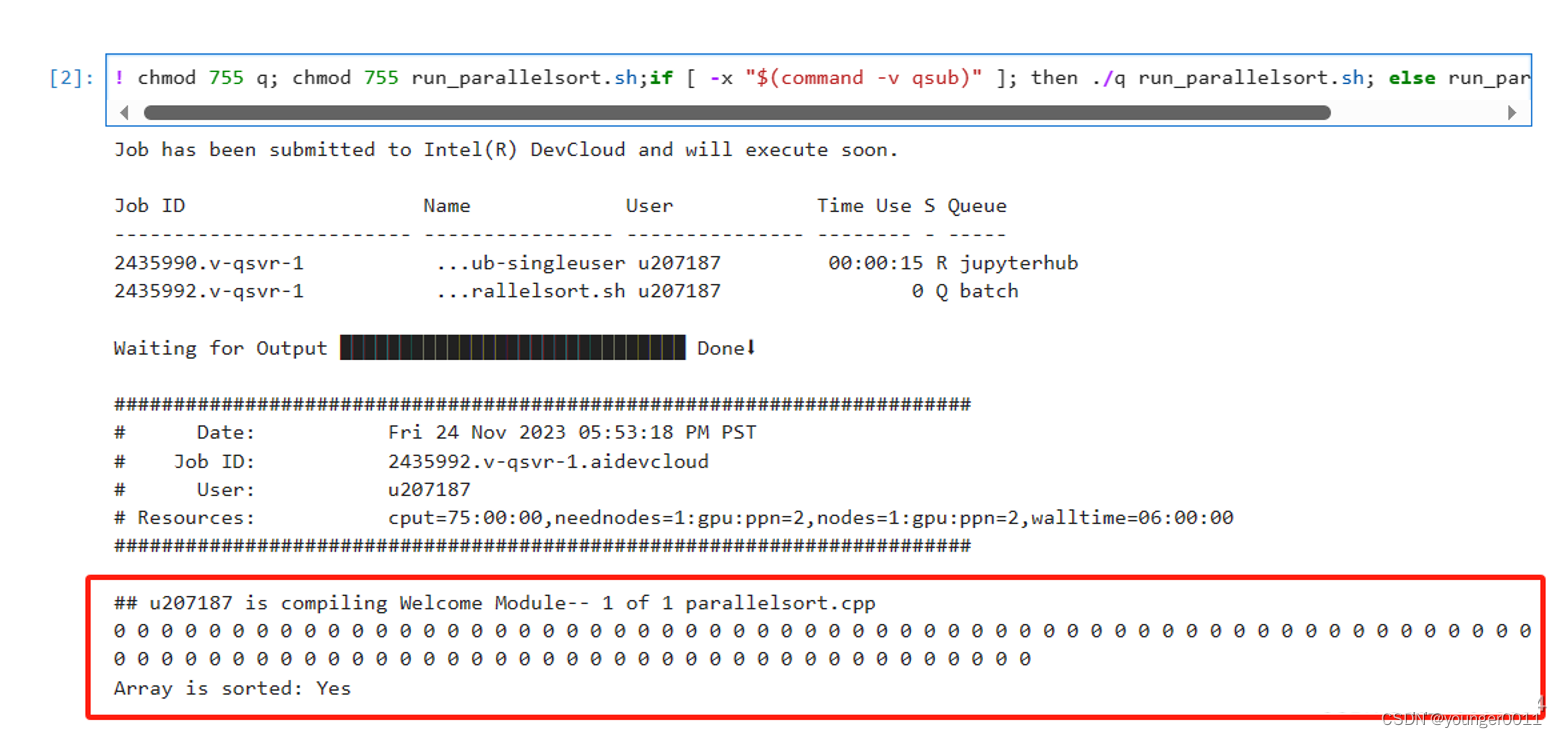

作业三：使用intel oneAPI实现图像卷积并行加速

问题描述

使用基于oneAPI的C++/SYCL实现一个用于计算图像的卷积操作。输⼊为一个图像矩阵和一个卷积核矩阵，输出为卷积后的图像。

思路

为了简洁，假设图像和卷积核是正方形的，并且卷积核的尺寸较小。定义一个convolve2D函数，该函数接受输入图像、卷积核、输出图像的向量，以及图像和卷积核的尺寸。

通过定义缓冲区将输入图像、卷积核和输出图像传递给设备。

使用q.submit将任务提交到SYCL队列。定义一个parallel_for内核，其范围为输出图像的尺寸，减去卷积核的大小加

代码

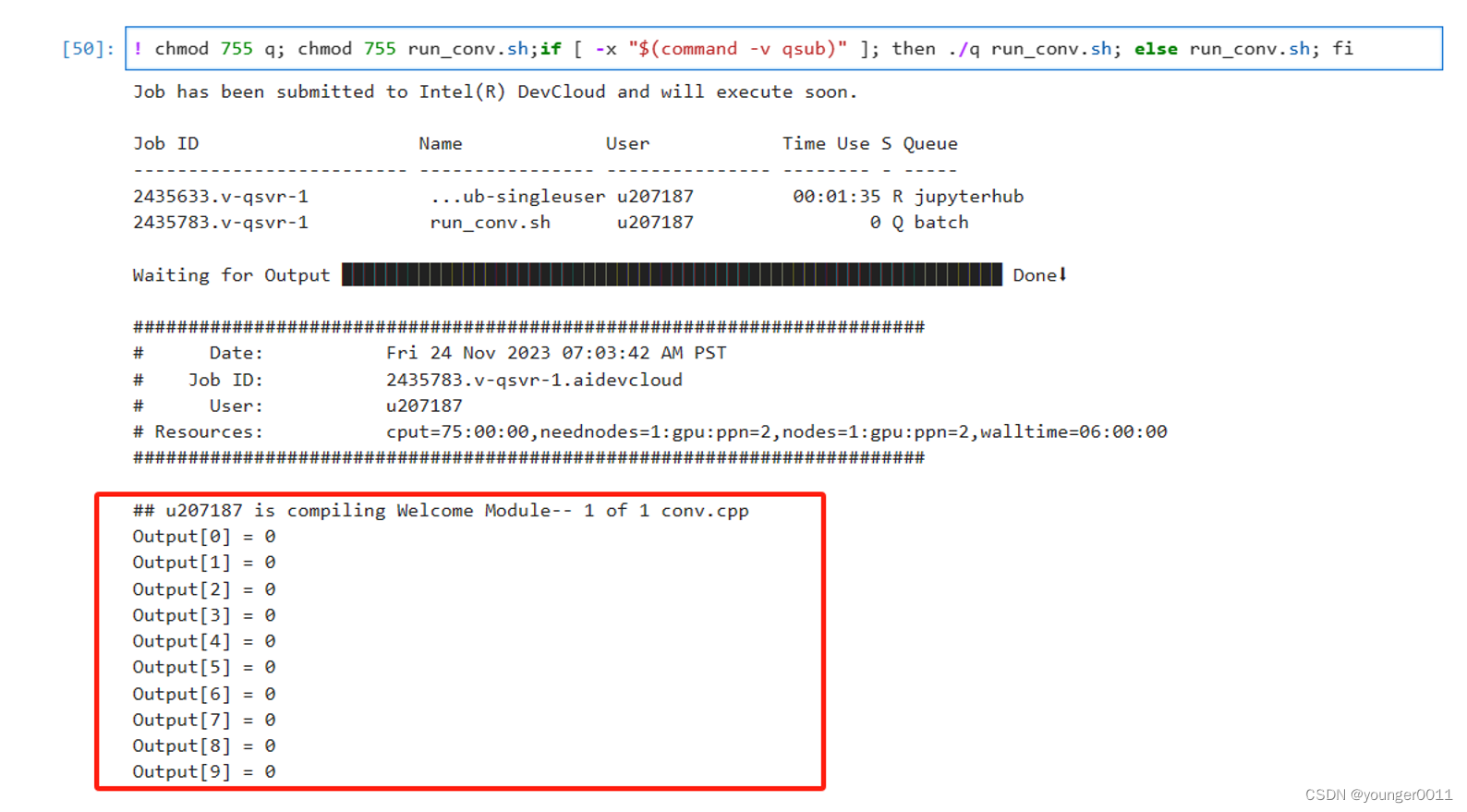
 %%writefile src/conv.cpp#include <CL/sycl.hpp>#include <vector>#include <iostream>using namespace sycl;// 函数：执行卷积操作void convolve2D(const std::vector<float>& inputImage, const std::vector<float>& kernel,std::vector<float>& outputImage, int imageSize, int kernelSize, queue& q) {// 创建SYCL缓冲区buffer<float, 2> bufferInput(inputImage.data(), range<2>(imageSize, imageSize));buffer<float, 2> bufferKernel(kernel.data(), range<2>(kernelSize, kernelSize));buffer<float, 2> bufferOutput(outputImage.data(), range<2>(imageSize, imageSize));// 提交任务到队列q.submit([&](handler& cgh) {// 获取访问器auto accInput = bufferInput.get_access<access::mode::read>(cgh);auto accKernel = bufferKernel.get_access<access::mode::read>(cgh);auto accOutput = bufferOutput.get_access<access::mode::write>(cgh);// 定义卷积操作cgh.parallel_for(range<2>(imageSize - kernelSize + 1, imageSize - kernelSize + 1), [=](id<2> idx) {int x = idx[0];int y = idx[1];float sum = 0.0f;// 遍历卷积核for (int i = 0; i < kernelSize; ++i) {for (int j = 0; j < kernelSize; ++j) {sum += accInput[x + i][y + j] * accKernel[i][j]; // 应用卷积核}}accOutput[x + kernelSize/2][y + kernelSize/2] = sum; // 存储卷积结果});}).wait(); // 等待队列中的任务完成}int main() {// 图像和卷积核的大小const int imageSize = 1024; // 假设为1024x1024const int kernelSize = 3;   // 假设为3x3// 初始化输入图像、卷积核和输出图像std::vector<float> inputImage(imageSize * imageSize, 1.0f); // 示例：所有值初始化为1std::vector<float> kernel = {0.0625f, 0.125f, 0.0625f,0.125f, 0.25f, 0.125f,0.0625f, 0.125f, 0.0625f}; // 示例：高斯模糊核std::vector<float> outputImage(imageSize * imageSize, 0.0f);// 创建SYCL队列queue q;// 执行卷积操作convolve2D(inputImage, kernel, outputImage, imageSize, kernelSize, q);// 输出结果（这里只输出前10个元素进行验证）for (int i = 0; i < 10; ++i) {std::cout << "Output[" << i << "] = " << outputImage[i] << std::endl;}return 0;}