本文主要是介绍【数据结构取经之路】栈，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
引言
栈的性质
顺序栈
栈的基本操作
初始化
销毁
插入
删除
判空
取栈顶元素
栈的大小
完整代码：
引言
栈(stack)，可以用数组实现，也可以用链表实现。用数组实现的栈叫顺序栈，用链表实现的栈叫链式栈，本文讲解的是顺序栈。栈，作为一种特殊的数据结构，在一些方面有着重要用途，例如，快速排序的非递归实现就需要借助栈来完成。
栈的性质
栈是限定仅在栈顶进行插入或删除操作的线性表。它是遵循“后进先出”的原则的，队列正好与之相反。
顺序栈
底层用数组实现，当数组空间不够用时就扩容。这些操作和用数组来实现通讯录如出一辙，想必大家已轻车熟路，这里就点到为止了。
栈的基本操作
因为顺序栈的底层是用数组实现，所以本质上还是在操作数组。
初始化
初始化操作一般有两种，第一种，在初始化时就给数组分配一定的空间，第二种，初始化时不给分配空间，第一次插入数据时才个数组分配空间。这两种方法用哪一种都无可厚非，按自己喜好来就好，这里呢我就偏爱第二种方法。
代码：
typedef int StackDataType;typedef struct Stack
{StackDataType* a;int capacity;//容量int top;
}Stack;void StackInit(Stack* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;//容量pst->top = 0;
}
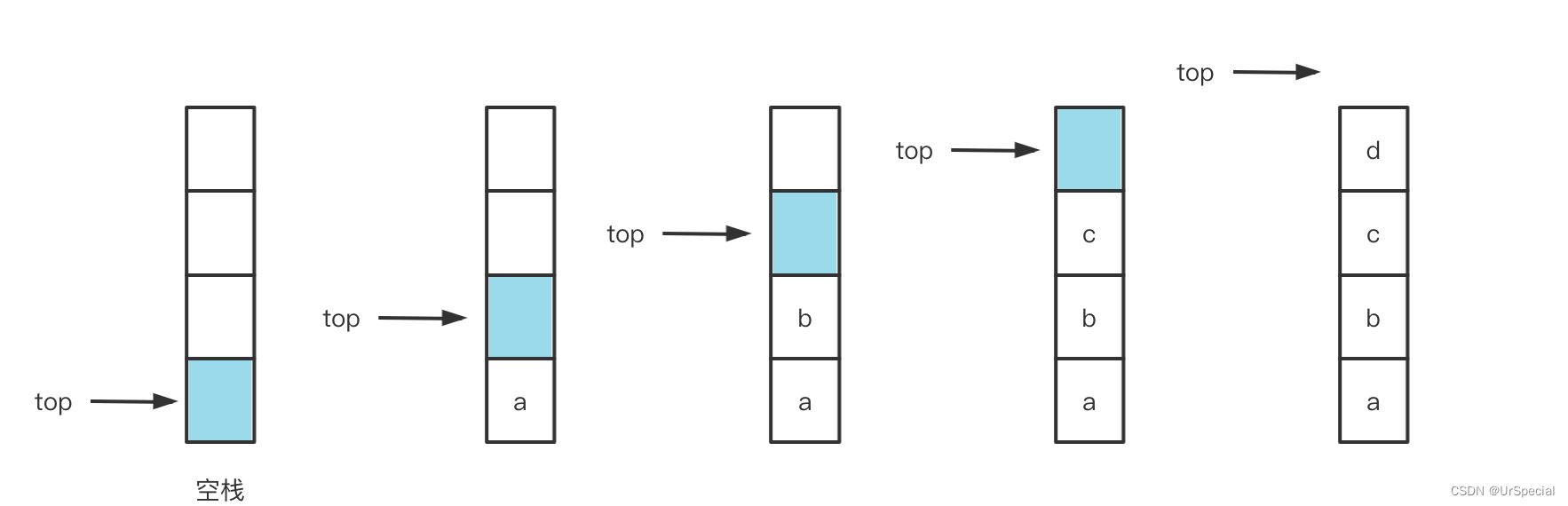需要注意的一个细节是，top指向的是栈顶元素的下一个，以防返回栈顶元素时出现错误。细心观察也会发现，top的值就是栈中的元素个数，这样，返回栈的大小就简单了。
销毁
因为底层使用数组实现，所以要释放数组空间只需要free一把就行了。
void StackDestroy(Stack* pst)
{assert(pst);pst->capacity = 0;pst->top = 0;free(pst->a);
}插入
底层用数组实现，那么在插入时就有可能面临着空间不够的问题，所以在插入之前，需要判断数组是否已满。
代码：
void StackPush(Stack* pst, StackDataType x)
{assert(pst);if (pst->capacity == pst->top){int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;StackDataType* tmp = (StackDataType*)realloc(pst->a, sizeof(StackDataType) * newCapacity);if (tmp == NULL){perror("malloc fail");return;}pst->a = tmp;}pst->a[pst->top] = x;pst->top++;
}
删除
顺序栈的删除实际上就是数组最后一个元素的删除，不需要挪动数据，top--即可，这样即使数组中还存在该元素，但是已经访问不到了。
代码：
void StackPop(Stack* pst)
{assert(pst);pst->top--;
}判空
空的特征是：top为0，所以只需要判断top是否为0即可。
代码：
bool StackEmtpy(Stack* pst)
{assert(pst);return pst->top == 0;
}取栈顶元素
栈顶元素的下标为top-1，返回该下标对应的值即可。
代码：
StackDataType StackTop(Stack* pst)
{assert(pst);return pst->a[pst->top - 1];
}虽然简单，但请不要写成pst->a[pst->top--]. 后置--是有副作用的，也就是说会改变top的值，但这里不需要改变top的值。当然，这种错误是极小概率事件，只是顺便提一提。
栈的大小
top的值就是栈的大小，所以返回top即可。
代码：
int StackSize(Stack* pst)
{assert(pst);return pst->top;
}完整代码：
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int StackDataType;typedef struct Stack
{StackDataType* a;int capacity;//容量int top;
}Stack;void StackInit(Stack* pst);void StackDestroy(Stack* pst);void StackPush(Stack* pst, StackDataType x);void StackPop(Stack* pst);bool StackEmtpy(Stack* pst);StackDataType StackTop(Stack* pst);int StackSize(Stack* pst);void StackInit(Stack* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;pst->top = 0;
}void StackDestroy(Stack* pst)
{assert(pst);pst->capacity = 0;pst->top = 0;free(pst->a);
}void StackPush(Stack* pst, StackDataType x)
{assert(pst);if (pst->capacity == pst->top){int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;StackDataType* tmp = (StackDataType*)realloc(pst->a, sizeof(StackDataType) * newCapacity);if (tmp == NULL){perror("malloc fail");return;}pst->a = tmp;}pst->a[pst->top] = x;pst->top++;
}void StackPop(Stack* pst)
{assert(pst);pst->top--;
}bool StackEmtpy(Stack* pst)
{assert(pst);return pst->top == 0;
}StackDataType StackTop(Stack* pst)
{assert(pst);return pst->a[pst->top - 1];
}int StackSize(Stack* pst)
{assert(pst);return pst->top;
}
这篇关于【数据结构取经之路】栈的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
