算法之 数组两端取数游戏

题目

  同学A与B玩取数游戏。即有一个2n项的数组，其中每个都是整数且对两位同学都是可见的，两位同学轮流从 两端 取走数字（假设A同学先取）。
  胜负评判：所取数之和较大者获胜（可能存在平局）。

分析

1. 如果题目问A同学的胜负情况，那可以直接回答胜或者平局，因为数组对两位同学都是可见的，都做出最佳决策的情况下肯定是先取者获胜，或者平局。
2. 如果题目问A同学最后会比B同学多多少分。那么可以用递归求解，我们拿一个具体的例子，{1,3,30,4}  很显然不能用贪心策略，让A同学直接取当前两端的较大值，因为那样的话，很大的30会被B取走，所以可以看出来两次取数之间有关联。我们可以看出来A同学应该取1，然后B同学取4，然后A取30，B取3，最终A同学得分为31，B为7。
   
   设 sum( i , j ) 为A同学从数组 a 下标的 i 处到 j 处这个范围下采取最佳决策后的得分与B同学的差值，所以我们最后要求的是sum( 0 , 3 )，表示A同学的最大得分
   那么思考每一步，是取左边的数还是右边的数呢？这取决于 a[左] - sum( 左+1，右)
   和 a[右] - sum( 左， 右-1 ) 哪个大。这里要注意不是 + 号 而是 - 号，因为A同学取完之后是B同学取。还要注意递归的终止条件。

 public static int fun(int[] a, int i, int j) {if(i +1 == j) return Math.abs(a[i]-a[j]);int temp1 = a[i] - fun(a, i+1, j);int temp2 = a[j] - fun(a, i, j-1);return Math.max(temp1,temp2);}

  鉴于以上递归过程中会大量重复计算值，可能会使递归栈的深度过大导致栈溢出，而且降低了性能，于是考虑使用Dynamic Programming动态规划来解决。
  和一般DP问题一样，有个二维数组来保存记录，DP[n][n] 和以上sum( i , j )的意义一样，n是原数组 a 的大小。
递归表达式：

DP[i][i] =a[i]
DP[i][j] = max(a[i]-DP[i+1][j], a[j]-DP[i][j-1])

写成代码的话就是：

public static int fun2(int[] nums) {int n = nums.length;int[][] dp = new int[n][n];for(int i = 0; i < n; i++)dp[i][i] = nums[i];for(int i = 0; i < n-1; i++)for(int j = i+1; j < n; j++)dp[j-i-1][j] = Math.max(nums[j-i-1] - dp[j-i][j], nums[j] - dp[j-i-1][j-1]);return dp[0][n-1];}

这里要注意的是这个矩阵的填写方向，for循环还有点难写。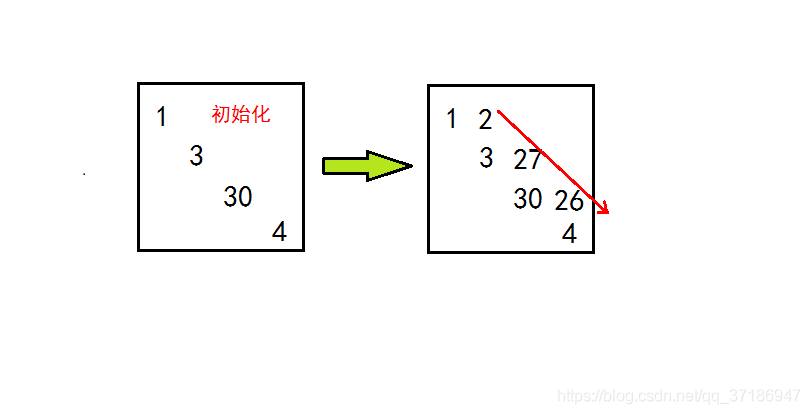

彩蛋

 以上方法在很久之前都见过，也没什么新意。稍加改动就可以求出A，B同学具体取的数字，但是在最近看一本《常用算法与程序设计》的时候，发现了这个题还有更简单粗暴的方式，复杂度是O(n)
 先求出序列中奇数号整数之和S1,再求出偶数号整数之和S2.
那么 | S1 - S2 | 就是A,B同学最终得分的差值了。而且，A同学不是取全体奇数号项，就是取全体偶数项，这个值得动脑筋想想。
还是例子 {1,3,30,4}，那么 S1 = 1+30 = 31， S2 = 2+4 = 6
那么要胜的A同学，先取奇数项，即1，然后剩下的能取的3和4都是偶数项，B会取较大的4，然后A继续取数，那么能取的一定是奇数项了。所以证明了取的数是全体奇数项。
由此可见，什么递归，动归，还是逻辑分析动脑筋最重要啊！