本文主要是介绍光度立体法的简化求解(已知特殊光源方向),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原理这个博主写的很好
如何获取物体表面的法向量?好好谈谈光度立体法-CSDN博客
Photometric Stereo 光度立体三维重建(一)——介绍-CSDN博客
不过当图片较大的时候,比如4048*4000这种量级的,矩阵很大,速度要10秒,加了openmp也需要2s;
如果我们知道一些先验知识,在特定的slant和titls角度,可以简化过程,提升速度(结果在最后)
四个光源在等高且titls分别为0,90,180,270;偏角均为slant = θ
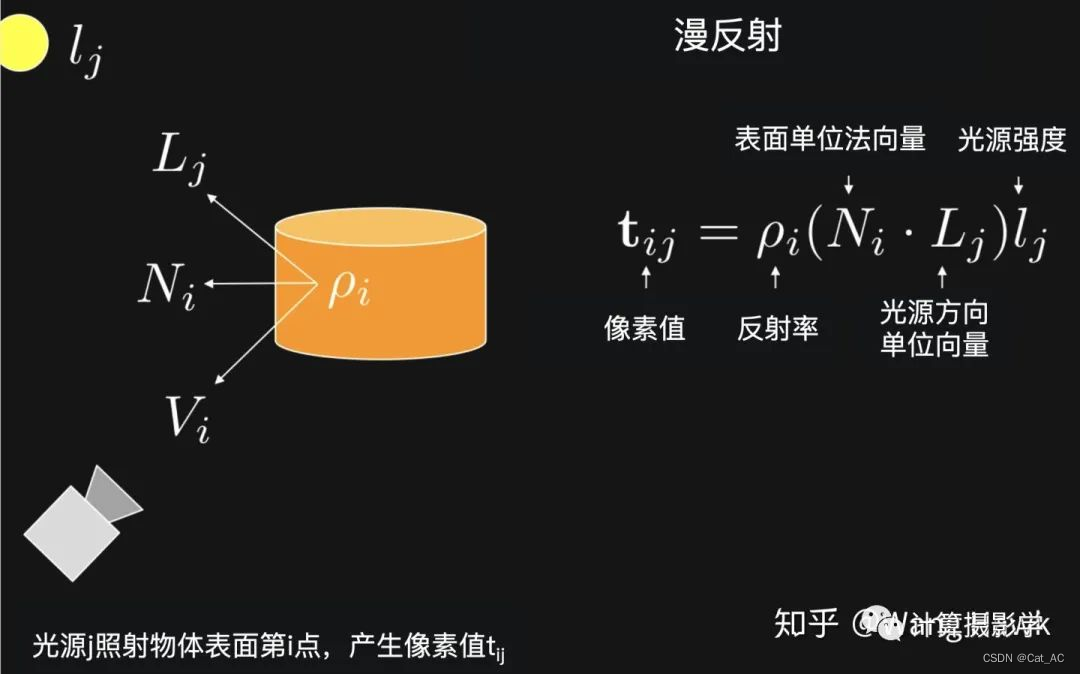
那么每个位置(x,y)在四个特殊的角度下,代入朗博公式有
其中,ρ反射率,l是光强
一式加三式,二式加四式有
那么有
一式减三式,二式减四式有
将
代入上面两个式子中
得到:
处理一下,得到:
上面两式子就是求出的法向量x分量,y分量.这样可以跳过大矩阵求逆相乘的溢出,减少耗时,速度提升很多.
下面是处理4048*4000图片的速度(均加了openmp)
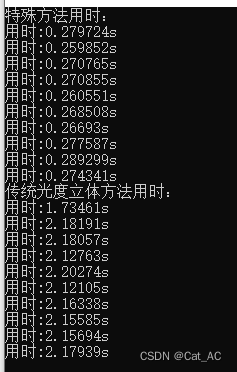
| 不加omp | 加omp | |
| 传统方法 | 10s | 2s |
| 特殊方法 | 0.7s | 0.2s |
这篇关于光度立体法的简化求解(已知特殊光源方向)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






