一维前缀和一维差分（下篇讲解二维前缀和二维差分）（超详细，python版，其他语言也很轻松能看懂）

本文主要是介绍一维前缀和一维差分（下篇讲解二维前缀和二维差分）（超详细，python版，其他语言也很轻松能看懂），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本篇博客讲解一维前缀和，一维差分，还会给出一维差分的模板题，下篇博客讲解 二维前缀和&二维差分。

一维前缀和：

接触过算法的小伙伴应该都了解前缀和，前缀和在算法中应用很广，不了解也没有关系，这里简单介绍一下什么是前缀和。

如数组a[0,1,2,3,4]，则数组a的前缀和为b[0,1,3,6,10]，也就是b[i] = a[i] + b[i - 1]，利用前缀和我们可以快速求出在数组a在区间[l,r]中的和为多少，如在[2，3]区间内数组a的和为b[3]-b[1] = 5。一维前缀和的递推公式为：b[i] = a[i] + b[i - 1]

一维差分：

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

什么意思？简单来说，如果存在一个数组a，数组a的前缀和数组为b，则数组a就是数组b的差分数组！b是a的前缀和数组！

简单说一种情况，有一个数组，现在需要对数组进行多次操作，每次操作都是在区间[l,r]上加上一个相同的数或者减掉一个相同的数，所有操作完成后，数组为多少？

如果暴力法的话，每次操作的时间复杂度都为O(n)，如果操作次数一多，算法可能就会超时，这是就需要用差分来处理这类问题，差分会将每次操作的时间复杂度都降为O(1)。

差分数组：

首先给定一个原数组a：a[1], a[2], a[3] , , , , a[n];

然后我们构造一个数组b ： b[1] ,b[2] , b[3] , , , b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +, , , , + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

考虑如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] =a [3] - a[2];

…

b[n] = a[n] - a[n-1];

差分时始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。

首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c;

然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,a[n] - c;

为啥还要打个补丁？

我们画个图理解一下这个公式的由来:

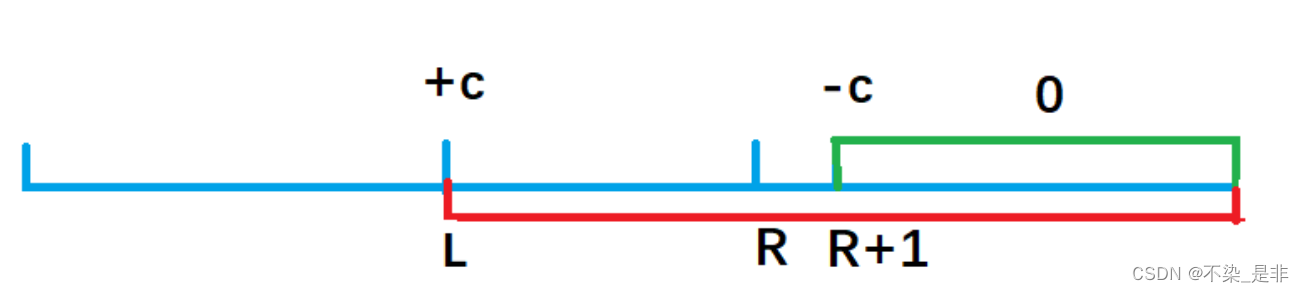
b[l] + c，效果使得a数组中 a[l]及以后的数都加上了c(红色部分)，但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

因此我们得出一维差分结论：给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。

差分数组加减完后，由公式b[i] = a[i] - a[i - 1] 逆推出 前缀和数组a[i] = b[i] + a[i - 1]

题目：差分

题目链接：差分

输入一个长度为 n的整数序列。接下来输入 m个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]之间的每个数加上 c。请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n和 m。
第二行包含 n个整数，表示整数序列。
接下来 m行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

代码及详细注释：

n, m = map(int, input().split())  # 输入两个整数n和m
a = list(map(int, input().split()))  # 输入n个整数，存储在列表a中
a = [0, *a]  # 在列表a的开头插入一个0
b = [0] * (n + 2)  # 初始化长度为n+2的全0列表b# 计算列表b中每个元素的值
for i in range(1, n + 1):b[i] = a[i] - a[i - 1]# 根据输入的操作更新列表b的值
for _ in range(m):l, r, c = map(int, input().split())b[l] += cif r != n: # 判断是否会出界，如果b数组定义的很长，则无需判断b[r + 1] -= c# 也可以这样写，但空间复杂度会高一点
# res = [0] * n
# res[0] = b[1]
# for i in range(2, n + 1):
#     res[i - 1] = b[i] + res[i - 2]
# print(" ".join(map(str, res)))# 计算最终结果
for i in range(1, n + 1):b[i] += b[i - 1]# 输出最终结果，去除首尾两个元素并将列表转换为字符串输出
print(' '.join(map(str, b[1:-1])))

总结：

前缀和&差分可以说是算法竞赛中必考的知识点，需要熟练掌握。
一维差分总结就两个公式：

1. b[l] + = c, b[r+1] - = c
2. b[i] = a[i] - a[i - 1]

这篇关于一维前缀和一维差分（下篇讲解二维前缀和二维差分）（超详细，python版，其他语言也很轻松能看懂）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---