本文主要是介绍深入电机控制基础知识(1)- 磁共能与电磁转矩,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.1 概述
打开任意一本电机学的教材,翻到电机基本概念的说明的位置,总能看到一句描述电机本质的话:电机是一种机电能量转化的装置。
机电能量转化,很生动形象的说明电机的工作原理。对于电动机而言,吸收电能,释放机械能,对于发电机而言,吸收机械能,转化为电能。在这个过程中,电机会产生电磁转矩。
那么大家有没有想过,为什么叫电磁转矩?电磁转矩又是怎么产生的呢?下面我就会从能量守恒的角度,推导一下电磁转矩产生的过程。
1.2 磁能
通电导体,会在周围产生磁场,而磁场能量分布在磁场所在的整个空间里面,记 w m w_m wm为单位体积中的磁能,也叫磁能密度,其可以表示为:
w m = 1 2 B H = 1 2 B 2 μ (1.1) \begin{equation} \begin{aligned} w_m=\frac{1}{2}BH=\frac{1}{2}\frac{B^2}{\mu} \end{aligned} \end{equation} \tag{1.1} wm=21BH=21μB2(1.1)
可以看的出来,磁导率越大的地方,储存的磁场能量越少。电机中铁芯的磁导率是远远大于空气的,因此电机中的能量,实际上都是集中在了气隙中的。

如果记气隙的体积为 V δ V_{\delta} Vδ,那么其中储存的能量可以表示为:
W m = 1 2 B δ 2 μ 0 V δ (1.2) \begin{equation} \begin{aligned} W_m=\frac{1}{2}\frac{B_{\delta}^{2}}{\mu _0}V_{\delta} \end{aligned} \end{equation} \tag{1.2} Wm=21μ0Bδ2Vδ(1.2)
1.3 机电能量转化装置
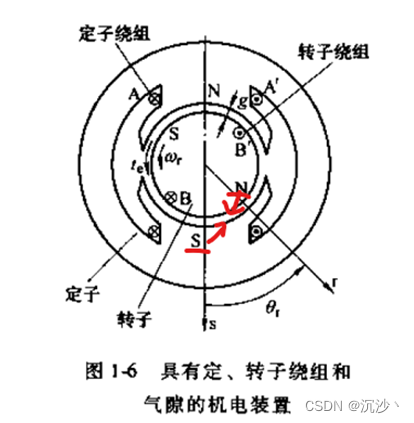
考虑如下的结构,线圈A和线圈B,分别接到电源上。线圈A作为定子绕组,其由两个线圈串联而成,总匝数为 N A N_A NA。线圈B位于一个可以旋转的转子中,其匝数为 N B N_B NB,定转子之间的单边气隙长度为 g g g,总气隙为 δ = 2 g \delta =2g δ=2g。
在忽略定转子铁芯此路中的磁阻(认为铁芯磁导率 μ F e = ∞ \mu _{Fe}=\infty μFe=∞)后,根据公式(1.1),可以得到此时通电线圈A和通电线圈B产生的磁场能量,全部储存于两个气隙中。
图 1 机电能量转化装置示意图
按照上图的电流、转矩方向定义。当电流 i A i_A iA为正时,根据右手定则,产生磁场方向为竖直向下,记此基波(正弦)磁场,磁感应强度幅值所在的方向为定子磁场轴线s。同理,当电流 i B i_B iB为正时,记产生径向基波磁场的轴线为转子绕组轴线r。取s轴为空间参考轴,电角度 θ r \theta _r θr为转子位置角,按照上述定义方向,记转子速度正方向为逆时针方向,电磁转矩的方向和转子转速正方向一致,也为逆时针。
1.4 电能计算
1.4.1 电能
记线圈A产生的全磁链为 ψ A \psi _A ψA,根据法拉第电磁感应定律, ψ A \psi _A ψA的变化将在线圈A中产生感应电动势 e A e_A eA。设 e A e_A eA的正方向和 i A i_A iA正方向一致, i A i_A iA方向与 ψ A \psi _A ψA方向符合右手螺旋定则,那么有:
e A = − d ψ A d t (1.3) \begin{equation} \begin{aligned} e_A=-\frac{d\psi _A}{dt} \end{aligned} \end{equation} \tag{1.3} eA=−dtdψA(1.3)
根据电路基尔霍夫第二定律,线圈A的电压可以表示为:
u A = R A i A − e A = R A i A + d ψ A d t (1.4) \begin{equation} \begin{aligned} u_A=R_Ai_A-e_A=R_Ai_A+\frac{d\psi _A}{dt} \end{aligned} \end{equation} \tag{1.4} uA=RAiA−eA=RAiA+dtdψA(1.4)
那么在时间 d t dt dt内,输入线圈A的净电能 d W e A A dW_{eAA} dWeAA为:
d W e A = u A i A d t − R A i A 2 d t = − e A i A d t = i A d ψ A (1.5) \begin{equation} \begin{aligned} dW_{eA}=u_Ai_Adt-R_Ai_{A}^{2}dt=-e_Ai_Adt=i_Ad\psi _A \end{aligned} \end{equation} \tag{1.5} dWeA=uAiAdt−RAiA2dt=−eAiAdt=iAdψA(1.5)
同理可得,在时间 d t dt dt内,输入线圈B的净电能 d W e B B dW_{eBB} dWeBB为:
d W e B = u B i B d t − R B i B 2 d t = − e B i B d t = i B d ψ B (1.6) \begin{equation} \begin{aligned} dW_{eB}=u_Bi_Bdt-R_Bi_{B}^{2}dt=-e_Bi_Bdt=i_Bd\psi _B \end{aligned} \end{equation} \tag{1.6} dWeB=uBiBdt−RBiB2dt=−eBiBdt=iBdψB(1.6)
因此当线圈A和线圈B中的电流同时变化时,在时间 d t dt dt内,由外部电源输入两者的净电能 d W e dW_e dWe为:
d W e = − ( e A i A + e B i B ) d t = i A d ψ A + i B d ψ B (1.7) \begin{equation} \begin{aligned} dW_e & =-\left( e_Ai_A+e_Bi_B \right) dt\\ & =i_Ad\psi _A+i_Bd\psi _B \end{aligned} \end{equation} \tag{1.7} dWe=−(eAiA+eBiB)dt=iAdψA+iBdψB(1.7)
1.4.2 电感
当线圈A中的励磁电流 i A i_A iA变化时,其产生的自感磁链 ψ A A \psi _{AA} ψAA将发生变化,同时由于线圈B产生的磁通要和线圈A交链,因此当线圈B中的励磁电流 i B i_B iB变化时,会在线圈A中产生互感磁链 ψ m A B \psi _{mAB} ψmAB。
对与线圈A产生的自感磁链 ψ A A \psi _{AA} ψAA,可以表示为:
ψ A A = ψ σ A + ψ m A = ( L σ A + L m A ) i A = L A i A (1.8) \begin{equation} \begin{aligned} \psi _{AA} & =\psi _{\sigma A}+\psi _{mA}\\ & =\left( L_{\sigma A}+L_{mA} \right) i_A\\ & =L_Ai_A \end{aligned} \end{equation} \tag{1.8} ψAA=ψσA+ψmA=(LσA+LmA)iA=LAiA(1.8)
其中: ψ σ A \psi _{\sigma A} ψσA为漏磁链(线圈A产生的没有穿过气隙由铁芯外空气闭合产生的磁场,与线圈A交链产生的漏磁连), ψ m A \psi _{mA} ψmA为自感磁链, L σ A L_{\sigma A} LσA为漏磁电感, L m A L_{mA} LmA为励磁自感 L A L_A LA为自感。
对于线圈B在线圈A中产生的互感磁链 ψ m A B \psi _{mAB} ψmAB,可以表示为:
ψ m A B = L A B ( θ r ) i B (1.9) \begin{equation} \begin{aligned} \psi _{mAB}=L_{AB}\left( \theta _r \right) i_B \end{aligned} \end{equation} \tag{1.9} ψmAB=LAB(θr)iB(1.9)
其中: L A B ( θ r ) L_{AB}\left( \theta _r \right) LAB(θr)为线圈A与线圈B之间的互感,其随着转子位置 θ r \theta _r θr改变而改变。
对于基波磁场可以表示为:
L A B ( θ r ) = M A B cos θ r (1.10) \begin{equation} \begin{aligned} L_{AB}\left( \theta _r \right) =M_{AB}\cos \theta _r \end{aligned} \end{equation} \tag{1.10} LAB(θr)=MABcosθr(1.10)
当 θ r = 0 \theta _r=0 θr=0,即绕组A和绕组B处于全耦合的状态下,两者的互感达到最大值 M A B M_{AB} MAB。
综上所述,绕组A中全磁链可以表示为:
ψ A = ψ A A + ψ m A B = L A i A + M A B cos θ r i B (1.11) \begin{equation} \begin{aligned} \psi _A & =\psi _{AA}+\psi _{mAB}\\ & =L_Ai_A+M_{AB}\cos \theta _ri_B \end{aligned} \end{equation} \tag{1.11} ψA=ψAA+ψmAB=LAiA+MABcosθriB(1.11)
同理可得,绕组B中全磁链可以表示为:
ψ B = ψ B B + ψ m B A = L B i B + M B A cos θ r i A (1.12) \begin{equation} \begin{aligned} \psi _B & =\psi _{BB}+\psi _{mBA}\\ & =L_Bi_B+M_{BA}\cos \theta _ri_A \end{aligned} \end{equation} \tag{1.12} ψB=ψBB+ψmBA=LBiB+MBAcosθriA(1.12)
1.5 磁能计算
假设图 1中的可转转子被固定住( θ r = C o n s t \theta _r=Const θr=Const),线圈A和线圈B之间互感为固定值,此时不产生机械能,在忽略漏磁场的情况下,输入的全部电能均转化为磁能,在这种情况下,磁能可以表示为:
d W m = d W e = i A d ψ A + i B d ψ B (1.13) \begin{equation} \begin{aligned} dW_m & =dW_e\\ & =i_Ad\psi _A+i_Bd\psi _B \end{aligned} \end{equation} \tag{1.13} dWm=dWe=iAdψA+iBdψB(1.13)
假设一开始两个绕组的磁链均为0,那么当两者的磁链分别增长到 ψ A \psi _A ψA和 ψ B \psi _B ψB时,整个电磁装置的磁场能量为:
W m ( ψ A , ψ B ) = ∫ 0 ψ A i A d ψ + ∫ 0 ψ B i B d ψ (1.14) \begin{equation} \begin{aligned} W_m\left( \psi _A,\psi _B \right) =\int_0^{\psi _A}{i_Ad\psi}+\int_0^{\psi _B}{i_Bd\psi} \end{aligned} \end{equation} \tag{1.14} Wm(ψA,ψB)=∫0ψAiAdψ+∫0ψBiBdψ(1.14)
上式表明,磁能 W m W_m Wm是关于磁链 ψ A , ψ B \psi _A,\psi _B ψA,ψB的函数。
在忽略漏磁场的情况下,线圈A中磁链和电流关系可以用下图表示:
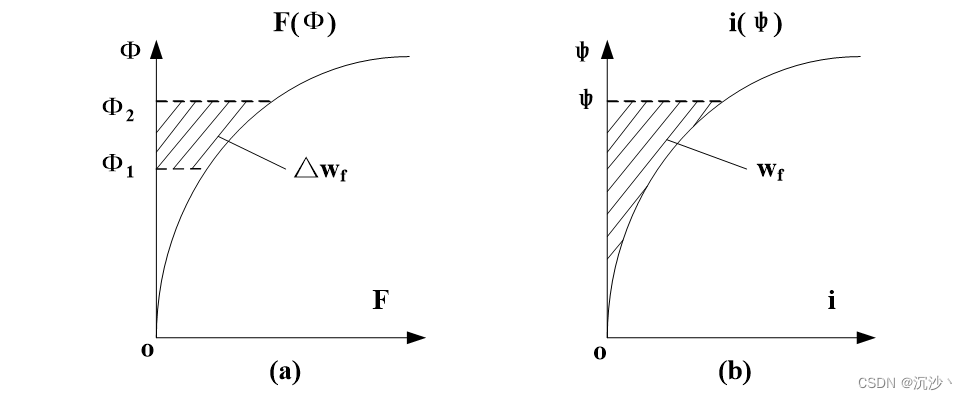
图 2磁路关系
注意,按照式(1.14)的表达式,其以磁链为自变量,对电流进行积分,因此对应上图中阴影部分面积。
如果以电流为自变量,对磁链进行积分,可以得到磁共能的表达式:
W m ′ ( i A , i B ) = ∫ 0 i A ψ A d i + ∫ 0 i B ψ B d i (1.15) \begin{equation} \begin{aligned} W_{m}^{'}\left( i_A,i_B \right) =\int_0^{i_A}{\psi _Adi}+\int_0^{i_B}{\psi _Bdi} \end{aligned} \end{equation} \tag{1.15} Wm′(iA,iB)=∫0iAψAdi+∫0iBψBdi(1.15)
上式表明,磁共能 W m ′ W_{m}^{'} Wm′是关于电流 i A , i B i_A,i_B iA,iB的函数。
可以证明,磁能和磁共能的和为:
W m + W m ′ = i A ψ A + i B ψ B (1.16) \begin{equation} \begin{aligned} W_m+W_{m}^{'}=i_A\psi _A+i_B\psi _B \end{aligned} \end{equation} \tag{1.16} Wm+Wm′=iAψA+iBψB(1.16)
上述推导中,通过将转子固定住,推导得到了磁能的表达式,此时磁能只和两个变量 ψ A , ψ B \psi _A,\psi _B ψA,ψB有关,但是如果转子可以自由旋转,由于 ψ A , ψ B \psi _A,\psi _B ψA,ψB本身与转子位置 θ r \theta _r θr相关,因此磁能的与三个变量 ψ A , ψ B , θ r \psi _A,\psi _B,\theta _r ψA,ψB,θr相关,表达为:
W m = W m ( ψ A , ψ B , θ r ) (1.17) \begin{equation} \begin{aligned} W_m=W_m\left( \psi _A,\psi _B,\theta _r \right) \end{aligned} \end{equation} \tag{1.17} Wm=Wm(ψA,ψB,θr)(1.17)
对上式求偏导,可以得到磁能增量的表达式:
d W m = ∂ W m ∂ ψ A d ψ A + ∂ W m ∂ ψ B d ψ B + ∂ W m ∂ θ r d θ r (1.18) \begin{equation} \begin{aligned} dW_m=\frac{\partial W_m}{\partial \psi _A}d\psi _A+\frac{\partial W_m}{\partial \psi _B}d\psi _B+\frac{\partial W_m}{\partial \theta _r}d\theta _r \end{aligned} \end{equation} \tag{1.18} dWm=∂ψA∂WmdψA+∂ψB∂WmdψB+∂θr∂Wmdθr(1.18)
根据式(1.13),可以得到:
d W m = i A d ψ A + i B d ψ B + ∂ W m ∂ θ r d θ r (1.19) \begin{equation} \begin{aligned} dW_m=i_Ad\psi _A+i_Bd\psi _B+\frac{\partial W_m}{\partial \theta _r}d\theta _r \end{aligned} \end{equation} \tag{1.19} dWm=iAdψA+iBdψB+∂θr∂Wmdθr(1.19)
与之类似的,可以得到磁共能的表达式:
d W m ′ = ψ A d i A + ψ B d i B + ∂ W m ′ ∂ θ r d θ r (1.20) \begin{equation} \begin{aligned} dW_{m}^{'}=\psi _Adi_A+\psi _Bdi_B+\frac{\partial W_{m}^{'}}{\partial \theta _r}d\theta _r \end{aligned} \end{equation} \tag{1.20} dWm′=ψAdiA+ψBdiB+∂θr∂Wm′dθr(1.20)
在忽略铁芯磁路磁阻的情况下,此时图 2中的 ψ − i \psi -i ψ−i关系就是一条直线,此时磁能和磁共能相等。而根据文献[1],在上述假设下可以得到上述所述的机电装置侧磁场储能可以表示为:
W m ′ = W m = 1 2 L A i A 2 + L A B ( θ r ) i A i B + 1 2 L B i B 2 (1.21) \begin{equation} \begin{aligned} W_{m}^{'}=W_m=\frac{1}{2}L_Ai_{A}^{2}+L_{AB}\left( \theta _r \right) i_Ai_B+\frac{1}{2}L_Bi_{B}^{2} \end{aligned} \end{equation} \tag{1.21} Wm′=Wm=21LAiA2+LAB(θr)iAiB+21LBiB2(1.21)
1.6 机电能量转化
在花费了很长的篇幅叙述电能和磁能分别是如何计算之后,终于来到了机电能量转化的部分。
记转子在时间 d t dt dt内,转过了一个微小的电角度 d θ r d\theta _r dθr,这会导致装置机械能发生变化,此过程相当于上述章节中推导磁能时,不将转子固定住。在这个过程中,系统从电源输入的电能转化为了两部分能量:磁能的变化量和机械能的变化量。
记此时转子上收到的电磁转矩为 t e t_e te,电磁转矩所做的功为:
d W m e c h = t e d θ r (1.22) \begin{equation} \begin{aligned} dW_{mech}=t_ed\theta _r \end{aligned} \end{equation} \tag{1.22} dWmech=tedθr(1.22)
根据能量守恒,有:
d W e = d W m + d W m e c h (1.23) \begin{equation} \begin{aligned} dW_e=dW_m+dW_{mech} \end{aligned} \end{equation} \tag{1.23} dWe=dWm+dWmech(1.23)
此时结合上述表达式,(1.7)(1.19)(1.22)(1.23),有:
t e d θ r = d W e − d W m = ( i A d ψ A + i B d ψ B ) − ( i A d ψ A + i B d ψ B + ∂ W m ∂ θ r d θ r ) = − ∂ W m ∂ θ r d θ r (1.24) \begin{equation} \begin{aligned} t_ed\theta _r & =dW_e-dW_m\\ & =\left( i_Ad\psi _A+i_Bd\psi _B \right) -\left( i_Ad\psi _A+i_Bd\psi _B+\frac{\partial W_m}{\partial \theta _r}d\theta _r \right) \\ & =-\frac{\partial W_m}{\partial \theta _r}d\theta _r \end{aligned} \end{equation} \tag{1.24} tedθr=dWe−dWm=(iAdψA+iBdψB)−(iAdψA+iBdψB+∂θr∂Wmdθr)=−∂θr∂Wmdθr(1.24)
进而可以得到电磁转矩的表达式为:
t e = − ∂ W m ( ψ A , ψ B , θ r ) ∂ θ r (1.25) \begin{equation} \begin{aligned} t_e=-\frac{\partial W_m\left( \psi _A,\psi _B,\theta _r \right)}{\partial \theta _r} \end{aligned} \end{equation} \tag{1.25} te=−∂θr∂Wm(ψA,ψB,θr)(1.25)
上述表达式是通过磁能表示的,转矩也可以用磁共能表示,根据(1.16)有:
t e d θ r = d W e − d W m = d W e − d ( i A ψ A + i B ψ B − W m ′ ) = ( i A d ψ A + i B d ψ B ) − ( i A d ψ A + i B d ψ B ) − ( ψ A d i A + ψ B d i B ) + d W m ′ = − ( ψ A d i A + ψ B d i B ) + d W m ′ = ∂ W m ′ ∂ θ r d θ r (1.26) \begin{equation} \begin{aligned} t_ed\theta _r & =dW_e-dW_m\\ & =dW_e-d\left( i_A\psi _A+i_B\psi _B-W_{m}^{'} \right) \\ & =\left( i_Ad\psi _A+i_Bd\psi _B \right) -\left( i_Ad\psi _A+i_Bd\psi _B \right) -\left( \psi _Adi_A+\psi _Bdi_B \right) +dW_{m}^{'}\\ & =-\left( \psi _Adi_A+\psi _Bdi_B \right) +dW_{m}^{'}\\ & =\frac{\partial W_{m}^{'}}{\partial \theta _r}d\theta _r \end{aligned} \end{equation} \tag{1.26} tedθr=dWe−dWm=dWe−d(iAψA+iBψB−Wm′)=(iAdψA+iBdψB)−(iAdψA+iBdψB)−(ψAdiA+ψBdiB)+dWm′=−(ψAdiA+ψBdiB)+dWm′=∂θr∂Wm′dθr(1.26)
进而得到:
t e = ∂ W m ′ ( i A , i B , θ r ) ∂ θ r (1.27) \begin{equation} \begin{aligned} t_e=\frac{\partial W_{m}^{'}\left( i_A,i_B,\theta _r \right)}{\partial \theta _r} \end{aligned} \end{equation} \tag{1.27} te=∂θr∂Wm′(iA,iB,θr)(1.27)
观察式(1.21),可以看出,使用磁共能计算电磁转矩更加简单,因此式(1.21)便是使用 i A , i B , θ r i_A,i_B,\theta _r iA,iB,θr作为自变量时磁能 W m W_m Wm和磁共能 W m ′ W_{m}^{'} Wm′的表达式。
将式(1.21)带入(1.27)得到:
t e = i A i B ∂ L A B ( θ r ) ∂ ( θ r ) = − i A i B M A B sin θ r (1.28) \begin{equation} \begin{aligned} t_e=i_Ai_B\frac{\partial L_{AB}\left( \theta _r \right)}{\partial \left( \theta _r \right)}=-i_Ai_BM_{AB}\sin \theta _r \end{aligned} \end{equation} \tag{1.28} te=iAiB∂(θr)∂LAB(θr)=−iAiBMABsinθr(1.28)
上式中的负号表示,对于图 1规定的正方向,在 i A , i B i_A,i_B iA,iB均为正值的情况下,此时产生的实际电磁转矩方向为顺时针方向,即使 θ r \theta _r θr减小的方向。
这个也是很好理解的,在上图的电流方向下,定子下边部分相当于S极,转子的下半部分相当于N极,NS极相互吸引,自然会使即使 θ r \theta _r θr减小。
这篇关于深入电机控制基础知识(1)- 磁共能与电磁转矩的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





