本文主要是介绍代码随想录算法训练营第二十五天|● 216.组合总和III ● 17.电话号码的字母组合(JS写法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
216 组合总和Ⅲ
题目链接/文章讲解:https://programmercarl.com/0216.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CIII.html
视频讲解:https://www.bilibili.com/video/BV1wg411873x

方法一:自己写的
自己写的,本题和77很像,就是在backTracking的终止条件里多加了一个条件,也就是sum===n
/*** @param {number} k* @param {number} n* @return {number[][]}*/
var combinationSum3 = function(k, n) {let res = [];let path = [];const backTracking = (n,k,start) => {let sum = 0;if(path.length === k){for(let j = 0;j< path.length;j++){sum += path[j];}if(sum === n){res.push([...path]);return;}}for(let i = start;i<=9;i++){path.push(i);backTracking(n,k,i+1);path.pop();}}backTracking(n,k,1);return res;
};
方法二:代码随想录的方法
把处理sum的逻辑放在了for循环里面,因此除了path要回溯,sum也要回溯
/*** @param {number} k* @param {number} n* @return {number[][]}*/
var combinationSum3 = function(k, n) {let res = [];let path = [];let sum = 0;const backTracking = (start,path) => {//终止条件//剪枝if (sum > n){return;}if(path.length === k){if(sum === n){res.push([...path]);//使用return,一旦找到正确的结果,就结束当前的递归分支return;}}//单层逻辑for(let i = start;i<=9-(k-path.length) + 1;i++){sum += i;path.push(i);backTracking(i+1,path);path.pop();//回溯sum -= i;}}backTracking(1,path);return res;};
17 电话号码的字母组合
题目链接/文章讲解:https://programmercarl.com/0017.%E7%94%B5%E8%AF%9D%E5%8F%B7%E7%A0%81%E7%9A%84%E5%AD%97%E6%AF%8D%E7%BB%84%E5%90%88.html
视频讲解:https://www.bilibili.com/video/BV1yV4y1V7Ug

/*** @param {string} digits* @return {string[]}*/
var letterCombinations = function(digits) {//digits的长度,就是树的深度const k = digits.length;//该数组对应0,1,2,3,4,5,6,7,8,9const map = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];//处理两种特殊情况if(!k) return [];if(k === 1) return map[digits].split("");let path = [];let res = [];//k不作为参数传递也可以const backTracking = (str,k,index) => {//终止条件//k既是树的深度,也是正确结果的长度if(path.length === k){res.push(path.join(""));return;}//str[index],假设digits="23",则第一轮str[index]=2//map[str[index]],map[2]="abc"//v就是依次取a,b,cfor(const v of map[str[index]]){path.push(v);backTracking(str,k,index+1);path.pop();}}backTracking(digits,k,0);return res;
};
注意!k和k===null的区别
if(!k):这个条件判断语句会在 k 的值为假值的情况下执行。在 JavaScript 中,以下值被视为假值(Falsy value):
false
0
‘’(空字符串)
null
undefined
NaN
因此,if(!k) 会在 k 的值为假值时执行代码块,其中包括当 k 为 0 或空字符串 ‘’ 的情况。
if(k === null):这个条件判断语句会严格检查 k 的值是否为 null。如果 k 不是 null,则条件不满足,代码块不会执行。
在考虑代码逻辑时,根据实际情况选择合适的条件判断形式很重要。在提供的代码中,digits 是一个字符串,而 map 中的每个对应项都是包含字母的字符串。因此,用 if(!k) 来判断 digits 的长度是否为 0 是合适的,因为 k 代表了 digits 字符串的长度,而 k 为 0 时表示没有输入数字,因此应该返回空数组 []。使用 if(k === null) 则无法正确捕捉到 k 为 0 的情况。
思路
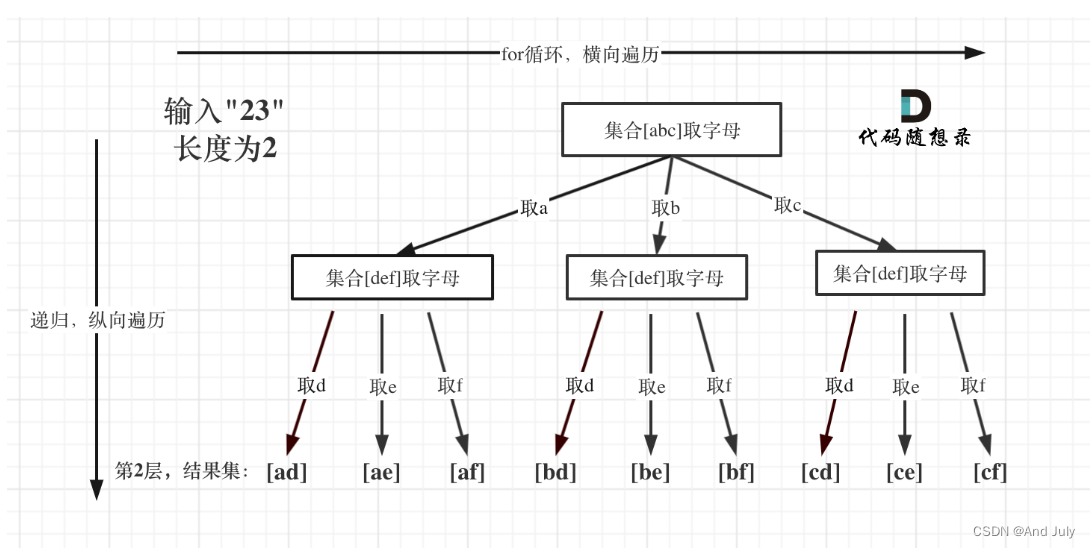
图中可以看出遍历的深度(之前的两道题,都是题干提供了规定的长度,可能是k什么的,本题没有明确说明,因此需要自己想象出树的结构,知道digits的长度就是遍历的深度),就是输入"23"的长度,而叶子节点就是我们要收集的结果。
k也是最后结果的长度
注意这个index可不是 77.组合 (opens new window)和216.组合总和III (opens new window)中的startIndex了。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
这篇关于代码随想录算法训练营第二十五天|● 216.组合总和III ● 17.电话号码的字母组合(JS写法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






