FCN 全卷积网络和转置卷积

本文主要是介绍FCN 全卷积网络和转置卷积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

今天来看一篇复古的文章，Full Convolutional Networks 即全卷积神经网络，这是 2015 年的一篇语义分割方向的文章，是一篇比较久远的开山之作。因为最近在研究语义分割方向，所以还是决定先从这个鼻祖入手，毕竟后面的文章很多都借鉴了这篇文章的思想，掌握好基础我们才能飞的更高。本篇文章分为两部分: 论文解读与代码实现。

论文地址:

Fully Convolutional Networks for Semantic Segmentation​people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf

论文解读

• 语义分割介绍

语义分割(Semantic Segmentation)的目的是对图像中每一个像素点进行分类，与普通的分类任务只输出某个类别不同，语义分割任务输出是与输入图像大小相同的图像，输出图像的每个像素对应了输入图像每个像素的类别。

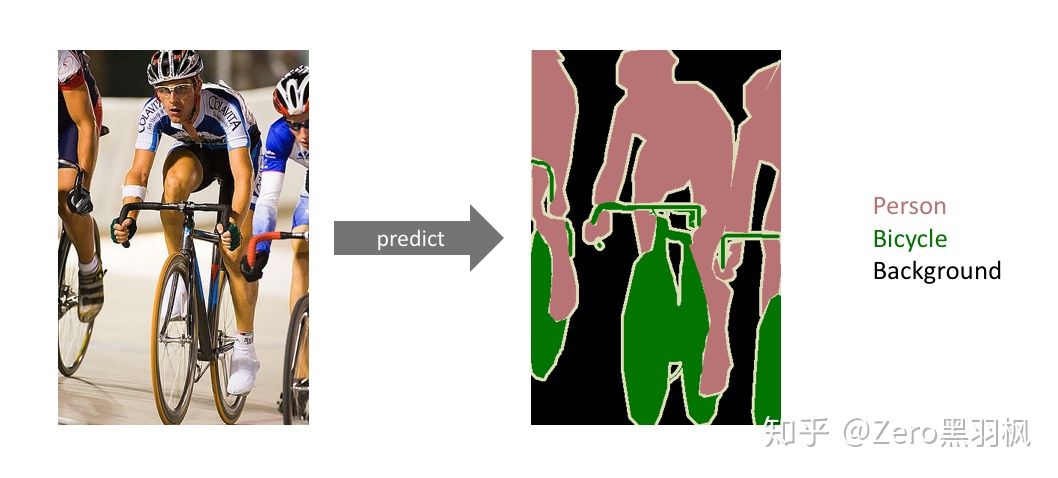
语义分割的预测结果

• 网络结构

FCN 的基本结构很简单，就是全部由卷积层组成的网络。用于图像分类的网络一般结构是"卷积-池化-卷积-池化-全连接"，其中卷积和全连接层是有参数的，池化则没有参数。论文作者认为全连接层让目标的位置信息消失了，只保留了语义信息，因此将全连接操作更换为卷积操作可以同时保留位置信息及语义信息，达到给每个像素分类的目的。网络的基本结构如下:

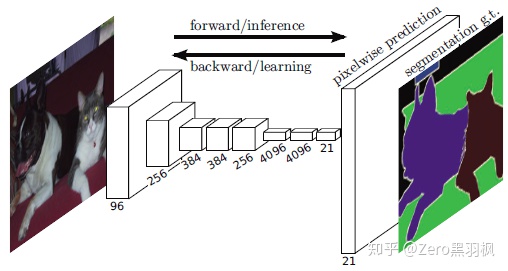
fcn网络结构

输入图像经过卷积和池化之后，得到的 feature map 宽高相对原图缩小了数倍，例如下图中，提取特征之后"特征长方体"的宽高为原图像的 1/32，为了得到与原图大小一致的输出结果，需要对其进行上采样(upsampling)，下面介绍上采样的方法之一-反卷积(图中最终输出的"厚度"是 21，因为类别数是 21，每一层可以看做是原图像中的每个像素属于某类别的概率，coding 的时候需要注意一下)。

网络结构细节

• 反卷积

反卷积是上采样(unsampling) 的一种方式，论文作者在实验之后发现反卷积相较于其他上采样方式例如 bilinear upsampling 效率更高，所以采用了这种方式。

关于反卷积的解释借鉴了这一篇: https://medium.com/activating-robotic-minds/up-sampling-with-transposed-convolution-9ae4f2df52d0， 英文OK的小伙伴推荐看原文，讲的很通透。

先看看正向卷积，我们知道卷积操作本质就是矩阵相乘再相加。现在假设我们有一个 4x4 的矩阵，卷积核大小为 3x3，步幅为 1 且不填充，那么其输出会是一个 2x2 的矩阵，这个过程实际是一个多对一的映射:

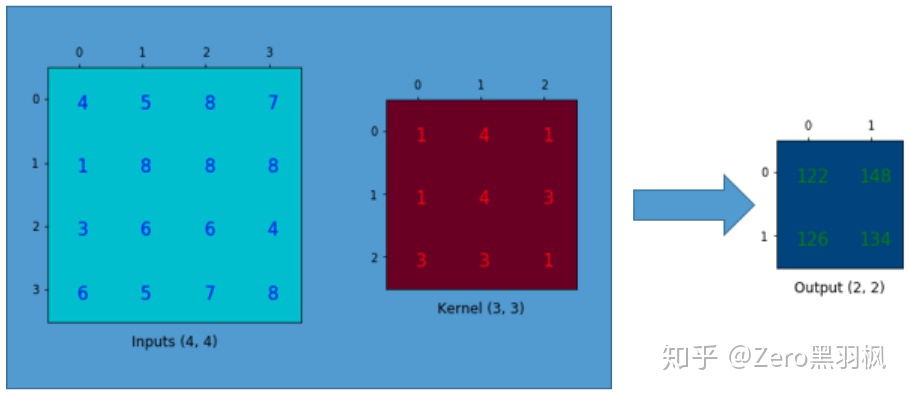
卷积

将整个卷积步骤分成四步来看是这样的过程:

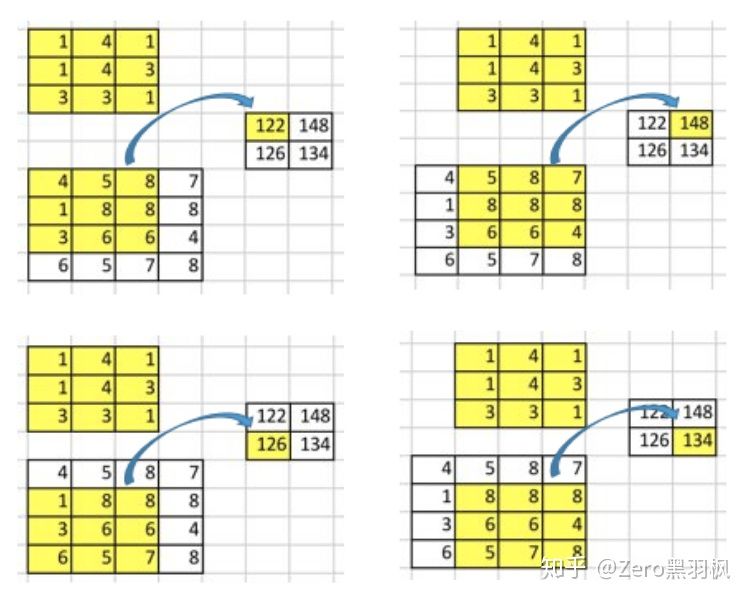
卷积步骤

从上图也可以看出，卷积操作其实是保留了位置信息的，例如输出矩阵中左上角的数字"122"就对应了原矩阵左上方的 9 个元素。

那么如何将结果的 2x2 的矩阵"扩展"为 4x4 的矩阵呢(一对多的映射)。我们从另一个角度来看卷积，首先我们将卷积核展开为一行，原矩阵展开为一列:

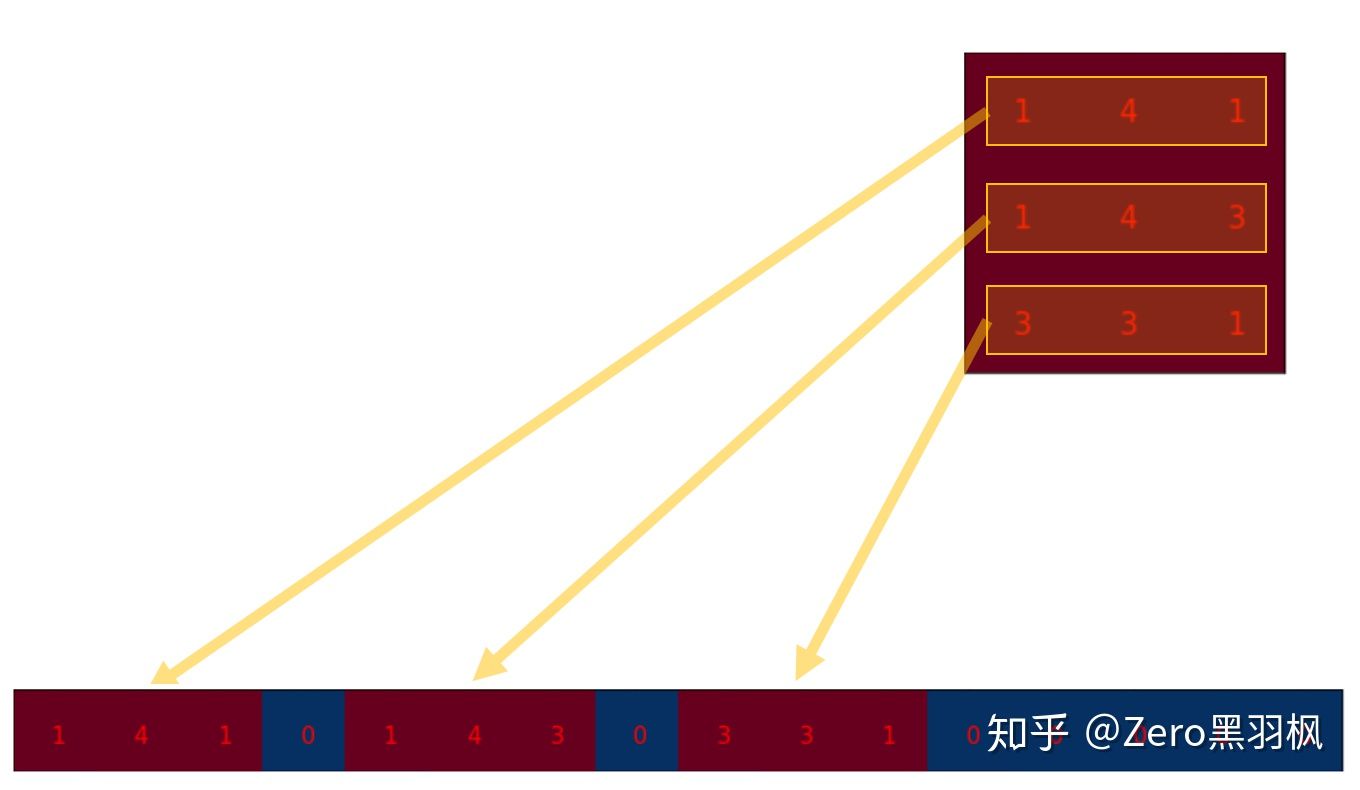
卷积核展开为一行

原矩阵展开为一列

则卷积过程的第一步:

卷积的第一个步骤

不要着急，可以细细体会一下，卷积操作确实如此。可以看出，4x16 的卷积核矩阵与 16x1 的输入矩阵相乘，得到了 4x1 的输出矩阵，达到了多对一映射的效果，那么将卷积核矩阵转置为 16x4 乘上输出矩阵 4x1 就可以达到一对多映射的效果，因此反卷积也叫做转置卷积。具体过程如下:

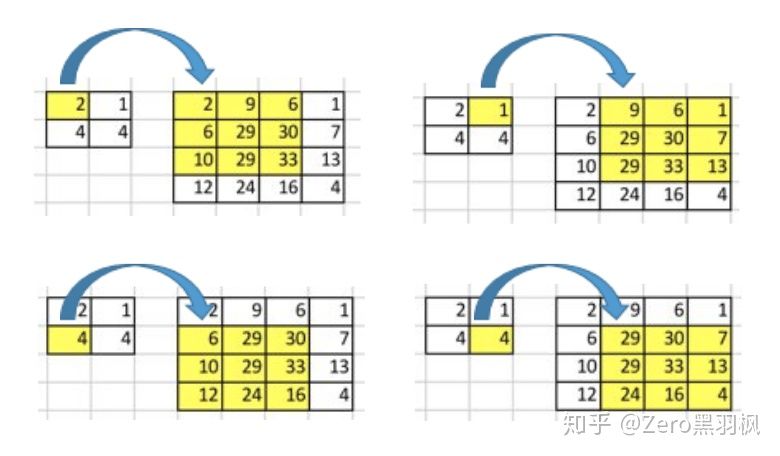
一对多

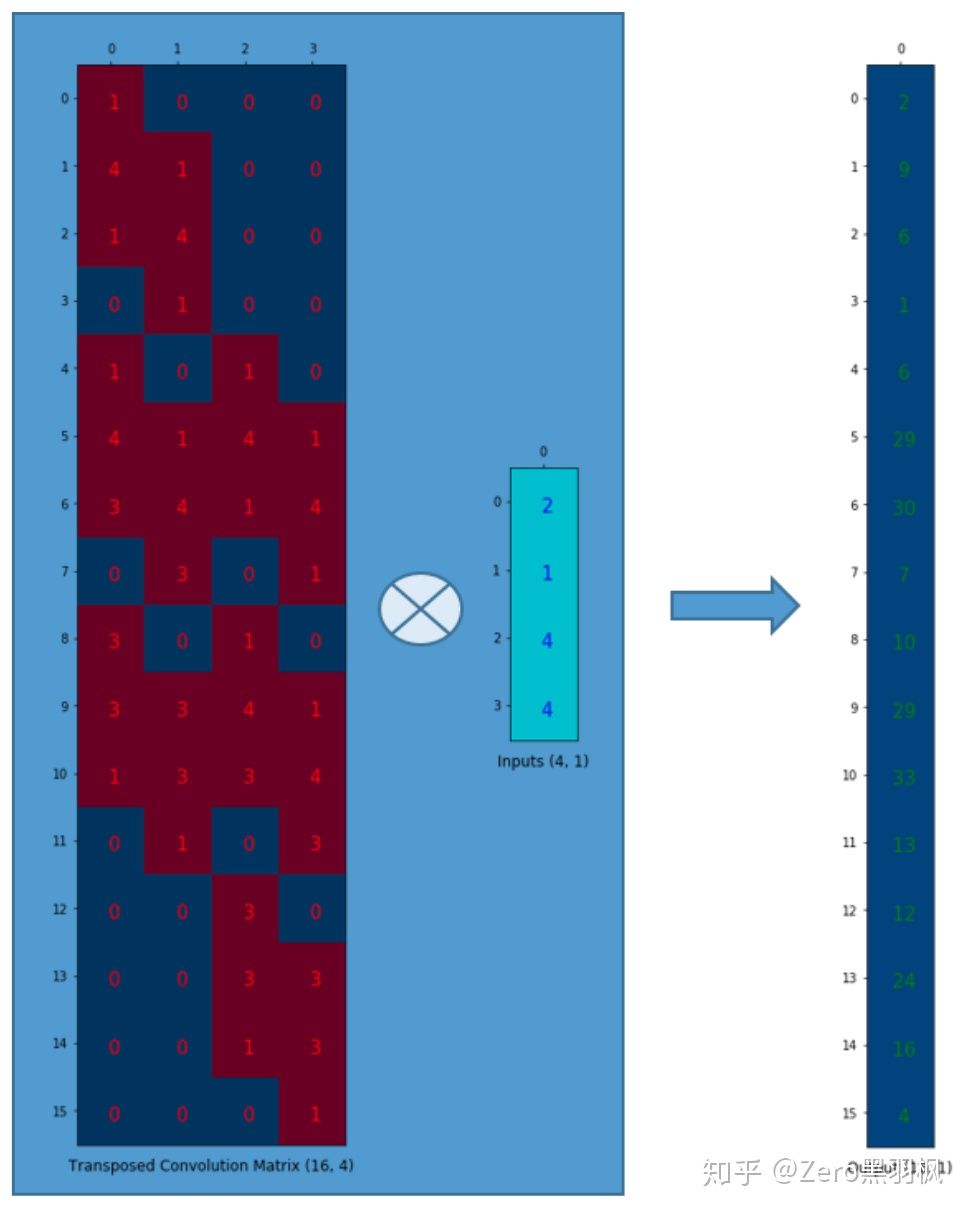
转置卷积

总结来说，全卷积网络的基本结构就是"卷积-反卷积-分类器"，通过卷积提取位置信息及语义信息，通过反卷积上采样至原图像大小，再加上深层特征与浅层特征的融合，达到了语义分割的目的。

------------------------------下面关于转置卷积的细节----------------------------

之间进行普通卷积的结果。

对应于下面的图像（这里的卷积核大小和举例不一样）：

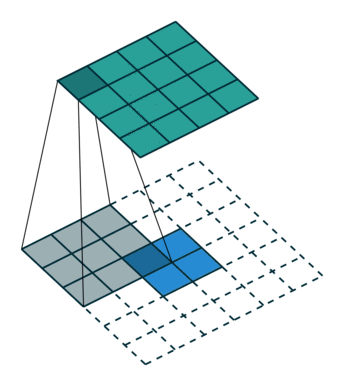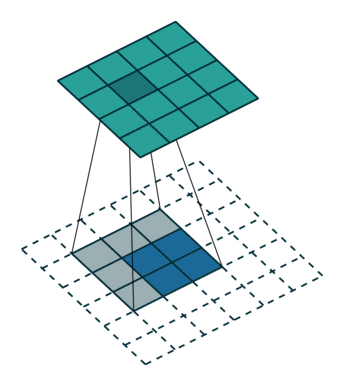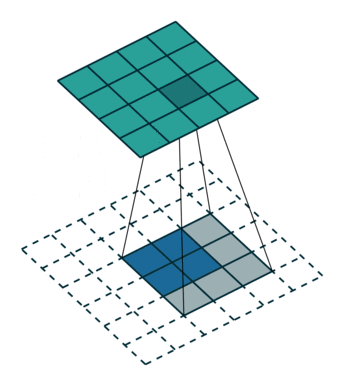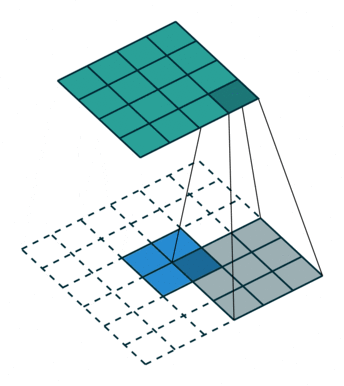
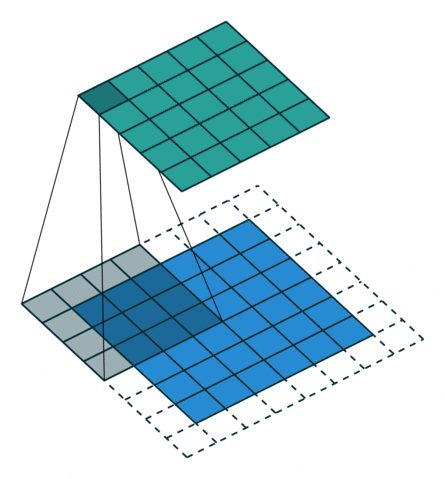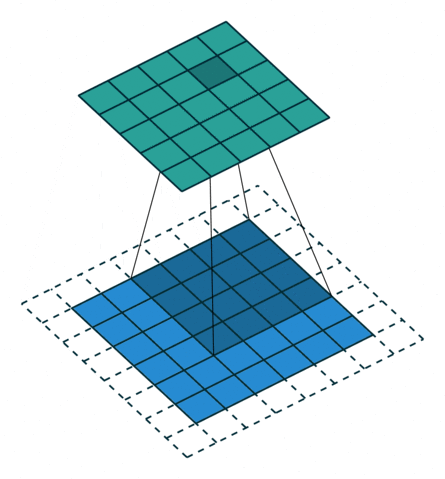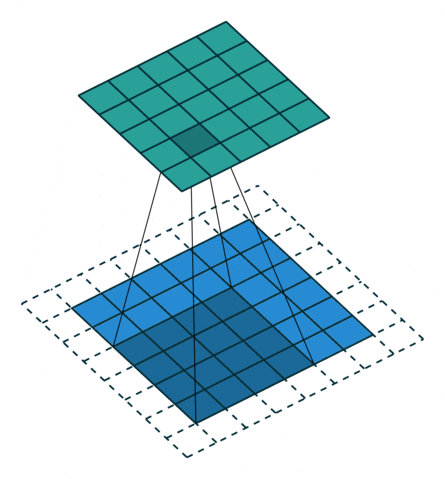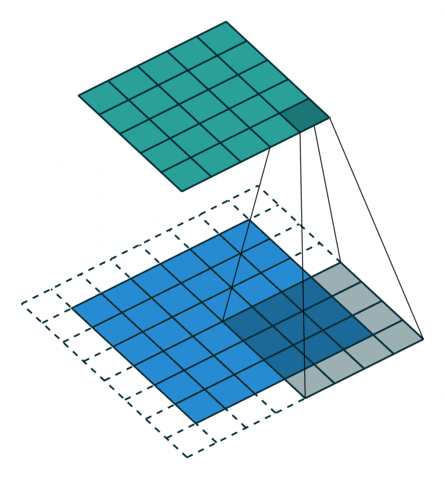
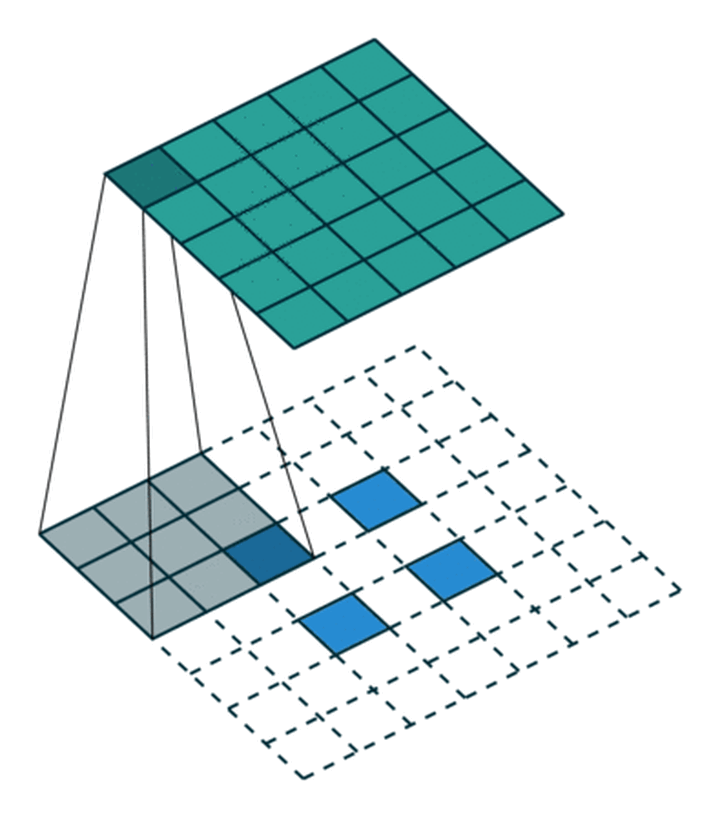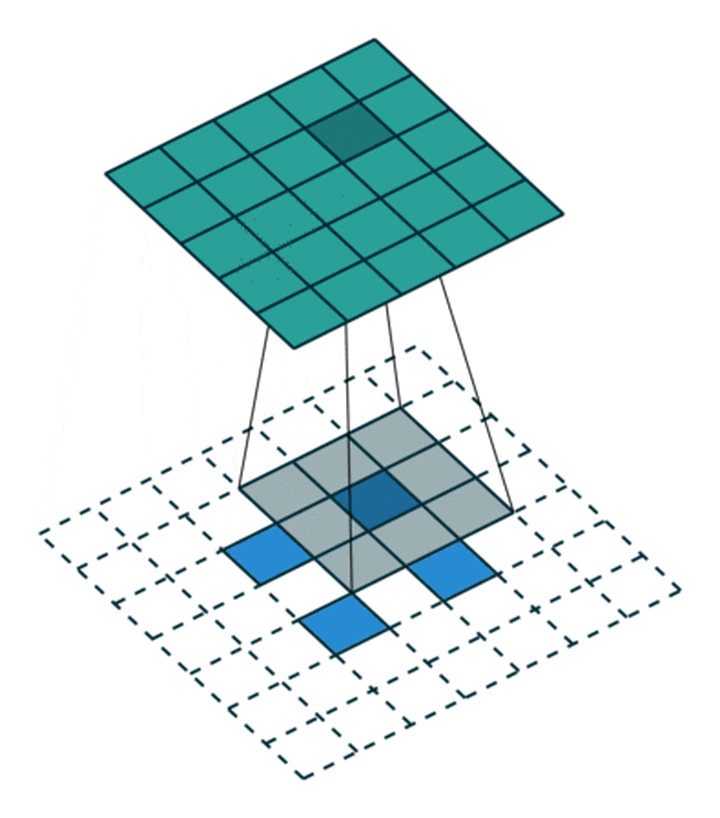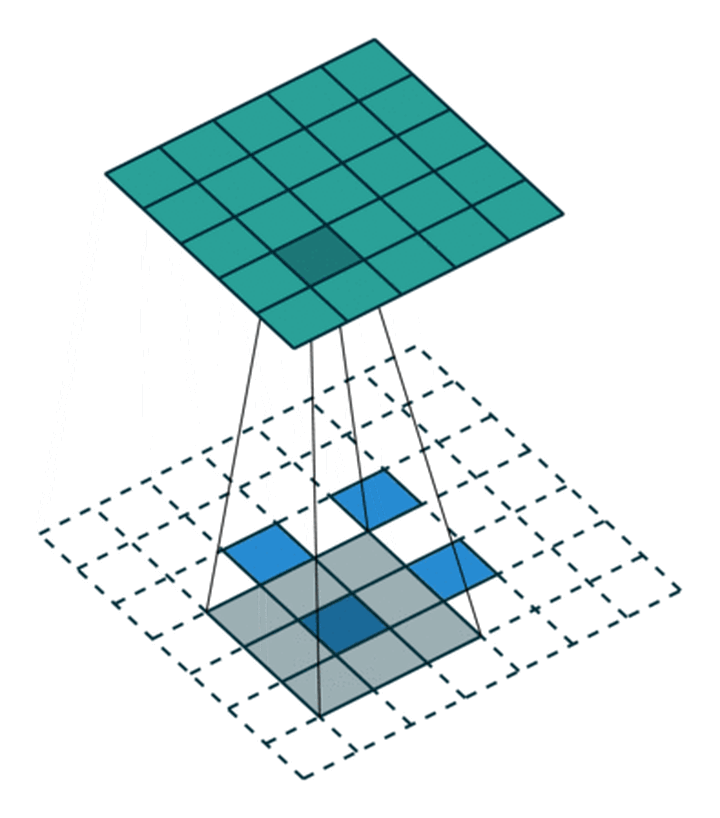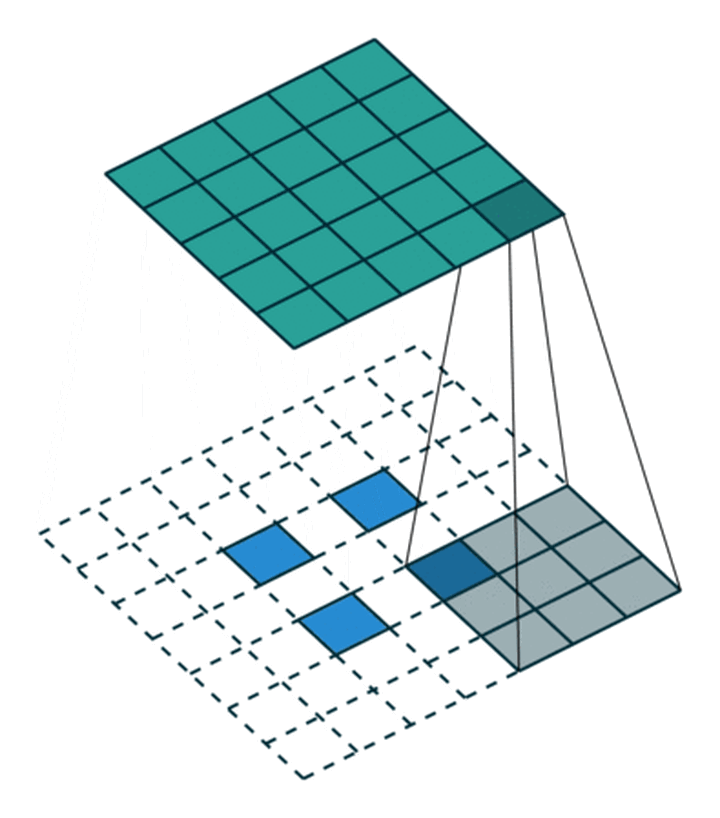
同样等价于输入添加空洞，额外padding，卷积核水平竖直翻转的普通卷积：

对应的gif图像：

公式计算

总结

实际使用时，stride>1的情况比较多，可以得到较大的上采样倍率，padding个人觉得没必要仔细研究，先转置卷积得到一个大分辨率的图像，再通过center crop，同样可以精确地恢复尺寸。

------------------------------------------

以下是反卷积是如何实现的，简单来说：

1. 卷积是Y=CX，反卷积就是Y=XC

2. 卷积和反卷积在数值上不一致，但是在shape上是可逆的

import torch
import torch.nn.functional as FX = torch.Tensor([[[[0,1,2,3],[4,5,6,7],[8,9,10,11],[12,13,14,15]]]])
C = torch.Tensor([[[[0,1,2],[3,4,5],[6,7,8]]]])
Y = F.conv2d(X, C)
print(Y)>>tensor([[[[258., 294.],[402., 438.]]]])

 

import torch
import torch.nn.functional as FX = torch.Tensor([[[[1,2],[3,4]]]])
C = torch.Tensor([[[[5,6],[7,8]]]])
Y = F.conv_transpose2d(X, C, stride=2,padding=0)
print(Y)>>tensor([[[[ 5.,  10.,  6.,  12.],[ 15.,  20.,  18.,  24.],[ 7.,  14.,  8.,  16.],[ 21., 28., 24., 32.]]]])

import torch
import torch.nn.functional as FX = torch.Tensor([[[[1,2],[3,4]]]])
C = torch.Tensor([[[[5,6],[7,8]]]])
Y = F.conv_transpose2d(X, C, stride=1,padding=0)
print(Y)>>tensor([[[[ 5., 16., 12.],[22., 60., 40.],[21., 52., 32.]]]])

 

import torch
import torch.nn.functional as FX = torch.Tensor([[[[1,2],[3,4]]]])
C = torch.Tensor([[[[5,6],[7,8]]]])
Y = F.conv_transpose2d(X, C, stride=1,padding=1)
print(Y)>>tensor([[[[60.]]]])

 from： 转置卷积(Transpose Convolution) - 知乎

手推反卷积 - 知乎

这篇关于FCN 全卷积网络和转置卷积的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---