程函方程伴随状态法走时层析，初至及反射

2024-03-17 08:50
文章标签 方程 状态 反射 伴随 层析 程函 初至 走时

本文主要是介绍程函方程伴随状态法走时层析，初至及反射，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

该方法最初由Sei和Symes在1994年提出，Leung and Qian (2006)的文章有较细致的阐述，Taillandier(2009)又将该方法整理发表到地球物理权威期刊Geophysics上。国内由本人所在的课题组的谢春，刘玉柱，董良国教授等人在2014年引入，2017年李勇德、刘玉柱和董良国教授等人提出了预条件伴随状态法走时层析方法发表在地球物理学报上（该预条件方法后来由Hu等人（2021）重新实验证明，以射线照明补偿为题，发表在Geophysics上）。之后勘探和天然地震领域的应用逐渐展开。2021年本人课题组再度发文，提出了不依赖于地表法向的改进伴随初至走时层析方法，随后将该方法应用在VTI初至走时反演和反射波走时反演中。

反射伴随走时层析的方法最初由Huang等人2012年提出发表于JGI上，存在的反射界面定位问题未解决。本人针对反射界面定位和反射走时拾取两个问题于2023和2024年分别在GP和Geophysics期刊上发表文章进行阐述，提出了面向实际地震勘探的ASCRT方法，将该方法推向实际地震勘探的应用中。详见

1. 透反射联合预条件走时层析

(PDF) Preconditioned transmission + reflection joint traveltime tomography with adjoint‐state method for subsurface velocity model building (researchgate.net)

2. 程函方程特征反射走时层析

(PDF) Eikonal-equation-based characteristic reflection traveltime tomography (researchgate.net)

3. 改进的初至伴随走时层析方法

(PDF) The improved first-arrival traveltime tomography based on the adjoint-state method (researchgate.net)

4. 改进的初至伴随走时层析方法在VTI反演中的应用（施加预条件照明补偿）

Illumination compensation for the adjoint-state first-arrival traveltime tomography in VTI media | Request PDF (researchgate.net)

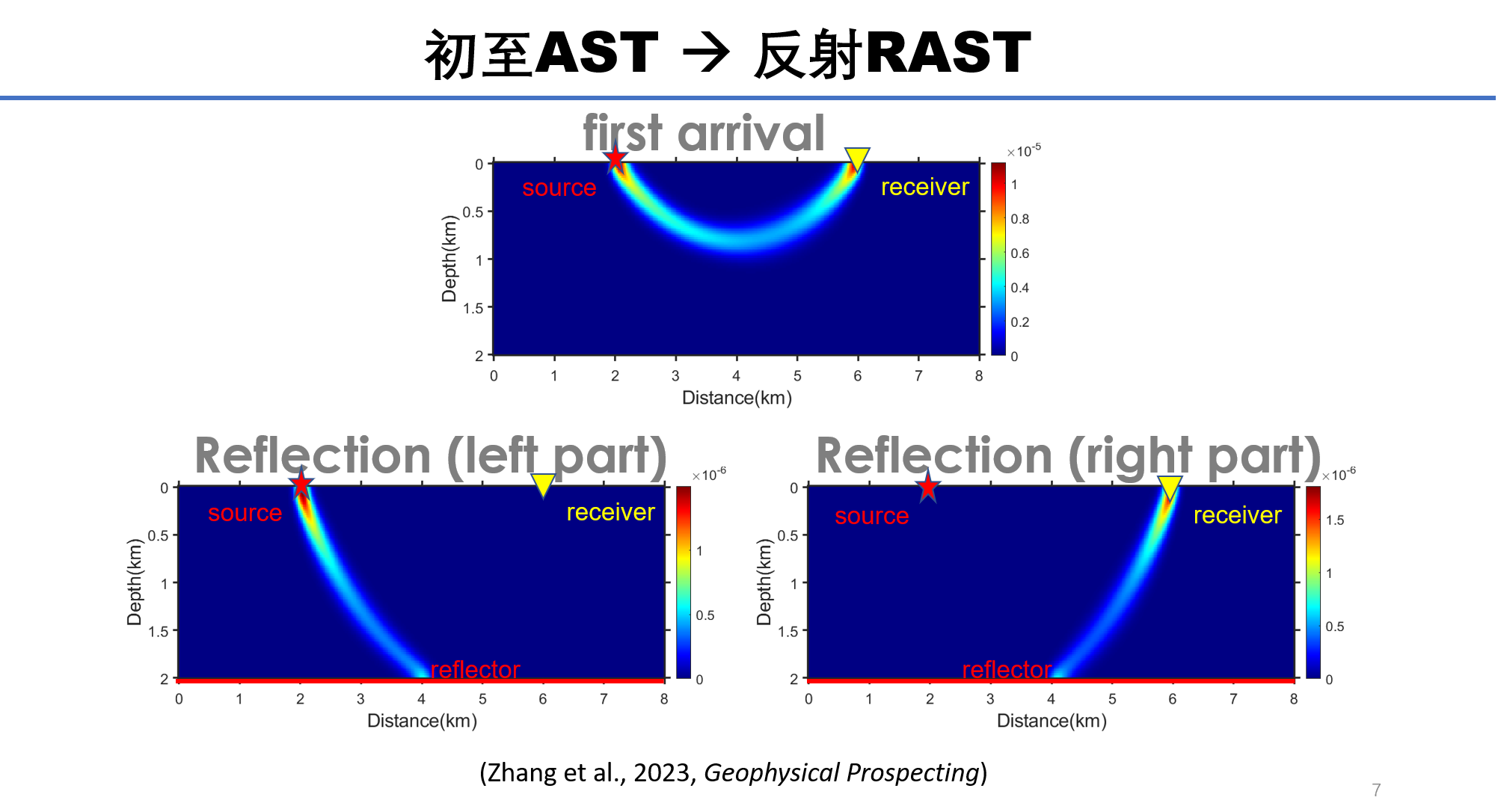
先给一个初至反演的理论模型例子：

真实模型和初始模型如上，初至走时反演结果如下

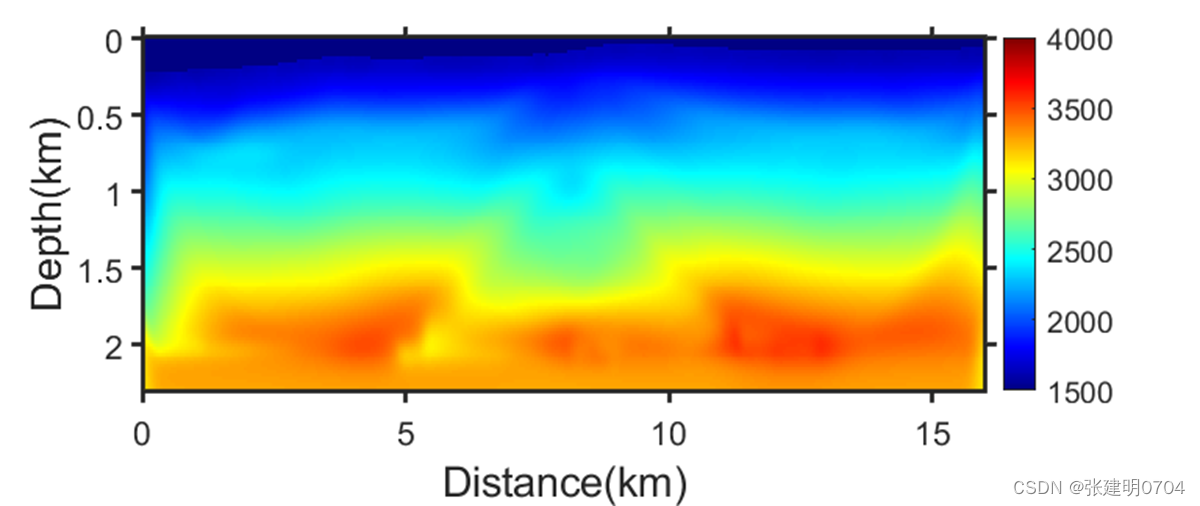
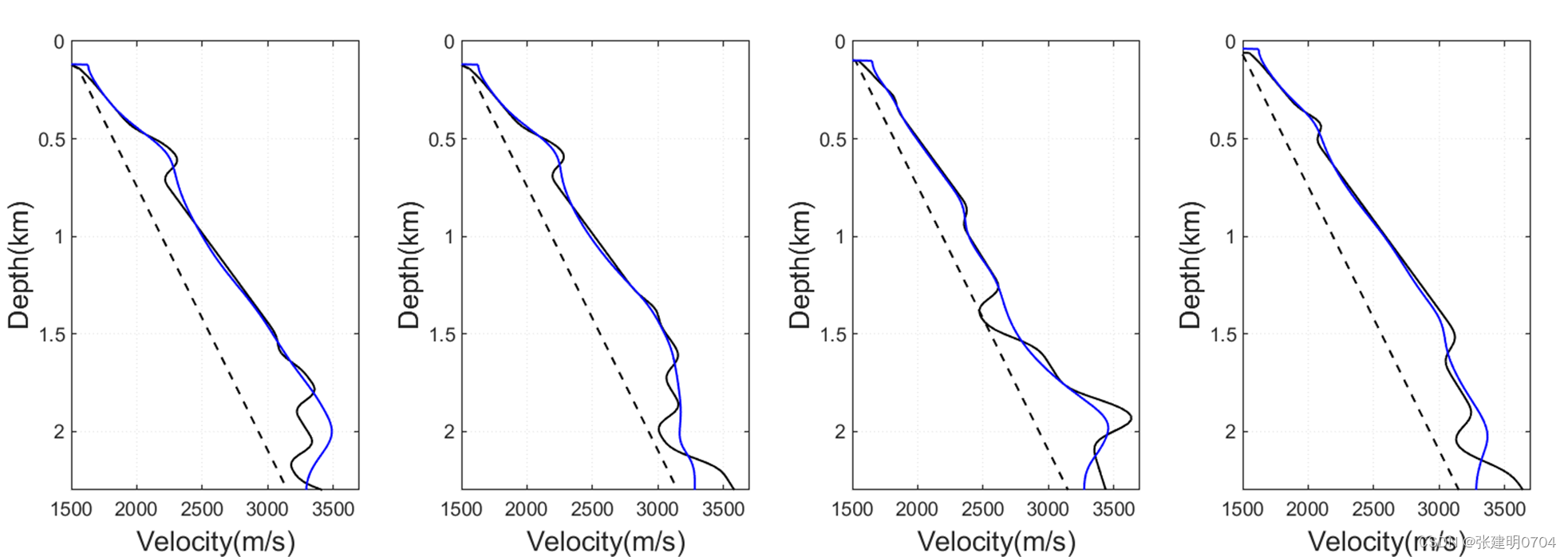
再给一个反射走时层剥离反演的理论模型例子：

实际资料反射走时层剥离反演例子：

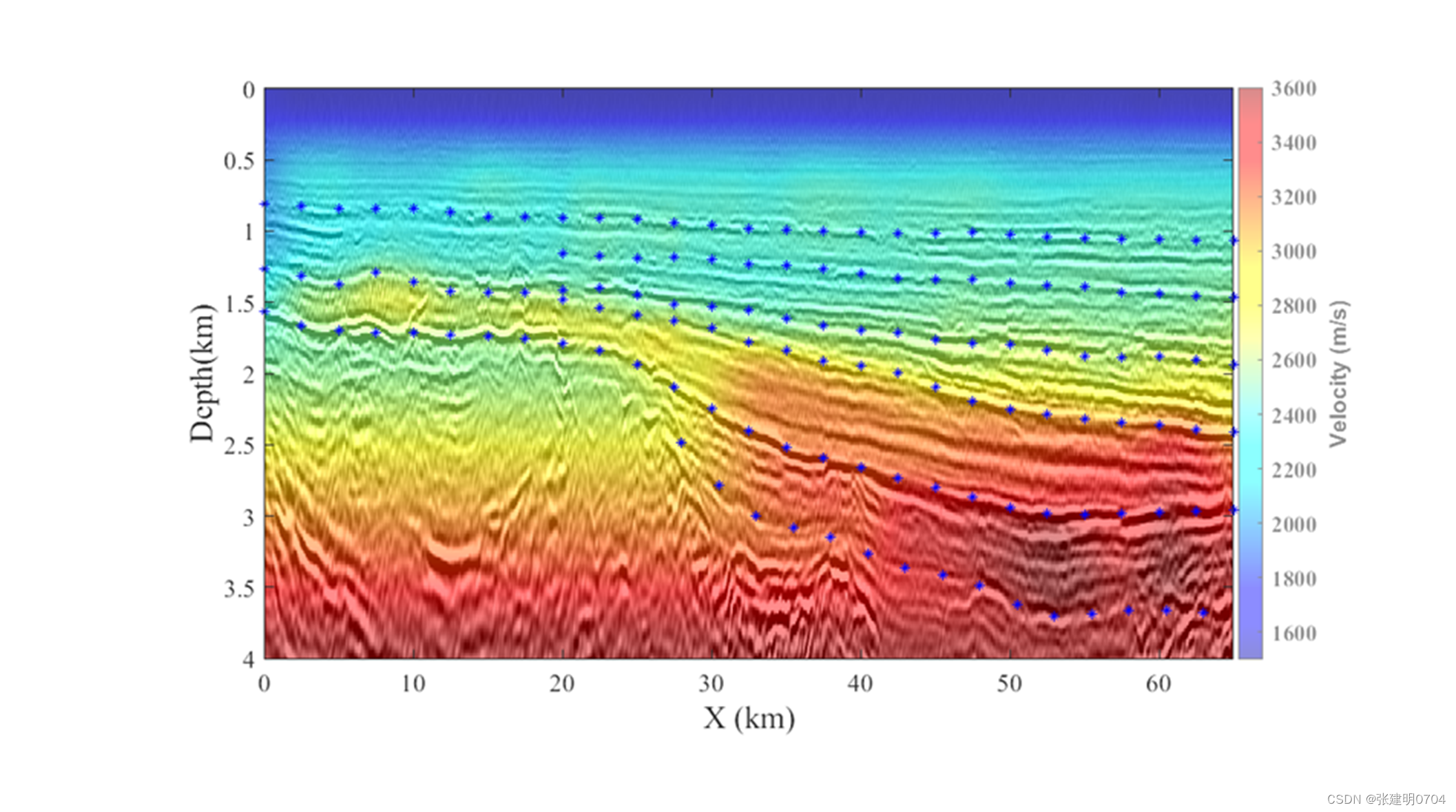
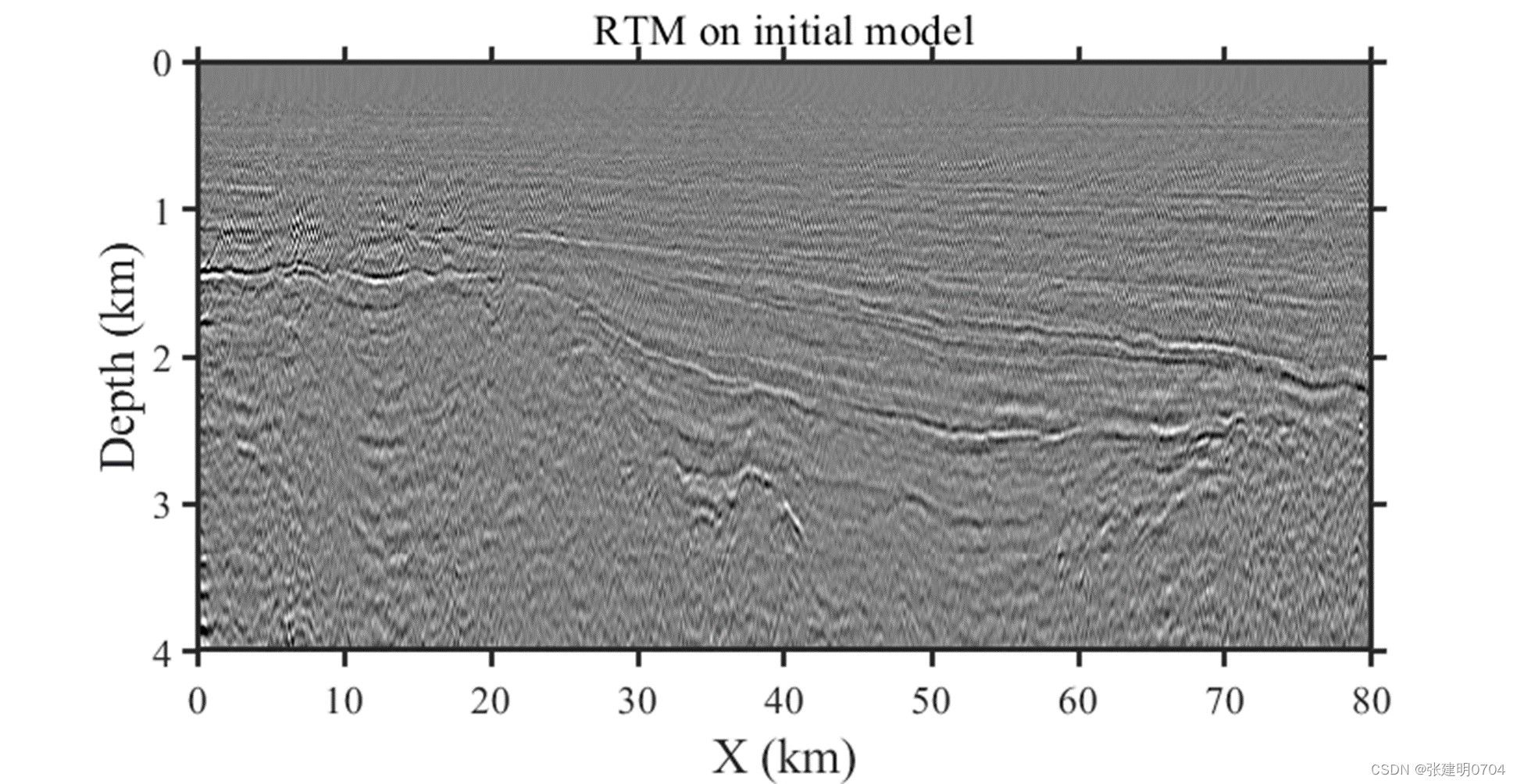
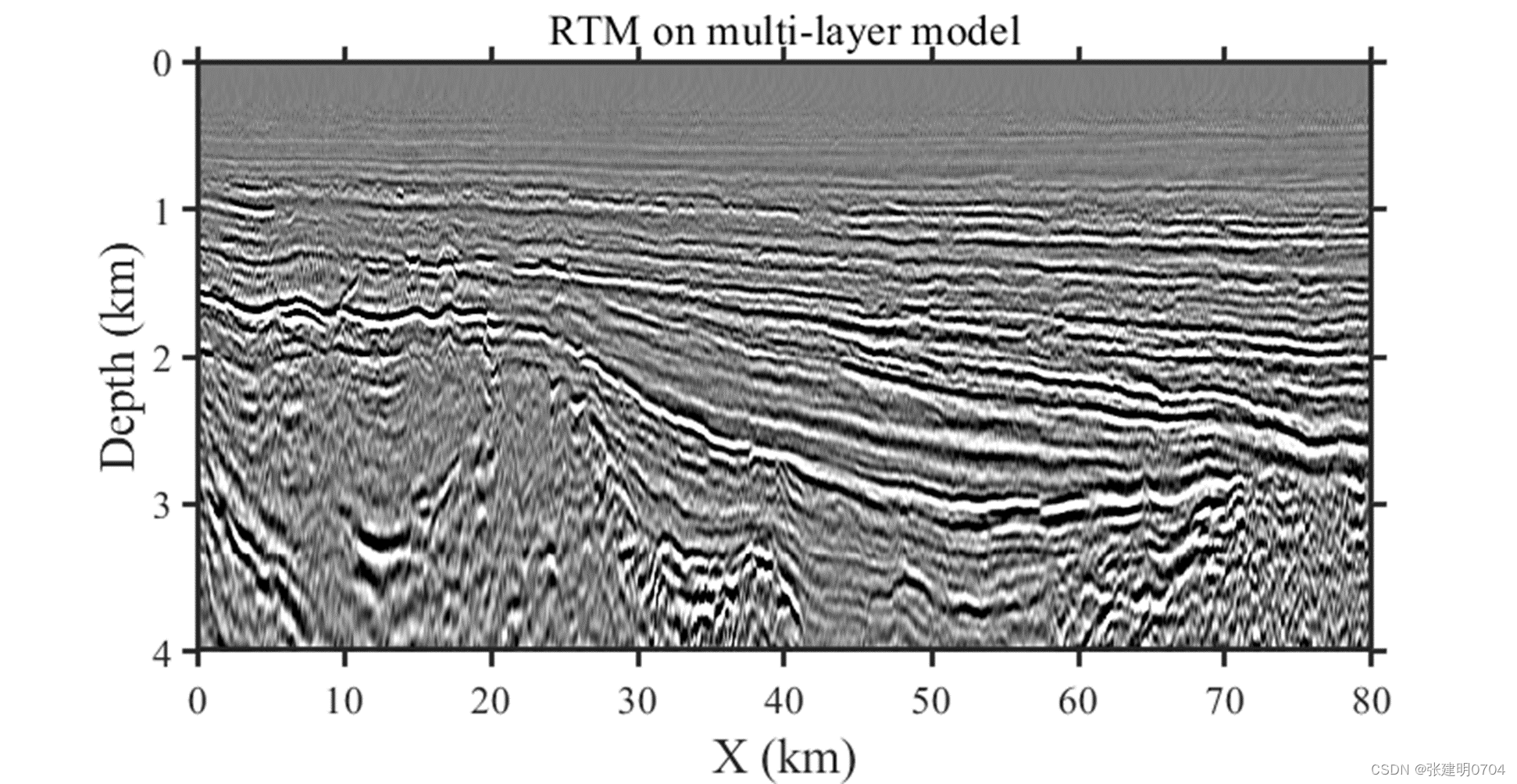
下图给出波动方程特征反射走时层析（WCRT）和程函方程伴随状态法特征反射走时层析（ASCRT）的效率和内存消耗对比：

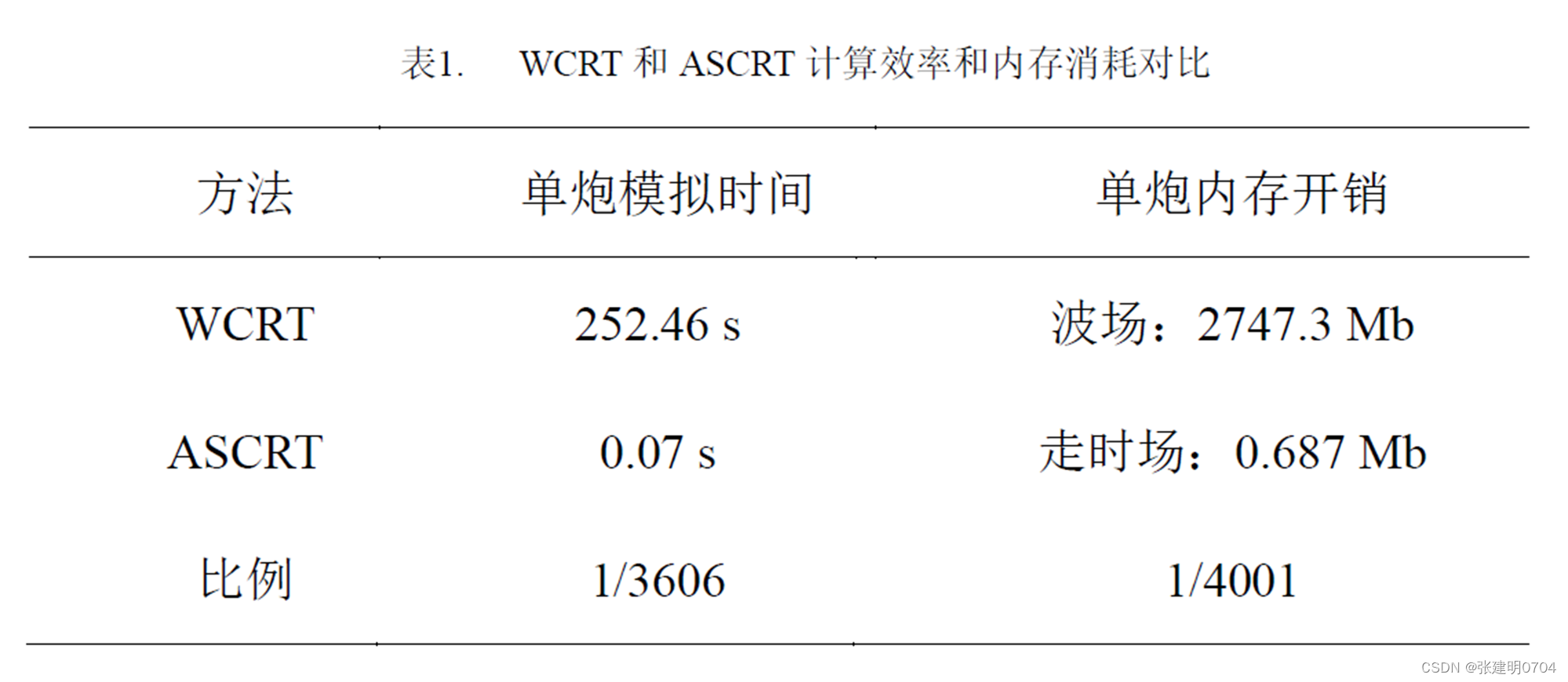
这篇关于程函方程伴随状态法走时层析，初至及反射的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/818460。

相关文章

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

利用康拓展开将一个排列映射成一个自然数，然后就变成了普通的广搜题。 #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#inclu
阅读更多...
hdu1565（状态压缩）

hdu1565（状态压缩）

本人第一道ac的状态压缩dp，这题的数据非常水，很容易过 题意：在n*n的矩阵中选数字使得不存在任意两个数字相邻，求最大值 解题思路： 一、因为在1<<20中有很多状态是无效的，所以第一步是选择有效状态，存到cnt[]数组中 二、dp[i][j]表示到第i行的状态cnt[j]所能得到的最大值，状态转移方程dp[i][j] = max(dp[i][j],dp[i-1][k]) ,其中k满足c
阅读更多...
【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂 关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】 嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。 正如翻译机将一种语言
阅读更多...
状态dp总结

状态dp总结

zoj 3631  N 个数中选若干数和（只能选一次）<=M 的最大值 const int Max_N = 38 ;int a[1<<16] , b[1<<16] , x[Max_N] , e[Max_N] ;void GetNum(int g[] , int n , int s[] , int &m){ int i , j , t ;m = 0 ;for(i = 0 ;
阅读更多...
hdu3006状态dp

hdu3006状态dp

给你n个集合。集合中均为数字且数字的范围在[1,m]内。m<=14。现在问用这些集合能组成多少个集合自己本身也算。 import java.io.BufferedInputStream;import java.io.BufferedReader;import java.io.IOException;import java.io.InputStream;import java.io.Inp
阅读更多...
从状态管理到性能优化：全面解析 Android Compose

从状态管理到性能优化：全面解析 Android Compose

文章目录 引言一、Android Compose基本概念1.1 什么是Android Compose?1.2 Compose的优势1.3 如何在项目中使用Compose 二、Compose中的状态管理2.1 状态管理的重要性2.2 Compose中的状态和数据流2.3 使用State和MutableState处理状态2.4 通过ViewModel进行状态管理 三、Compose中的列表和滚动
阅读更多...
实例：如何统计当前主机的连接状态和连接数

实例：如何统计当前主机的连接状态和连接数

统计当前主机的连接状态和连接数 在 Linux 中，可使用 ss 命令来查看主机的网络连接状态。以下是统计当前主机连接状态和连接主机数量的具体操作。 1. 统计当前主机的连接状态 使用 ss 命令结合 grep、cut、sort 和 uniq 命令来统计当前主机的 TCP 连接状态。 ss -nta | grep -v '^State' | cut -d " " -f 1 | sort |
阅读更多...
状态模式state

状态模式state

学习笔记，原文链接 https://refactoringguru.cn/design-patterns/state 在一个对象的内部状态变化时改变其行为， 使其看上去就像改变了自身所属的类一样。 在状态模式中，player.getState()获取的是player的当前状态，通常是一个实现了状态接口的对象。 onPlay()是状态模式中定义的一个方法，不同状态下（例如“正在播放”、“暂停
阅读更多...
【反射知识点详解】

【反射知识点详解】

Java中的反射（Reflection）是一个非常强大的机制，它允许程序在运行时检查或修改类的行为。这种能力主要通过java.lang.reflect包中的类和接口来实现。 通过反射，Java程序可以动态地创建对象、调用方法、访问字段，以及获取类的各种信息（如构造器、方法、字段等）。 反射的用途 反射主要用于以下几种情况： 动态创建对象：通过类的Class对象动态地创建其实例。访问类的字段
阅读更多...
qml states 状态

qml states 状态

states 状态 在QML中，states用于定义对象在不同状态下的属性变化。每个状态可以包含一组属性设置，当状态改变时，这些属性设置会被应用到对象上。 import QtQuick 2.15import QtQuick.Controls 2.15// 定义应用程序的主窗口ApplicationWindow {visible: true // 使窗口可见width: 640 /
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2