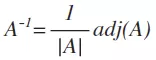伴随专题
线性代数 第二讲 矩阵_逆矩阵_伴随矩阵_分块矩阵_初等矩阵_矩阵的秩
矩阵 文章目录 矩阵1.矩阵的定义2.矩阵的运算法则3.特殊矩阵3.1 伴随矩阵3.2 可逆矩阵3.2.1 定义3.2.2 可逆矩阵的一些定理3.2.3 可逆矩阵公式与转置矩阵公式3.2.4 求逆矩阵 3.3 分块矩阵3.3.1 分块矩阵的运算3.3.2 分块矩阵的初等行变换(超纲内容但要了解) 3.4 初等矩阵3.5 行阶梯矩阵和行最简矩阵3.6 等价标准型与等价矩阵 4.矩阵的秩5.矩
求臻医学携伴随诊断试剂盒亮相第十三届病理年会
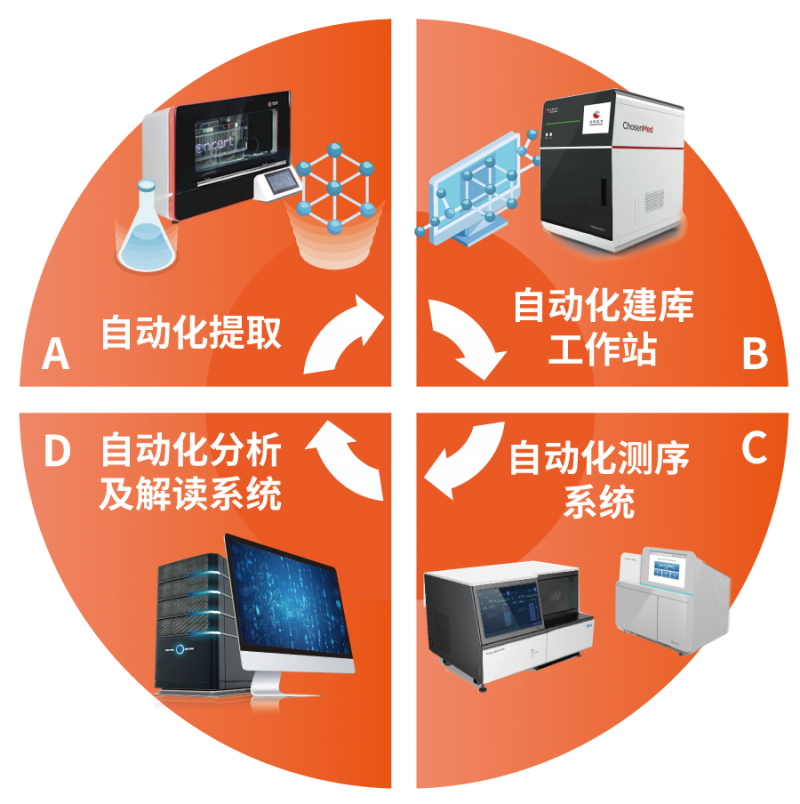
中华医学会病理学分会第二十九次学术会议暨第十三届病理年会于2024年3月28~31日在北京国家会议中心隆重召开。本次大会由中华医学会、中华医学会病理学分会主办,汇聚近万名病理学领域海内外知名专家,共同见证、推进中国病理学的传承、创新、发展。求臻医学作为肿瘤精准诊疗领域的佼佼者,携ChosenHawkEye®肺癌6基因突变检测试剂盒崭新亮相并分享专题讲座,共享其在肿瘤精准诊疗领域的最新研究成
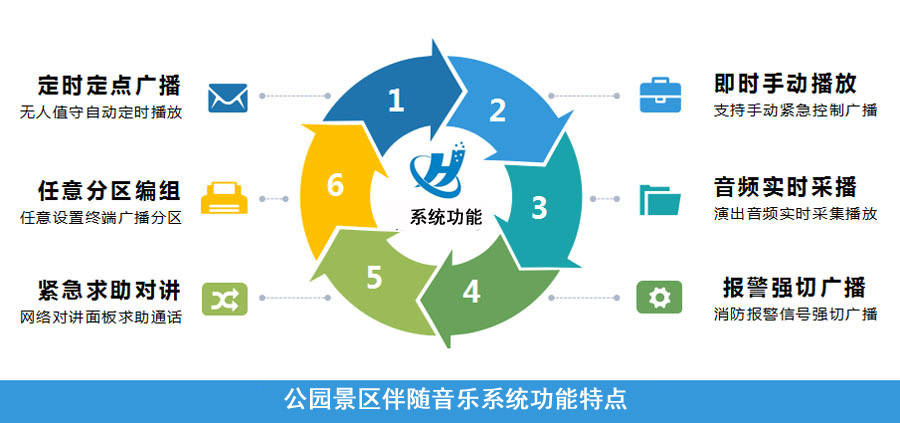
公园景区伴随音乐系统-公园景区数字IP广播伴随音乐系统建设指南
公园景区伴随音乐系统-公园景区数字IP广播伴随音乐系统建设指南 由北京海特伟业任洪卓发布于2024年4月23日 随着“互联网+”被提升为国家战略,传统行业与互联网的深度融合正在如火如荼地展开。在这一大背景下,海特伟业紧跟时代步伐,凭借其深厚的行业洞察力和前瞻性的技术视野,将广播系统与媒体交互技术、TCP/IP协议等先进科技相结合,为公园旅游景区带来了一款既具有前瞻性、又兼具应用性和科学
Pytorch:一维卷积及其伴随的定义
文章目录 一、数学表达二、步长2.1、步长的作用2.2、步长的示例步长为 1步长为 2 2.3、总结 三、零填充3.1、零填充的作用:3.2、类型和大小3.3、 应用示例 四、通道数4.1、通道数的定义4.2、示例说明4.3、深度学习中的应用 五、batch_size5.1、batch_size和数据形状5.2、举例解释 六、nn.Conv1d函数6.1、功能和使用6.2、参数详解6.3、p
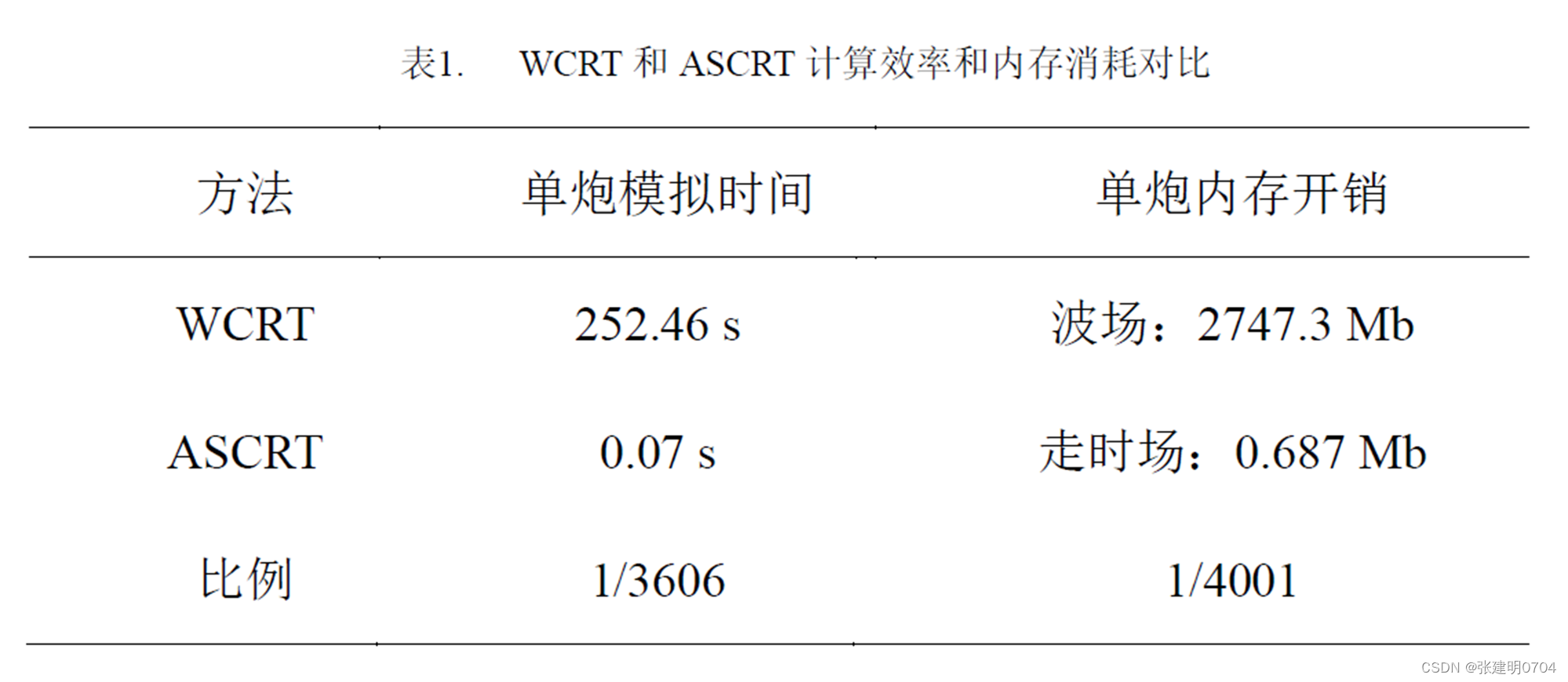
程函方程伴随状态法走时层析,初至及反射
该方法最初由Sei和Symes在1994年提出,Leung and Qian (2006)的文章有较细致的阐述,Taillandier(2009)又将该方法整理发表到地球物理权威期刊Geophysics上。国内由本人所在的课题组的谢春,刘玉柱,董良国教授等人在2014年引入,2017年李勇德、刘玉柱和董良国教授等人提出了预条件伴随状态法走时层析方法发表在地球物理学报上(该预条件方法后来由Hu等人(
线性代数笔记21——伴随矩阵和克莱姆法则
伴随矩阵 对于2×2矩阵来说,它的逆矩阵公式: 对于更高阶矩阵,我们也希望使用类似的公式。从2×2的逆矩阵公式可以看出,它的逆矩阵由两部分组成,其一是行列式的倒数,这意味着矩阵可逆的前提是行列式不为0,问题是另一部分是什么? 仔细观察,发现它和代数余子式有一定的关系,对于A来说: a的代数余子式: b的代数余子式: c的代数余子式: d的代数余子式:
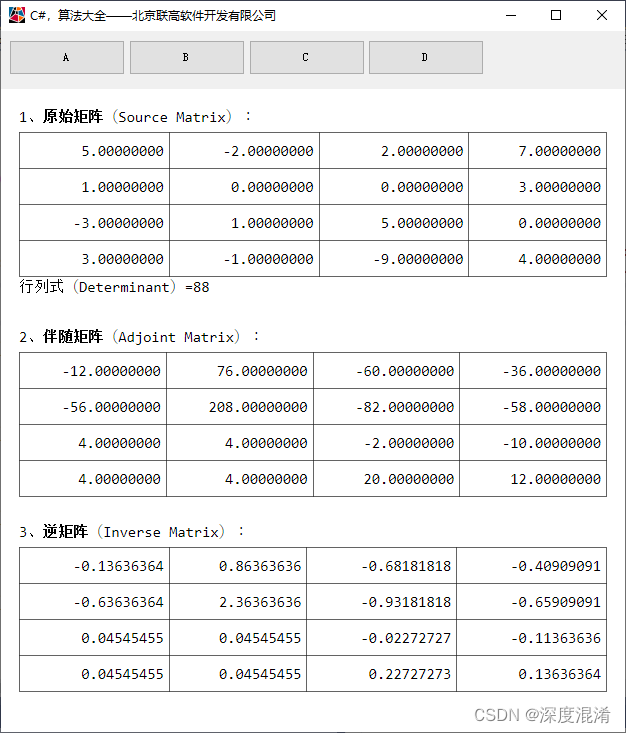
C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant) 矩阵行列式是指矩阵的全部元素构成的行列式,设A=(a)是数域P上的一个n阶矩阵,则所有A=(a)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。若A,B是数域P上的两个n阶矩阵,k是P中的任一个数,则|AB|=|A||B|,|kA|=kⁿ|A|,|A*|=|A|,其中A*是A
《线性代数:矩阵》:伴随矩阵
一、定义 矩阵 A 的行列式 |A| 所有的代数余子式所构成的形如 的矩阵称为矩阵 A 的伴随矩阵,记为 二、性质 对任意 n 阶方阵 A,都有伴随矩阵。
伴随开发人员成长的问题:工程重要,还是算法重要?细节重要,还是架构重要?
2005年12月04日 22:07:00 为了考虑一段代码中的字符串处理效率问题,我写了一个测试程序来检测字符串引用,然后把它贴在delphibbs里(http://www.delphibbs.com/delphibbs/dispq.asp?lid=1220572)。随后这引起了对软件工程和开发技巧的争论。下面的文字很大程度上代表了我当时(2002年中)对开发技术、技巧的观点,我想这与现在
构建人工智能系统并非一项简单的工作,每一个阶段都伴随着挑战
大多数企业都在增加人工智能方面的投资,因为疫情爆发。一些组织正在加速采用人工智能,以确保他们的业务不受当前疫情的影响。 但组织也需要认识到采用人工智能的挑战。构建人工智能系统并非一项简单的工作,每一个阶段都伴随着挑战。 即便你建立了一个人工智能项目,在部署时也会有很高的失败率,这可以归结为很多原因。本文将介绍人工智能项目失败的五个主要原因,并提到了成功实施人工智能项目的解决方案。
ATFX汇市:伴随美指进入弱势周期,USDJPY正向下试探140关口
ATFX汇市:12月美联储利率决议宣布暂停加息,鲍威尔表示“降息已开始进入视野”,市场人士对于降息的预期持续升温,美元指数从10月份开始进入弱势周期,至本周时,最低点已经突破102重要关口。受美指弱势周期影响,USDJPY启动中期下跌走势。11月14日至今,USDJPY累计跌幅-6.5%,最低触及140.9635点,如果跌势延续,未来数个交易日即可跌破140关口。日本央行虽然没有结束负利率政策,但
伴随高性能多级网关和多级分布式缓存架构应用实战经验
随着互联网业务的快速发展,对于高性能网络架构的需求越来越迫切。在这篇文章中,我们将介绍高性能多级网关和多级分布式缓存架构在实际应用中的经验,并提供相关示例代码。 一、高性能多级网关的设计与实现 高性能多级网关是一个重要的网络架构模式,通过将请求在多个层级进行处理,以实现高并发、低延迟的服务。以下是一个简单的高性能多级网关的设计和实现示例代码: // 处理请求的Controllerclas
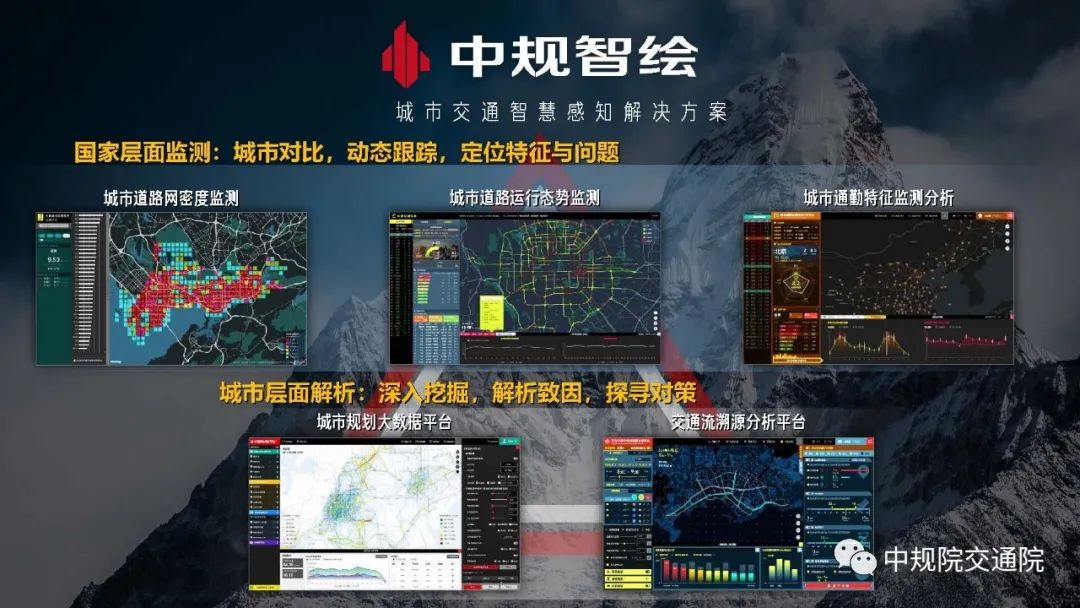
赵一新:数字伴随——城市交通的智慧感知
来源:中规院交通院 本文改编自中国城市规划设计研究院交通分院赵一新院长,在2020中国城市规划学术季“伴随•成长”主题活动中的主题演讲:《“数字伴随”——城市交通的智慧感知》。 赵一新 中国城市规划设计研究院城市交通研究分院 院长 “城市历史学家斯皮罗·科斯托弗把城市称作为一个“过程”,城市随着居住人群与科学技术演变而变化。人类用几千年的时间建造城市,可能需要用同样的时间来认识城市规律。”
Layui框架伴随图片上传需求的表单提交问题
表单提交难免会携带图片上传或附件上传等情况。 最近在使用Layui框架,Layui默认的form表单提交会自动监听其内的<button>标签,当点击button时自动触发表单提交事件。 同样,Layui的upload上传控件默认自动提交,也可以通过绑定另一个按钮,控制提交。 控件功能不再详述。 综上,最初的想法是,将upload通过绑定form的button,这样,点击form表单时,先触
伴随第四次电气革命实现半导体行业的可持续智能增长
本篇是关于施耐德电气SmartMCC和EOCR的故事 众所周知,半导体是韩国最具代表性的出口产品。尤其是机械化、自动化进入第四次工业革命时代,半导体可以说是所有机器的中心。 此外,随着物联网系统的建立和PC使用量的增加,半导体行业进一步壮大,开发全新、安全的解决方案非常重要。 换句话说,制造可持续和高效的半导体行业是关键所在。 第四次电气革命与半导体行业的相关性 值得注意的是,半
宫崎骏的动漫——伴随我成长的最美的片段
很多事情不能自己掌控,即使再孤单再寂寞,仍要继续走下去,不许停也不能回头。——《千与千寻》坚强,不是面对悲伤不流一滴泪,而是擦干眼泪后微笑着面对以后的生活。——《风之谷》有些心事只能自言自语,有些秘密只能讲给朋友。有些痛苦只能默默承受,自己还是要靠自己拯救。真正的痛苦,没有人能与你分担,你只能把它从一个肩头,换到你的另一个肩头。——《魔女宅急便》 到不了的地方都叫做远方,回不去的世界都叫做家乡,
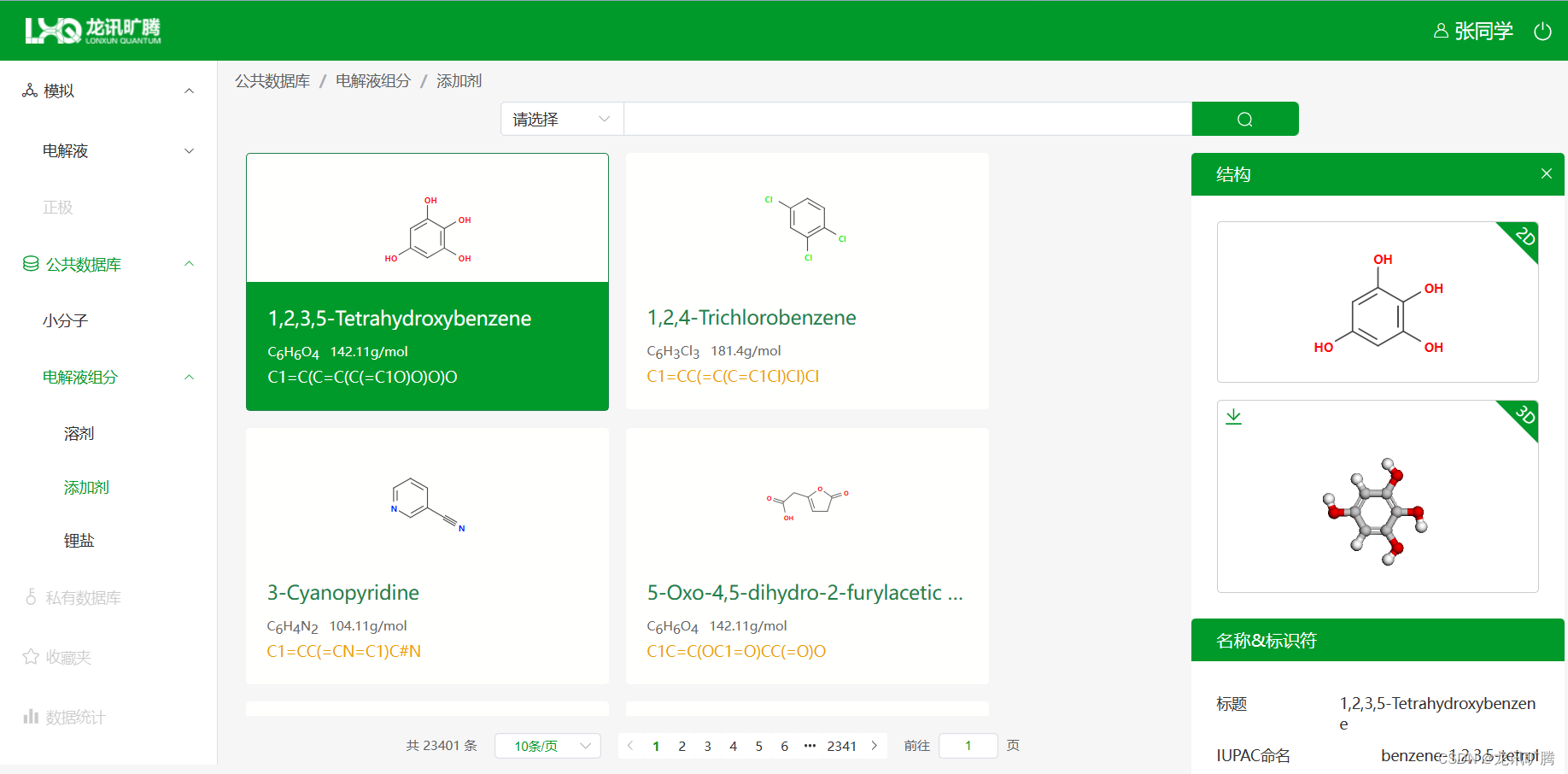
龙讯旷腾:如何建立基于第一性原理的正向研发模式,原子级计算伴随的时间和空间尺度增长将带来的变革
2023年10月8-11日,由中国材料研究学会主办的第四届中国新材料产业发展大会在浙江温州隆重举行。来自全国各地的6000余名新材料专家、企业家、投资家、当地高等院校和企事业单位的代表以及51位两院院士出席了本次大会。龙讯旷腾总经理吕海峰特邀做“先进材料数字化研发论坛”分论坛主持人并发表《人工智能驱动的超大规模微观材料计算方法及应用》主旨演讲。将围绕合金材料、新能源、半导体等新兴行业的发展,探讨如
龙讯旷腾:如何建立基于第一性原理的正向研发模式,原子级计算伴随的时间和空间尺度增长将带来的变革
2023年10月8-11日,由中国材料研究学会主办的第四届中国新材料产业发展大会在浙江温州隆重举行。来自全国各地的6000余名新材料专家、企业家、投资家、当地高等院校和企事业单位的代表以及51位两院院士出席了本次大会。龙讯旷腾总经理吕海峰特邀做“先进材料数字化研发论坛”分论坛主持人并发表《人工智能驱动的超大规模微观材料计算方法及应用》主旨演讲。将围绕合金材料、新能源、半导体等新兴行业的发展,探讨如
机器人中的数值优化(二十一)—— 伴随灵敏度分析、线性方程组求解器的分类和特点、优化软件
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例 三十三、伴随灵敏度分析 伴随灵敏度分析可以避免冗余信息的计算,在下面的例子中,我们