【视频异常检测】Diversity-Measurable Anomaly Detection 论文阅读

本文主要是介绍【视频异常检测】Diversity-Measurable Anomaly Detection 论文阅读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章信息：

发表于：CVPR 2023
原文链接：https://arxiv.org/abs/2303.05047
源码：https://github.com/FlappyPeggy/DMAD

Abstract

基于重建的异常检测模型通过抑制对异常的泛化能力来实现其目的。然而，多样化的正常模式因此也不能被很好地重建。虽然一些努力已经被做出来通过建模样本多样性来缓解这个问题，但由于不希望的异常信息的传递而导致了捷径学习。在本文中，为了更好地处理这个权衡问题，我们提出了多样性可测量异常检测（DMAD）框架，以增强重建多样性，同时避免对异常的不良泛化。为此，我们设计了金字塔变形模块（PDM），它从重建的参考到原始输入中估计多尺度变形场，以建模不同的正常模式并测量异常的严重程度。结合信息压缩模块，PDM本质上将变形与原型嵌入分离开来，并使最终的异常分数更可靠。对监控视频和工业图像的实验结果证明了我们方法的有效性。此外，DMAD在面对受污染的数据和类似异常的正常样本时同样有效。

1. Introduction

视觉异常检测是计算机视觉领域中的一个基本且重要的问题，广泛应用于视频监控和工业检测等领域。它旨在从已知类别中检测异常值和从未见过的类别中发现新的模式。这项任务非常具有挑战性，因为异常数据的分布多样且收集成本高昂。因此，我们必须在无监督设置下基于仅有的正常样本构建模型，以便高度区分正常和异常样本。

在过去的十年中，基于重构的方法在异常检测方面取得了巨大进展。这些方法使用自动编码器（AEs）或生成对抗网络（GANs）来从任何输入图像或视频帧中重新构建正常对应物。基于AE的方法首先将输入压缩以丢弃超出正常原型的信息，然后解码嵌入以重新构建输入。根据估计的重构误差，可以检测出异常。

然而，基于重构的方法在异常检测方面的性能长期受到一个严峻问题的限制，即在重构多样化正常和检测未知异常之间的权衡。为了更容易区分异常，先前的工作施加了更多的约束来抑制自动编码期间的异常信息，这导致对多样化正常实例的高重构误差。例如，在图1和图2g中，严重变形的正常（也称为异常样本）“7”的样本甚至比异常样本“4”的误差更高。为了更好地重构多样化的正常，每个查询向量对应于内存中的多个原型，即使异常投影远离原型，也可能被组合到异常嵌入中。因此，在原型嵌入之间的低可能性区域分布的异常很难从多样化正常中识别出来。MNAD引入了跳跃连接以进行多样化重构，并添加了额外的约束以解决错误组合问题。但是后者通过跳跃连接强制模型传输更多不受约束的异常部分信息，导致了捷径学习和不受欢迎的异常重构。

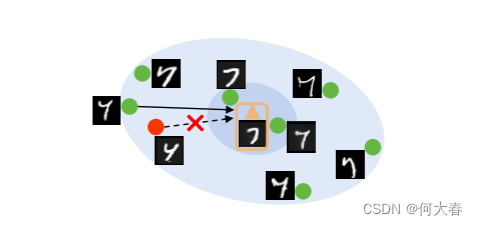
图1. MNIST数据集中异常检测困难的示例。原型由橙色三角形表示，异常由红色点表示。在这种情况下，基于重构误差或高维特征空间中的距离几乎无法检测到异常。我们的解决方案在图2中进行了说明。

解决上述权衡问题的关键是找到一个适当的多样性度量，该度量能够正相关地反映正常和异常样本的多样性，同时与异常的严重程度相关联。有了这样的度量，我们就不需要对抗正常重构的不完美或者不受欢迎的异常重构，因为异常可以通过多样性度量和重构误差一起更准确地检测出来。需要注意的是，像素级的重构误差不是多样性的理想度量，因为高误差区域经常会将多样化的正常与异常混淆在一起，例如，具有结构变形的正常与颜色接近背景的异常可能会产生不可靠的重构误差。

在本文中，我们提出了一种多样性可测量的异常检测（DMAD）框架，以增强重构多样性的可测量性，从而更准确地测量异常性。我们的基本思想是将重构分解为原型正常的紧凑表示和更多样化的正常与异常的可测量变形，从而将被低估的重构误差通过可以正确测量的多样性进行补偿。为此，DMAD框架包括一个金字塔变形模块（PDM）来建模和测量多样性，以及一个信息压缩模块（ICM）来学习原型正常模式。

受[4, 15]的启发，我们假设异常（例如在视频监控中）可以被表示为外观的显着变形，包括位置变化和微小运动。相比之下，各种各样的正常样本可以被表示为较弱的变形，因此可以很容易地与异常样本区分开来。因此，我们设计了PDM来建模正常样本的多样性以及异常的严重程度。具体来说，PDM学习了描述像素级转换方向和距离的分层二维变形场（图2c,d），从参考图（图2b，由内存中的原型重构而成）到原始输入。在ICM中，我们学习了作为稀疏原型的压缩表示。因此，单个内存项足以表示每个正常聚类。这比其他基于内存的方法更紧凑，其他方法通常需要多个内存项。通过将PDM与ICM集成，DMAD基本上将变形信息（图2e）与类原型分离开来，使最终的异常得分更具有区分性（图2f）。

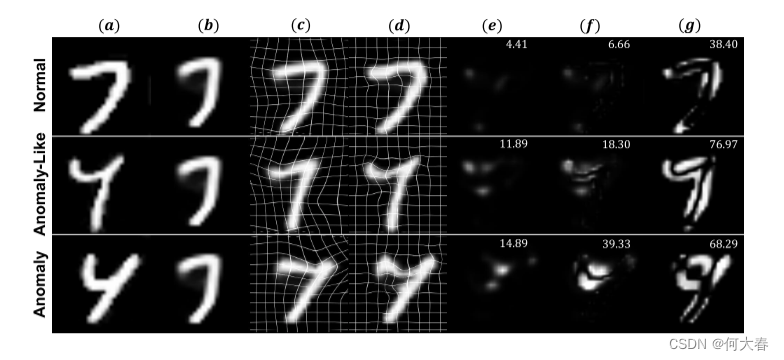
图2. 我们的多样性可测方法解决检测困难的示意图。白色数字表示异常分数。a) 原始输入; b) 重构的参考图像; c) 粗略变形; d) 细微变形; e) 多样性的度量; f) 添加了变形信息的误差图为类似异常的样本分配了比真实异常更低的异常分数; g) 像素级重构误差产生了不正确的异常分数。

我们在视频监控和工业缺陷检测的场景中评估我们的异常检测框架。为了在后一种情况下应用DMAD，我们提出了PDM的一种变体PPDM，以处理纹理重建中的误报问题。大量的实验结果验证了我们方法的有效性。此外，即使在受污染的数据和异常样法线面前，我们的方法也能很好地工作。我们工作的主要贡献如下：

• 我们引入了多样性可测量的异常检测框架，使基于重构的模型能够在重构各种各样的正常模式和检测未知异常之间实现更好的平衡。
• 我们提出了金字塔变形模块来实现多样性度量，其中变形信息明确地与紧凑的类别原型分离，由此产生的多样性度量与异常性呈正相关。
• 我们的方法在视频异常检测和工业缺陷检测方面优于先前的作品，并且在面对受污染数据和类似异常的正常样本时表现良好，展示了其广泛适用性和稳健性。

2. Related Work

Anomaly detection.基于重构的方法对正常数据的分布进行建模，并将重构误差较高的样本标记为异常，因为仅使用正常数据训练的模型无法重构异常数据。一些方法使用自动编码器来检测异常，例如卷积自动编码器[9]及其变种[24, 40]。其他方法引入额外的约束或记忆来使模型更具区分性。例如，稀疏编码[25, 39]通过正则化减少表示的冗余性；带记忆的自动编码器（MemAE）[8]使用外部记忆库记忆训练数据集中出现的正常模式；变分自动编码器[10, 35]假设正常数据的先验分布以约束非线性表示能力；HF2VAD [20]使用CVAE[33]捕获动态之间的相关性。帧预测[19]假设视频中的异常样本不能由不包含未见信息的过去帧表示，并迫使模型编码不同帧之间的变化。此外，自动编码器还可以与外部对象检测器[7, 14, 20]结合使用，以捕获与背景无关的外观。

尽管这些方法通常表现良好，但由于重构和区分之间的权衡问题，它们往往难以区分异常样本和类似异常的正常样本。在我们的框架中，利用金字塔变形模块和信息压缩模块来解决这一权衡问题，显著提高了异常检测性能。

Memory network.生成模型在特征空间中连续映射，可能会将异常赋予比正常样本更高的概率[28]。最近的研究[8,11,20,29]探索了使用离散外部存储器来生成已见的正常模式的应用，即使输入是异常的。MemAE [8]提出了一种记忆增强型自编码器，它使用编码器的信息作为查询，并从存储模块中获取检索到的正常模式。MNAD [29]引入了跳跃连接来缓解多样化的正常模式可能产生高重构误差的问题。HF2VAD [20]将存储模块扩展到多级存储，并使用额外的估算器[3,13]来明确建模运动信息并过滤背景中的噪声。DAAD [11]使用分块存储器来增加存储器的特异性。

在大多数现有的工作中，存储模块输出存储项的线性组合，这可能导致类似正常的异常不良重构。而它们并没有明确考虑到，对应于相同存储格的实例可能位于接受域的不同位置。在我们的方法中，通过将嵌入压缩为单个存储项来缓解这些问题，以确保输出绝对正常。

Transformation modeling.视频帧之间的转换是异常检测的关键线索。一些方法[7, 14, 19, 20]使用外部对象检测器或光流估计器隐式或显式地建模运动信息。在转换估计器中，光流估计[13]被广泛研究，旨在估计连续帧之间的像素级运动。此外，对成对图像之间的对应建模也应用于2D几何匹配[30]和3D图像配准[36]以获得图像变形场。STN [15]学习将原始图像自身进行转换，以提高识别算法的性能。RegAD [12]使用特征级仿射配准来重新定位特征而不改变嵌入。

然而，成对转换建模仅关注模式变化，因此无法检测静态异常。而预训练的转换估计器在不同场景中引入了泛化误差。相比之下，我们通过在端到端训练中将转换与原型内存分离和测量来解决这些问题。

3. Diversity-Measurable Anomaly Detection

在本节中，我们首先分析了基于重构的异常检测的目标，并提出了一个多样性可测量的框架，以解决现有工作中的权衡问题。然后，我们介绍了信息压缩模块和金字塔变形模块（PDM）作为该框架的实现。最后，我们解释了训练和推断过程，以及如何使用PDM的变体将该框架应用于缺陷检测。

3.1. The framework

给定输入$x$，基于自编码器的方法旨在通过最小化以下重构损失（其中$\Vert .{\Vert }_2$只是一种重构损失的类型）来建模正常数据分布：

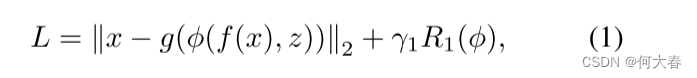
对于编码器$f(\cdot )$、解码器$g(\cdot )$、潜变量$z$（在这些情况下是指离散记忆项）以及对应于其约束$R_1(\varphi )$的受限特征映射函数$\varphi (\cdot )$，我们考虑最小化上述重构损失。为了生成多样化的正常模式，引入了跳跃连接和连接$[\cdot ,\cdot ]$[29]：

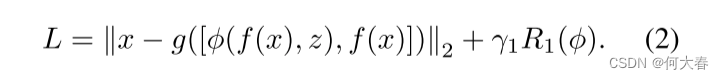
然而，由于数据分布的多样性，先前的方法不得不面对代表多样化正常情况和检测异常之间的冲突。其固有原因在于多样性编码[·, f(x)]包含无法准确测量的冗余信息。

在这项工作中，我们提出了一个基于原则的框架，称为多样性可测量异常检测（DMAD），以缓解这种冲突。基本思想是限制传输到 $g(\cdot )$ 的异常信息，同时测量和建模其余部分的多样性。为此，我们设计了信息压缩模块 $\varphi (\cdot )$ 和多样性感知模块 $\psi (\cdot )$，在 DMAD 框架下：

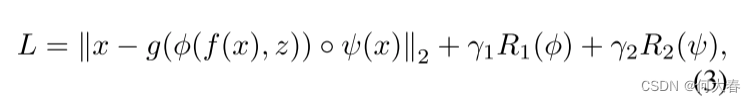
其中，$\circ$表示聚合运算符。通过适当设计 $\varphi (\cdot )$、$\psi (\cdot )$和约束条件，重建损失的优化可以提高特征嵌入的紧凑性。这样，多样化的表示通过$\varphi (\cdot )$映射到内存中的紧凑原型。输入 x 相对于其重建的多样性由 $\psi (\cdot )$表示。在 $\psi (\cdot )$中测量到的多样性可以弥补对重建误差的低估，这是产生准确异常分数的关键因素。

在满足以下条件（图3）的前提下，该框架可以实现我们的目标：1. $\psi (\cdot )$能够从原型模式到任何正常输入中学习所有的多样化信息，以确保正常样本不会产生高异常分数；2. $\psi (\cdot )$生成的变形与多样性度量呈正相关；3. 由 $\psi (\cdot )$表示的有关 $x$ 的原型信息需要最小化。在接下来的小节中，我们将解释如何设计模块来满足这些条件。

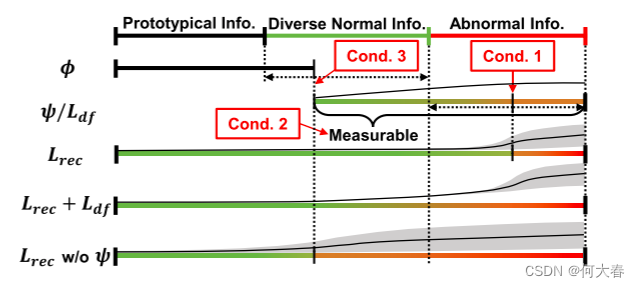
图3.DMAD 框架的三个条件。线条的颜色表示多样性（异常程度）的测量值；灰色区域表示测量的不确定性；双虚线箭头表示边界的可能范围。最后两行分别表示 DMAD 和传统的基于重构的方法。

3.2. Information compression module

根据 [35]，我们采用 VQ-Layer 作为信息压缩模块来学习 $\varphi (\cdot )$，给定嵌入 $f(x)\in R^{D\times H^{\prime }\times W^{\prime }}$ 作为查询 $z^e=f(x)$，并且记忆 $z\in R^{D\times N}$。然后，通过寻找具有最小 $L2$ 距离的记忆项（图 4 中的“搜索”），将 $z_e$ 量化为单个记忆特征立方体 $z_q\in R^{D\times H^{\prime }\times W^{\prime }}$。

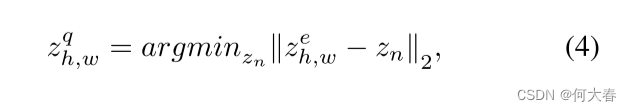
这里，$z_n$ 表示第 $n$ 个记忆项， h ∈ { 1 , ⋅ ⋅ ⋅ , H ′ } h ∈ \{1, · · · ,H'\} h∈{1,⋅⋅⋅,H′} ， w ∈ { 1 , ⋅ ⋅ ⋅ , W ′ } w ∈ \{1, · · · ,W'\} w∈{1,⋅⋅⋅,W′} 表示 $z_q$ 和 $z_e$ 中相同的位置。使用 stop-gradient 运算符 $SG(\cdot )$ 来更新其参数，压缩损失 $L_{com}$ 由超参数 $\beta$ 加权组合：

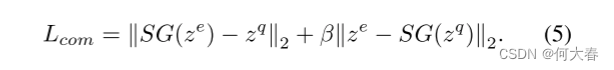
可以使用信息容量较低的跳跃连接（图 4 中的 “$Comp$.”）来进一步提高重建质量，而不会引入过多的泛化（即对中间特征使用带有 stop-gradient 运算符的 Conv-Layer，其缩减因子为 16 或更大）。

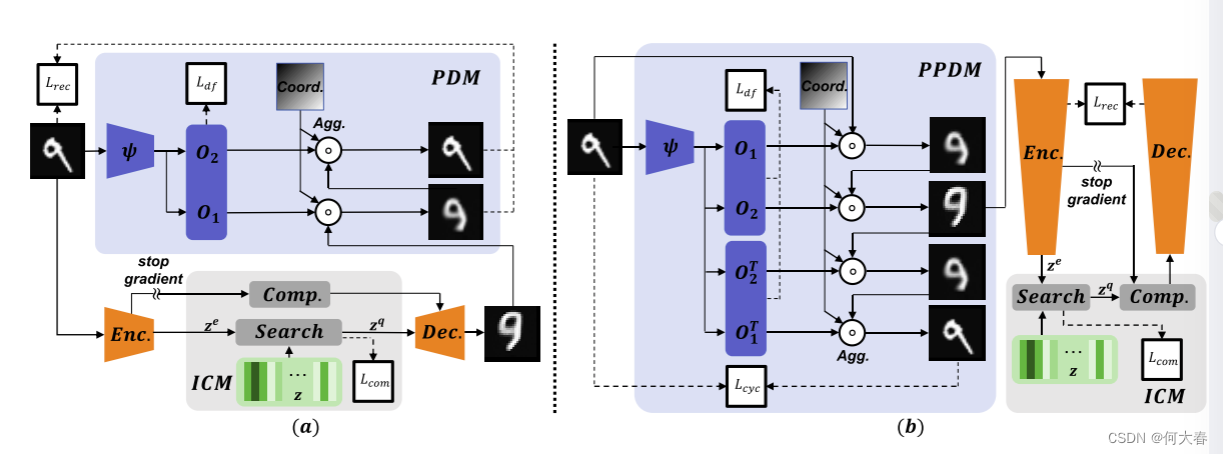
图 4. 多尺度金字塔形变场的两个版本多样性可测量异常检测框架。用 $\mathrm{O}$ 表示前向形变过程，反向过程为 ${\mathrm{O}}^T$。a) PDM 版本在重建后计算前向形变 $\mathrm{O}$。b) PPDM 版本采用循环一致的前向-反向形变，前向形变应用在输入上。

3.3. Pyramid deformation module

我们将未知的异常分为以下三种类型：未见类别（例如，新颖的对象）、全局异常（例如，意外的移动）和已见类别的局部异常（例如，奇怪的行为和工件损坏）。未见类别往往可以根据重建结果轻松检测，但后两种类型通常会与多样化的正常样本混淆。为了将这些异常与正常样本区分开来，我们使用可测量的形变来表示多样性，即重建参考图像与原始输入之间的形变，这样，正常样本中会出现轻微的形变，而异常样本中会出现剧烈的形变。

受到 STN 和 DCN [4,15] 的启发，我们引入了金字塔形变模块（PDM），该模块明确地学习具有分层尺度的形变场，以模拟不同异常类型的运动、行为和缺陷，如图 4a 所示。具体而言，在特征提取之后，$\psi (\cdot )$ 使用 $K$ 个头来计算偏移量 $\mathrm{O}$ = { O 1 , ⋅ ⋅ ⋅ , O K } \{O_1, · · · , O_K\} {O1​,⋅⋅⋅,OK​}，对应 $K$ 个粗到细的形变：

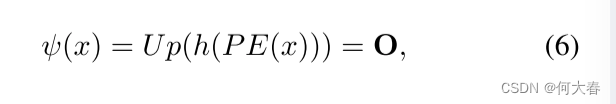
这里的 $PE(\cdot )$ 是位置嵌入算子 [18]，$h$ : R C × H × W → R 2 × { H 1 × W 1 , ⋅ ⋅ ⋅ , H K × W K } R^{C×H×W} → R^{2×\{H_1×W^1,··· ,H^K×W^K\}} RC×H×W→R2×{H1​×W1,⋅⋅⋅,HK×WK} 是形变估计器，生成偏移向量，$Up(\cdot )$ 是上采样函数，将 $K$ 个头的输出调整为与原始图像相同大小。在我们的实验中，我们设置 $K$ = 2，其中 $O_1$ 用于估计粗略形变（例如，对应于行人的位置或工件的摆放位置），而 $O_2$ 用于估计细微形变（例如，对应于行人行为或工件细节）。

考虑到没有位置信息的量化嵌入可能导致不准确的重构，我们还为解码器 $g(\cdot )$ 引入位置嵌入算子。然后，我们将$\mathrm{O}$ 聚合到重构的参考图 $g(PE(z^q))$ 上，得到由第 $k$ 层形变场校准的 ${\tilde{x}}_k(k=1,...,K)$。

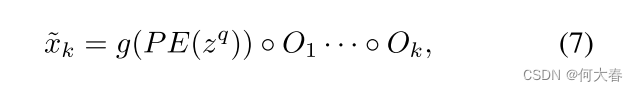
其中，$\circ$是在此实现中带有参考坐标的网格采样函数（图 4 中的“Agg.” 和 “Coord.”）。然而，针对 $\psi (x)$ 最小化无约束的重构损失可能会导致编码器 $f(\cdot )$ 的退化解。为了解决这个问题，我们通过梯度运算和强度损失添加了平滑度损失的约束，如下所示：

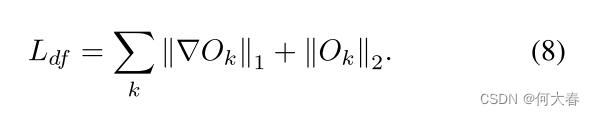
3.4. Foreground-background selection

将背景信息存储在存储器中将破坏嵌入的紧凑性并且需要大量的存储器项。此外，变形估计不应应用于背景。一些方法使用外部估计器来消除背景的干扰，但是在不同场景中的泛化不能得到保证，并且额外的噪声将不可避免地被引入。由于固定视角视频具有强大的先验知识，我们使用可学习的模板 $x_{bg}$ 来建模背景，并使用 $f_m(\cdot )$ 生成一个二进制掩码来指示像素是否属于前景或背景。第 $k$ 个头部的最终重构 ${\tilde{x}}_k$ 为：

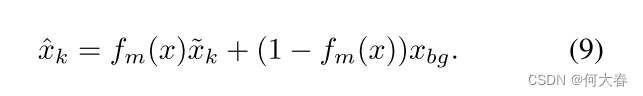
3.5. Training and inference

Training phase.一旦我们获得了重构 ${\tilde{x}}_k$，我们就可以计算重构损失 $L_{rec}$ 如下：

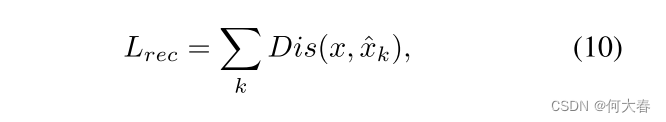
这里的 $Dis(\cdot )$ 是样本空间中的距离函数。回想一下方程 3 中的优化目标，我们使用 $L_{com}$ 和 $L_{df}$ 实现了两个约束。最后，训练通过最小化总损失来完成：

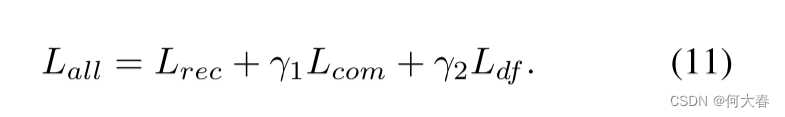
Inference phase.在推断阶段，我们使用 $\mathrm{O}$ 和重构损失来计算输入样本 $x$ 的误差图：

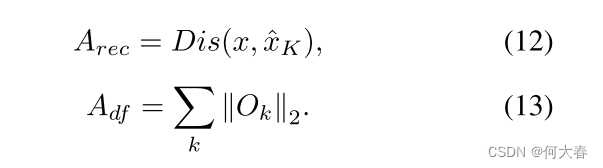
基于局部最大值计算图像级异常分数：

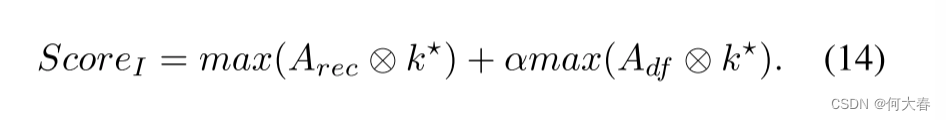
其中，$\otimes$ 表示卷积运算符，$k^{\star }$ 是用于异常图的卷积核。 $\alpha$ 是一个权衡参数。也就是说，重构损失和变形共同决定了异常分数，这比传统的基于重构的方法更有效，如图 3 所示。

4. Experiments and Analysis

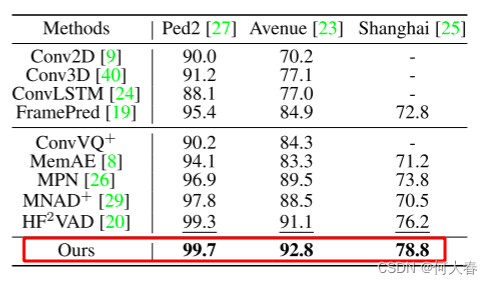
5. Conclusion

在本文中，我们提出了一种基于重建的多样性可测量异常检测框架，该框架同时增强了异常区分能力和重建多样性。为了实现这一目的，我们提出了金字塔变形模块与信息压缩模块一起使用。PDM显式地模拟了从参考到原始输入的多尺度变换场，而不依赖于外部估计器。因此，可以准确重建多样性正常模式并且可以准确测量异常的严重程度。对视频和图像基准数据的实证研究表明了我们工作的有效性和适用性。在未来的研究中，我们将进一步探索多样性感知模型用于异常检测。

注：
我并没有对图像一场检测那部分进行过多关注，有时间的话再研究工业一场检测那部分的。

更新：简单跑了一下代码，这两天看看代码看看

这篇关于【视频异常检测】Diversity-Measurable Anomaly Detection 论文阅读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---