本文主要是介绍[ABC216H]Random Robots,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Random Robots
题解
首先看到 k ⩽ 10 k\leqslant 10 k⩽10的数据范围限制,应该很容易联想到状压。
同时题目有时要求路径无交,很容易想到通过容斥来转移。
我们定义 d p S dp_{S} dpS为对于集合为 S S S的点的合法方法数,考虑怎么对其进行转移。
我们如何处理两点的路径是否有交,可以直接根据两点的终点进行判断。
我们可以从左到右枚举点作为终点,加入状态,我们 d p dp dp会按照终点的顺序将机械人加入状态。
当我们枚举点 p p p作为机械人 x x x的终点,如果有比机械人 x x x编号大的机械人已经加入状态,那么那个机械人一定与我们的机械人 x x x有交点。
但并非编号比他小的机械人终点在它后面就与它没有交点,可能会有这种情况:
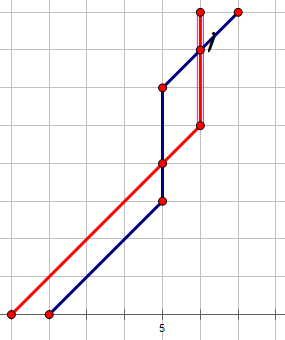
但这种情况我们可以将两者的终点交换一下,得到
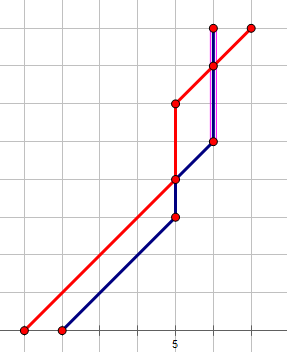
相当于我们同样可以用不合法的情况将其容斥掉。
不如说当我们先加入红色节点,再加入蓝色节点时会产生上面的情况,而下面的情况自身是不会加入到状态中的,只会有我们在先加入蓝色节点,再加入红色节点时将其减去,以除掉上面的不合法状态。
事实上,我们一个机械人会与许多机械人产生交点,所以我们同样需要通过容斥来维护我们的 d p dp dp答案,一面重复减去同一方案。
如果一个机械人与奇数个机械人在终点上产生逆序对,我们就要减去该方案,与偶数个机械人产生逆序对就加上该方案。
而一个机械人从起点 a i a_{i} ai走到终点 b i b_{i} bi会走 b i − a i b_{i}-a_{i} bi−a
这篇关于[ABC216H]Random Robots的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




