GDPU 算法分析与设计天码行空2

本文主要是介绍GDPU 算法分析与设计天码行空2，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、【实验目的】

（1）理解分治策略的设计思想；
（2）熟悉将伪码转换为可运行的程序的方法；
（3）能够根据算法的要求设计具体的实例。

二、【实验内容】

有n片芯片，其中好芯片比坏芯片至少多1片，现需要通过测试从中找出1片好芯片。测试方法是:将2片芯片放到测试台上，2片芯片互相测试并报告测试结果:“好”或者“坏”。假设好芯片的报告是正确的，坏芯片的报告是不可靠的。请设计一个算法，使用最少的测试次数来找出1片好芯片。

提示:可参考教材P29页的算法2.3. 测试函数可以采用以下方法。
在这里插入图片描述

三、实验源代码

#include<bits/stdc++.h>using namespace std;
const int n = 17;
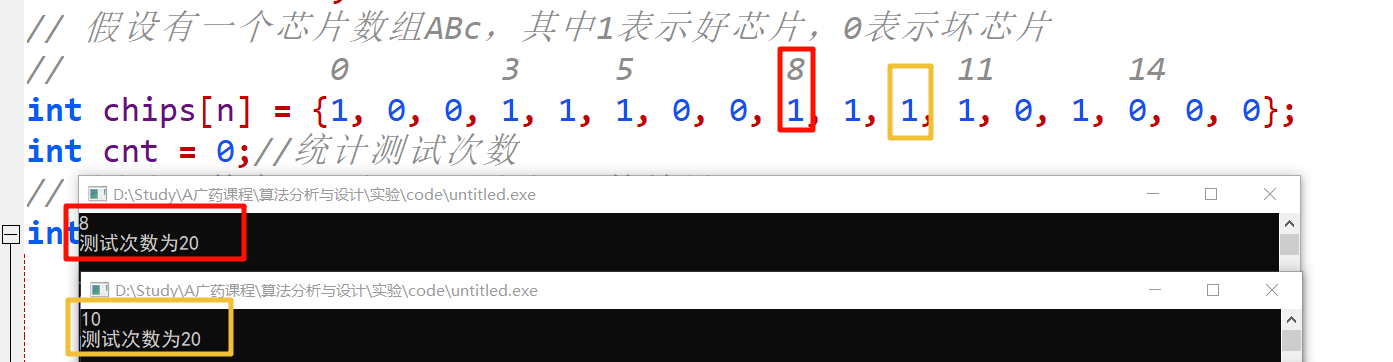
// 假设有一个芯片数组ABc，其中1表示好芯片，0表示坏芯片
//				0        3     5        8        11       14 				
int chips[n] = {1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0};
int cnt = 0;//统计测试次数
// 测试函数实现,返回 a 测试 b 的结果
int X_test(int a, int b) {cnt++;if(chips[a]==1)//好芯片返回正确的值return chips[b];return rand()%2; //坏芯片返回随机值
}int main() {// 初始化随机数种子srand(time(NULL));queue<int> remain;//队列存储剩余的芯片的下标for(int i = 0; i < n; i++)remain.push(i);int m = n;while(m > 3){for(int i = 0;i < m/2; i++)//每次比对 m/2 组,两个一组{int idx1 = remain.front();remain.pop();int idx2 = remain.front();remain.pop();
//			cout << "移除: " << idx1 << " " << idx2 << endl;int a = X_test(idx2,idx1);// 2 对 1 的测试结果int b = X_test(idx1,idx2);// 1 对 2 的测试结果if(a == b && a == 1)// a好 b好：留一个{
//				cout << "===添加: " << idx1 <<endl;remain.push(idx1);//假设留 idx1（留哪个都行）}if(remain.size() <= 3)break;
//			否则，两个都丢，上边已经pop掉了}m = remain.size();//更新剩余的分组数}if(remain.size() == 3){	int idx1 = remain.front();remain.pop();int idx2 = remain.front();remain.pop();int idx3 = remain.front();
//		cout << "最后移除" << idx1 << " " << idx2 << endl;//只要有一个测试结果是坏的情况，那没测试的 idx3 就是好的if(!X_test(idx1,idx2) || !X_test(idx2,idx1)){cout << idx3 << endl;cout << "测试次数为" << cnt << endl;exit(0);}
//		走到这里只有 两个测试结果都是好的情况cout << idx1 << endl;//随机输出一个即可cout << "测试次数为" << cnt << endl;exit(0);}
//	remain.pop();cout << remain.front() << endl;cout << "测试次数为" << cnt << endl;return 0;
}