【论文笔记合集】ARIMA 非平稳过程通过差分转化为平稳过程

本文主要是介绍【论文笔记合集】ARIMA 非平稳过程通过差分转化为平稳过程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

本文作者： slience_me

文章目录

ARIMA 非平稳过程通过差分转化为平稳过程
- 文章原文
- 具体解释
- 详解参照

ARIMA 非平稳过程通过差分转化为平稳过程

文章原文

Many time series forecasting methods start from the classic tools [38, 10]. ARIMA [7, 6] tackles the
forecasting problem by transforming the non-stationary process to stationary through differencing.
许多时间序列预测方法都是从经典工具开始的[38，10]。ARIMA [7，6]通过差分将非平稳过程转换为平稳过程来解决预测问题。

这句话提到了许多时间序列预测方法通常从经典工具开始，并提到了其中的一个经典工具是ARIMA模型。

ARIMA（自回归综合移动平均模型）是一种经典的时间序列预测方法，它通过将非平稳过程通过差分转化为平稳过程来解决预测问题。在时间序列分析中，许多时间序列数据都具有非平稳性，即它们的统计特性（如均值和方差）随着时间而变化。ARIMA模型通过对时间序列进行差分操作，将原始序列转换为一个平稳的序列，然后在这个平稳序列上建立自回归和移动平均模型，以进行预测。

因此，这句话指出了ARIMA作为一个经典工具，它通过将非平稳的时间序列转换为平稳的时间序列，然后利用这个转换后的序列来建立模型进行预测。

具体解释

让我们以一个简单的例子来解释非平稳过程如何通过差分转化为平稳过程。

假设我们有一个包含每月销售额的时间序列数据，而且我们发现这个时间序列在长期趋势上呈现增长或下降的情况，即它是一个非平稳序列。我们想要预测未来的销售额，但由于数据的非平稳性，我们不能直接应用许多经典的时间序列预测方法。

为了将这个非平稳过程转化为平稳过程，我们可以对时间序列进行差分操作。差分操作是指将当前时刻的值减去前一个时刻的值，得到一个新的序列。这个新的序列通常称为一阶差分序列。

例如，假设我们有以下月销售额的时间序列数据：

月份    销售额
1       1000
2       1100
3       1200
4       1300
5       1400

我们可以对销售额序列进行一阶差分操作：

月份    一阶差分销售额
2       1100 - 1000 = 100
3       1200 - 1100 = 100
4       1300 - 1200 = 100
5       1400 - 1300 = 100

现在我们得到了一阶差分序列，这个序列看起来是平稳的，因为它没有明显的趋势或周期性。接下来，我们可以在这个差分序列上应用ARIMA等经典方法来建立模型和进行预测。通过这种方式，我们成功地将原始的非平稳过程转化为一个平稳过程，使得我们可以更准确地进行预测。

借用知乎随风的图记录一下

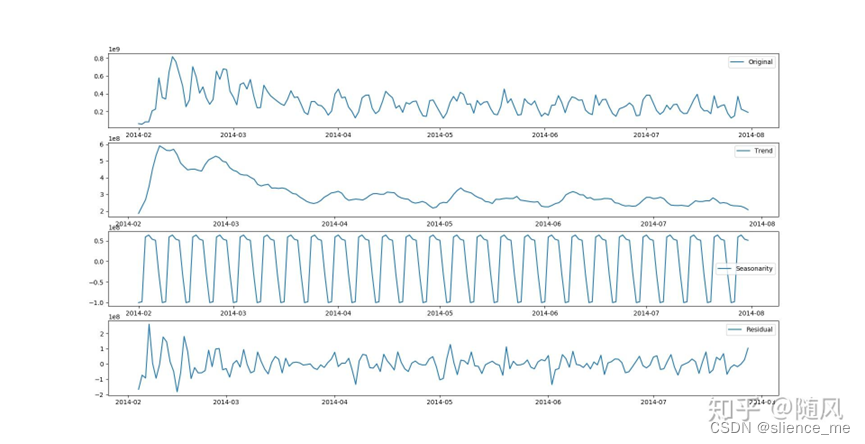
在这里插入图片描述
四个序列从上到下依次表示：原始序列、趋势序列、季节序列、残差序列。

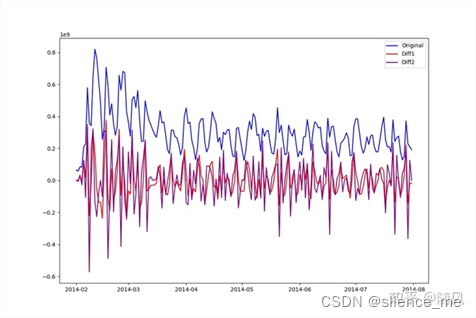
从上图中可以看出，经过一阶差分，原序列的趋势（有趋势一定是非平稳的）被消除了，整个序列基本围绕确定的均值震荡。经过二阶差分，与一阶差分相比，只是在震荡幅度上扩大了，因此对于该序列，采用一阶差分比较合适。一般情况下，采用一阶、二阶差分就可以使序列变得平稳。