本文主要是介绍深度学习入门课程学习笔记02 得分函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本篇学习笔记对应深度学习入门课程 第三课 得分函数
前向传播之-得分函数
剧透:深度学习必备的两个大知识点分别是前向传播和反向传播啦,这里节课我们会先着手把前方传播的所涉及的所有知识点搞定!我相信这部分对于咱们即便没有什么基础的同学来说也是很容易理解的。
得分函数:这个就是咱们这节课最核心的一个问题啦。什么叫得分函数呢?下面这个图就给了我们一个最直接的答案!
得分函数的目的:我们要做的就是对于一个给定的输入,比如一张小猫的图片,通过一系列复杂的变换(中间的过程咱们暂且当做一个黑盒子)能得到这个输入对应于每个类别的得分数值。
可能有些同学对于一个输入的图片如何计算出它的得分还有点困惑,这里我简单的来说一下从输入到输出的一个矩阵计算过程。
矩阵求解过程理解:首先对于一个32*32*3的输入,我们把它拉伸成一个列向量,也就是一个3072*1的向量,咱们下面用最简单的线性分类来解释整个过程,在线性分类中,我们需要权重参数W和B,那么W是整个线性分类的核心参数,我们要把一个输入分成10个类别并且对于每个类别给定一个得分数值,这样咱们的W参数矩阵就是一个10*3072的矩阵,我们可以通俗的理解成对于每一个类别我们都有3072个小参数去和咱们的输入(3072维的列向量)去计算最终的的分值,那么10就是我们最终要输入多少个类别。参数B就很好理解啦,这里咱们就不说啦。
得分函数计算实例:上图就是一个得分函数计算的最简单的一个流程,我们假设图像是有4个像素点组成的,然后咱们把它拉成了一个列向量(Xi),权重参数W是一个3*4的矩阵,因为咱们要把输入分成三个类别,最终再加上参数b得到了最终这只小猫属于每个类别的得分数值。
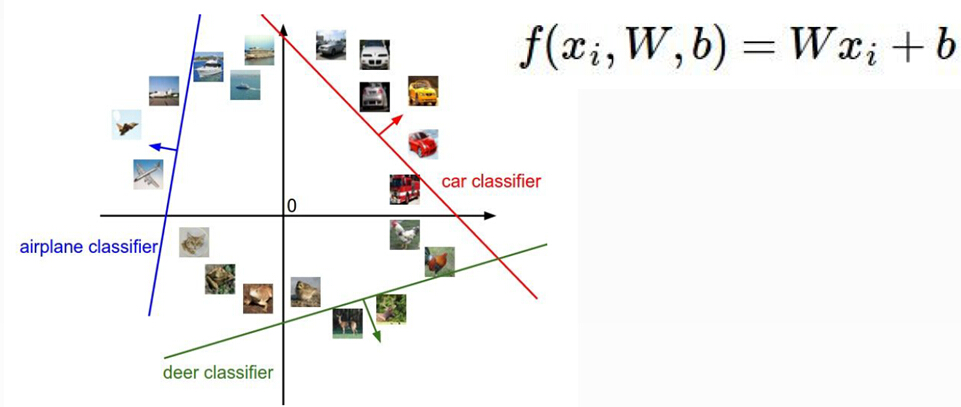
理解参数W和b:下面咱们再通过这张图来形象的理解下参数W和b,在真实的情况下对于每一个类别的参数W是一个3072维的,但是咱们为了形象化理解把它画在了2维的空间中,我们可以从图中看到三种颜色的线代表了三个线性分类器,参数W的每一个小权重的改变(共有3072个小权重)意味着这条线在改变的小参数的那个维度发生了偏转,我们可以想象2维空间中对于W的改变意味着什么然后再去想象这个3072维的空间。那么这个b参数是不是就没用呢?(有用你干嘛一直不说?)其实参数b是比不可少的,因为如果没有b那么所有的分类线都会交集与零点,这显然是不可取的嘛。
小总结:咱们这节课很轻松吧,但是如何从一个输入计算出它最终属于每一个类别的得分在一个实际的深度学习网络中可没这么简单就搞定,我这样做只是让大家能更好的理解这个得分函数。
笔记对应课程:深度学习入门课程 第三课
这篇关于深度学习入门课程学习笔记02 得分函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!