应用SPSS探索性分析，快速检查数据异常值

IBM SPSS Statistics探索性分析是描述统计中的一种分析方法，提供了数据过滤、离群值识别、假设检验等分析功能。

探索性分析中比较常用的功能是，通过数据过滤的功能，如分析数据中的极值、平均值、方差等，识别数据中的异常值；或使用检验的方法，判断后续使用的统计分析方法是否合适等，比如数据的正态分布假设是否成立。

一、示例数据

本文中，我们将会分析一组包含性别、客单价的数据。

通过探索性分析，查看数据中是否存在一些异常值，以及检验不同性别的客单价数据是否符合正态分布。

为什么要检验数据是否正态分布？这是因为在一些相关性分析（或其他分析）中，是以数据正态分布为前提进行统计分析的，如果数据不满足正态分布的假设，分析得出的结果就会不准确。

图1：示例数据

二、应用探索性分析

如图2所示，我们先打开IBM SPSS Statistics的探索分析选项（分析-描述统计-探索），然后再逐步演示操作。

图2：探索性分析

1、选择变量

如图3所示，探索分析设置面板中的选项含义如下：

1. 因变量列表，即随自变量变化的数值，本例中选取客单价作为因变量

2. 因子列表，用于定义个案组，可选择一个或多个因子变量，本例中选取性别

3. 个案标注依据，用于标记个案，本例中选取账号

通过以上的设置，我们将会获取到不同性别客单价的探索性分析结果。

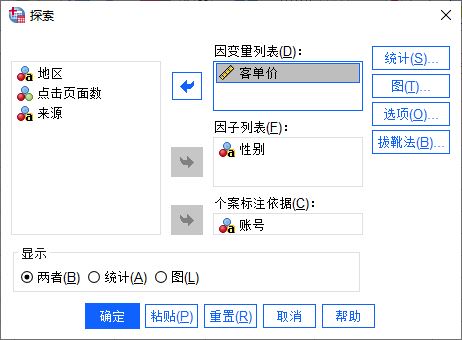
图3：频率分析中的图表功能

2、应用统计分析

完成变量的选择后，单击右侧的统计，开启如图4所示的统计面板，其中的数值应用如下：

1. 描述，提供了平均值、中位数、方差、最大值、偏度等统计数值，可设置平均值的置信区间

2. M-估计量，为每个个案的数值应用权重，有助于减少极端值、异常值对平均值和中位数的影响

3. 离群值，即极值的分析，包含最大值、最小值

4. 百分位数，可将排序后的数据进行指定百分位值分组

本例中，我们选取了描述、M-估计值与离群值的数值。

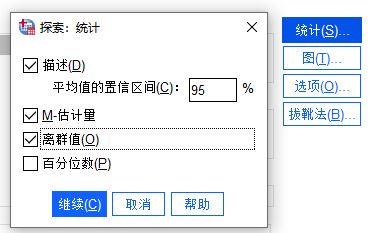
图4：探索性统计分析选项

3、解读统计分析结果

从分析结果来看，如图5所示，当前数据包含了50个男性客单价个案，以及49个女性客单价个案。

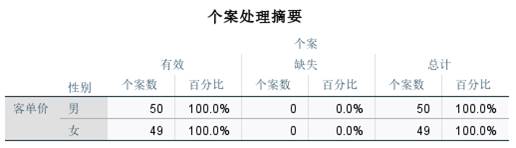
图5：频数统计

如图6所示，从描述数据可以看到，男性的客单价平均值为100.8，而女性客单价平均值仅为47.6

而男性客单价平均值的95%置信区间上限中，平均值达到188，说明存在一些极端值，进一步查看最大值数据，发现最大值达到2000。

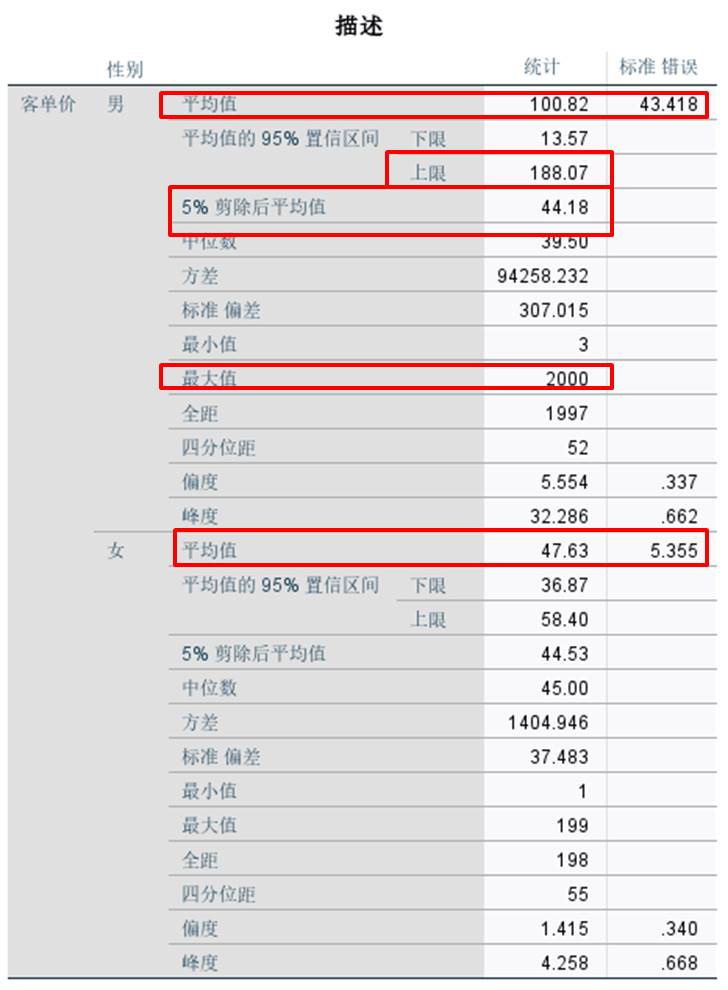
图6：描述性数值

这个最大值2000是单个个案，还是多个个案呢？另外，除了最大值外，是否存在其他极端值。为了解答以上问题，我们可以进一步查看极值分析。

如图7所示，可以看到，男性客单价中，账号77与账号85的客单价都属于极端值。

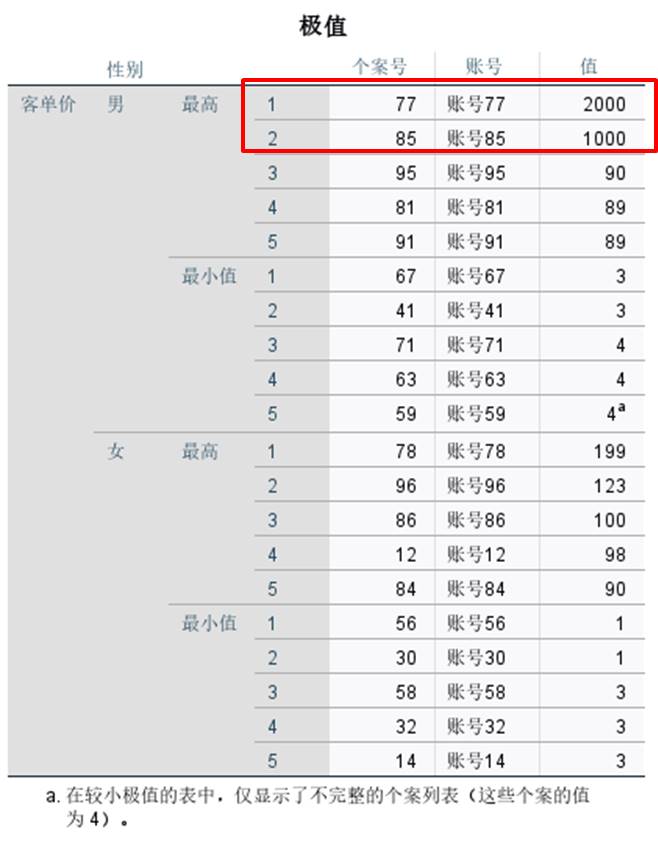
图7：极值分析

为了避免这些极值的影响，我们可以查看M估计量。如图8所示，经过M估计量的加权后，男性客单价平均值就变得比较正常了。

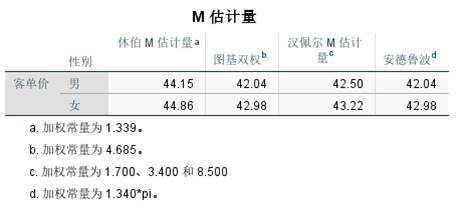
图8：M估计值

综上所示，通过IBM SPSS Statistics探索性分析的描述性统计数值，可获取到数据的平均值、极值等统计数值，有助于检查数据中的异常值情况。

另外，在《应用SPSS探索性分析，检验数据的正态分布》一文中，将会继续介绍探索性分析中的检验正态性功能。如需获取下一节内容，可前往IBM SPSS Statistics中文网站。