论文：Few-Shot Knowledge Graph Completion 个人翻译及理解

本文主要是介绍论文：Few-Shot Knowledge Graph Completion 个人翻译及理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要

以前的KG补全方法需要每个关系有大量的训练实例（头尾实体对）。现实的情况是，大多数的关系，只有少量的训练实例。基于小样本的知识图谱补全还没有被很好的研究，所以本文提出了一个新的小样本关系学习模型FSRL：旨在从少量样本中发现新的关系。有效地从异构图形结构中捕获知识，对小样本进行表征，为每个关系参考集匹配相似的实体对，在两个公共数据集上的大量实验表明，FSRL的表现出了出色的性能。

介绍

大规模的知识图，如YAGO (Suchanek, Kasneci, and Weikum 2007), NELL (Carlson et al. 2010), and Wikidata (Vrandeˇci´c and Kr¨otzsch 2014) 通常以头尾实体对（节点）以及他们的之间的关系（边）的形式表示fact。这种图结构化知识对于搜索、问答和语义网络等许多下游应用是必不可少的。然而，知识图谱以其不完整而闻名。为了使KG能够实现自动补全，许多工作(Nickel, Tresp, and Kriegel 2011; Bordes et al. 2013; Socher et al. 2013; Yang et al. 2015; Trouillon et al. 2016; Schlichtkrull et al. 2018; Dettmers et al. 2018)已经被提出通过学习现有的关系来推断缺失的关系。比如：RESCAL (Nickel, Tresp, and Kriegel 2011)利用张量分解来捕获kg中多关系数据的内在结构。TransE (Bordes et al. 2013) 将关系解释为对实体的低维嵌入的翻译操作。,最近GCN (Schlichtkrull et al. 2018)利用图神经网络建立关系结构模型。
上述方法对每个关系都需要大量的实体对。然而，在实际数据集中，关系的频率分布往往有长尾。很大一部分关系在KG中只有很少的实体对。对只有少量实体对的关系进行嵌入是重要和具有挑战性的。
鉴于上述问题，Xiong et al. (2018)提出了一种引入局部邻居编码器来学习实体嵌入的Gmatching模型，它在单样本关系推理中取得了很好的性能，但仍有一定的局限性。首先，GMatching假设所有本地邻居对实体嵌入的贡献相等，然而异质邻居可能有不同的影响。因此，GMatching的邻域编码器学习到的图结构表示不足，损害了模型的性能。第二，GMatching是在单样本学习的设置下设计的。虽然它可以通过在参考集上添加一个池层来修改为小样本学习的设定，但这一操作忽略了少镜头参考实例之间的交互，限制了参考集的表示能力。为了解决上述不足之处，我们提出了一个小样本关系学习模型(FSRL)。为了学习一个匹配函数，该函数可以有效地推断出给定每个关系的一组小样本参考实体对集的真实实体对（即预测的可能存在该关系的实体对）。首先，我们提出了一种关系感知的异构邻居编码器来学习实体嵌入，它基于异构图形结构和注意机制，既能捕获到不同关系类型的信息又能捕获到本地邻居的不同影响。接下来，我们设计了一个循环自动编码器聚合网络来建模小样本实体对的交互。并为为每个关系进行累积编码。随着参考集的聚合嵌入，我们最终采用匹配网络来发现相似的关系实体对。采用基于元训练的梯度下降方法对模型参数进行优化。所学习的模型可以进一步应用于推断任何新关系的真实实体对，而不需要任何微调步骤。综上所述，我们的

主要贡献是：

1、我们介绍了一个新的小样本KG补全问题，它不同于以前的工作，更适合实际场景。
2、我们提出了一个小样本关系学习模型来解决这个问题。该模型对几个可学习的神经网络模块进行了联合优化。
3、我们对两个公共数据集进行了广泛的实验。结果表明，我们的模型优于最先进的基线模型。

准备工作

在本节中，我们正式定义了小样本知图谱补全问题，并详细说明了相应的小样学习设置。

问题定义

一个KG G 表示为三元组{(h，r，t)}⊆E×R×E，其中E和R分别表示实体集和关系集，KG补全任务是给出头实体h的和查询关系r：(h，r，？) 预测尾实体t，或者给出头部实体和尾部实体预测他们之间的不可见关系r：(h，？，t)。在这项工作中，我们做前一个任务。与之前的研究假设每个关系都有足够的实体对不同，这项工作考虑了一个实际场景，即对于每一个关系只给出了很少的实体对（参考集）。形式上，问题定义如下：

小样本知识图谱补全

给定关系r及其小样本参考实体对(hk，tk)∈Rr, 任务是设计一个机器学习模型，为每个新的头部实体h排序所有尾部候选实体t，基于实体类型约束构造候选实体集(Xiong et al. 2018),我们只考虑一组封闭的实体，即在用新的关系进行测试的阶段所涉及的实体是训练集里的实体。

小样本学习设定

这项工作的目的是设计一个机器学习模型，可以用来预测有小样本参考实例的新fact，遵循标准的少镜头学习设置(Ravi and Larochelle 2016; Snell, Swersky, and Zemel 2017)，我们设定一组训练任务，在问题中，每个训练任务对应于一个KG关系r∈R与自己的训练/测试实体对数据：Dr ={ Pr train, Pr test} ，我们将该任务集表示为元训练集Tmtr。为了模拟测试期内的小样本关系预测，每个Pr train 只包含小样本实体对，(hk, tk)∈Rr。此外Pr test = {(hi , ti , Chi,r)|(hi , r, ti) ∈ G}包含r的所有测试实体对，包括每个查询(hi，r)的真尾实体ti，和其余的候选实体tj ∈Chi,r 其中tj是G中的一个实体，因此，通过小样本参考集Pr train测试查询(hi，r)对所有候选实体进行排序，该模型可以在此集合上进行预测。我们将关系r的排名损失表示为LΘ(hi , ti|Chi,r, Pr train), 其中Θ是模型参数集。因此，模型训练的目标被定义为：
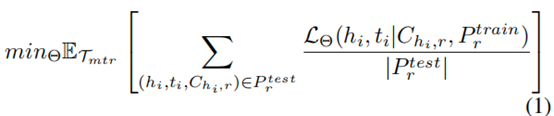
在这里插入图片描述
其中|Pr test|表示Pr test中元组的数量，下一节，我们将详细介绍如何制定和优化上述目标函数。经过充分的训练，学习到的模型可以用来预测每个新关系r0 ∈ R0的fact。这个步骤叫做元测试。元测试中的关系从元训练中是看不到的。i.e., r0∩ R0 = φ。就像元训练关系一样，元测试中的每个关系r0都有自己的少样本训练数据Pr0 train，和测试数据Pr0 test。这些关系形成了一个元测试集，它被表示为Tmte。此外，我们还留了关系集Tmtr的子集作为元验证集Tmtv，此外，该模型可以访问背景KG G0，这是G的一个子集，它排除了所有的关系Tmtr, Tmte 和 Tmtv.

模型

在这一节，我们将详细介绍FSRL的细节FSRL由三大部分组成：（1）为每个实体编码异构邻居；（2）聚合每个关系的小样本参考实体对；（3）用参考集对查询对进行匹配来做关系预测。图1显示了FSRL的框架。

编码异构邻居

虽然有许多人的工作(Nickel, Tresp, and Kriegel 2011; Bordes et al. 2013; Yang et al. 2015)已经提出通过使用关系信息来学习实体嵌入，Xiong et al. (Xiong et al. 2018) 证明了显式地编码图的局部结构有利于关系预测。所提出的邻居编码器将所有关系邻居的特征表示的平均值作为给定实体的嵌入，尽管取得较好的性能，但它忽略了异构邻居的不同影响，这可能有助于改进实体嵌入(Zhang et al. 2019)，针对这个问题，我们设计了一个具有关系感知性的异构邻居编码器。具体来说，我们给出给定头实体h的关系邻居集(关系，实体) Nh = {(ri , ti)|(h, ri , ti) ∈ G0},其中G0是背景知识图（迁移学习里的要迁移的知识），ri和ti表示h的第i个关系和相应的尾部实体，异构的邻域编码器应该能够通过考虑关系邻居的不同影响(ri , ti) ∈ Nh来编码Nh，并输出h的特征表示。为了实现这一目标，我们引入了一个注意力模块，并制定了h的嵌入如下：
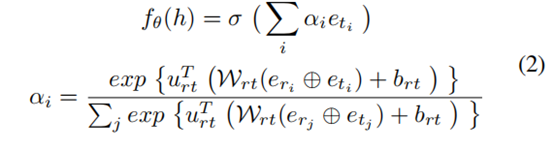
在这里插入图片描述
其中，σ表示激活单元（我们使用Tanh），⊕表示连接运算符, eti , eri ∈ Rd×1，(d：预先训练的嵌入维度)是Ti和Ri预训练的的向量。此外，, urt ∈ Rd×1, Wrt ∈ Rd×2d 和brt ∈ Rd×1 都是可学习的参数。图1(B)说明了异构邻居编码器的细节。。根据等式2，的fθ(h)公式通过注意力权重αi考虑异构关系邻居的不同影响，并利用实体ti和关系ri来计算αi。
在这里插入图片描述

聚合小样本参考集

目前的模型，无法在参考集中建模小样本实例的交互，这限制了模型的能力。我们需要设计一个模块来有效地制定每个关系r的参考集Rr的聚合嵌入。通过将邻居编码器fθ(H)应用于每个实体对(HK，tk)∈Rr，我们可以得到实体对(hk、tk) 的表示Ehk,tk=[fθ(hk)⊕fθ(tk)]。学习参考集Rr与小样本实体对的表示是具有挑战性的，因为它需要建模不同实体对之间的交互，并积累它们的表达能力。灵感来自于在学习句子嵌入方面的常见实践 (Conneau et al. 2017) 在自然语言处理和聚合节点嵌入(Hamilton, Ying, and Leskovec 2017) 在图神经网络中。我们解决了这个挑战，并通过聚合Rr中所有实体对的表示来表示Rr的嵌入：
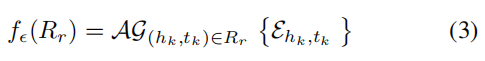
在这里插入图片描述
其中AG是一个聚合函数，可以是池化操作、前馈神经网络等。最近，递归神经网络聚合器在有序不变问题（如图嵌入）中取得了成功(Hamilton, Ying, and Leskovec 2017), 我们设计了一种实现良好能力的循环自动编码器聚合器。具体地，实体对嵌入Ehk、tk∈Rr被依次输入到递归自动编码器中：
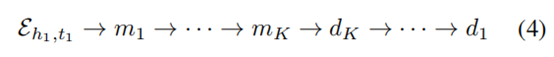
在这里插入图片描述
其中，K是参考集的大小（即小样本大小）。编码器和解码器的隐藏状态mk和dk的计算方法为：

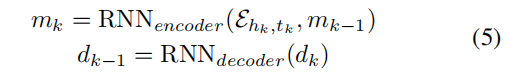
其中，RNNencoder和RNNdecoder解码器分别表示循环编码器和解码器，(e.g., LSTM (Hochreiter and Schmidhuber 1997)), 优化自动编码器的重建损失定义为：
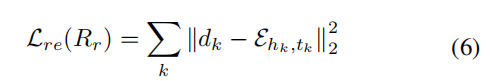
在这里插入图片描述
Lre将被用到关系排序loss中，用于细化每个实体对的表示，我们稍后将会阐述。为了建模参考集的嵌入信息，我们聚合编码器的所有隐藏状态并且通过添加残差连接和注意力机制来扩展它们，形式上， fe(Rr)的计算方法为：
在这里插入图片描述
其中uR ∈ Rd×1, WR ∈ Rd×2d 和bR ∈ Rd×1 (d：聚合嵌入维度) 是学习参数。图1©说明了递归自动编码器聚合器的细节。fe(Rr)公式聚合了Ehk、tk∈Rr的所有表示，本模块中的每个组件都将使得模型获得更好的性能，正如我们将在消融研究实验中展示的那样。

匹配查询对和参考集

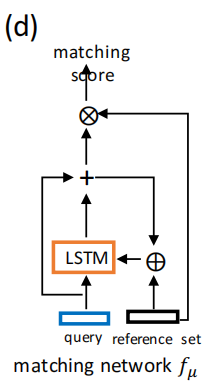
通过使用异构邻居编码器fθ和引用集聚合器fe，我们现在介绍如何有效地匹配每个查询实体对(hl , tl) ∈ Qr (Qr是关系r的所有查询对的集合) 与引用集Rr一起使用。通过将fθ和fe应用于查询实体对(hl、tl)和引用集Rr，我们可以分别得到两个嵌入向量Ehl,tl = [fθ(hl) ⊕ fθ(tl)] and fe(Rr), 为了测量两个向量之间的相似性，我们使用了一个递归处理器(Vinyals et al. 2016) fµ执行多步匹配。第t个过程步骤制定为：
在这里插入图片描述
其中，RNNmatch是LSTM单元格(Hochreiter and Schmid huber 1997), 具有输入Ehl,tl隐藏状态gt和单元格状态ct。在T“处理”步骤之后的最后一个隐藏状态gT作为查询对(hl，tl)的处理后的嵌入。我们使用Ehl,tl和fe(Rr)之间的内积作为相似性评分。图(d)显示了匹配处理器的结构。本模块可以有效地提高模型性能，我们将在消融研究实验中证明。
在这里插入图片描述

目标函数和模型训练

对于查询关系r，我们随机抽取一组少数正（真）实体对{(hk, tk)|(hk, r, tk) ∈ G}，
在这里插入图片描述
并将它们视为参考集Rr, 其余正实体对PEr = {(hl , tl)|(hl , r, tl) ∈ G ∩ (hl , tl) ∉Rr} 用作正查询对。此外，我们还通过通过污染尾部实体构造了一组负（假）实体对N Er = {(hl , t_l^- )|(hl , r, t_l^- ) /∈ G}。因此，排名损失被表述为：
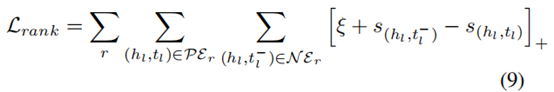
在这里插入图片描述
其中[x]+= max[0, x]是标准铰链损失，而ξ是安全边缘距离，s(hl，tl)和s(hl，t_l^{-)是查询对(hl，tl/t_l}-)和参考集Rr之间的相似性评分。通过利用参考集聚合器的重构损失小值，我们将最终目标函数定义为：

其中γ是Lrank和Lre之间的权衡因子。我们将每一种关系作为一项任务，设计了一种基于批量抽样的元训练过程。Algorithm 1中总结了这个过程的细节。