本文主要是介绍python实现三消游戏(消消乐)算法--简单案例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言:
三消算法首要实现的就是找到所有三个或三个以上的同样颜色,所以我们思路是:判断每个点进行上下左右四个方向移动后,能得到三个及以上的相连。
经过分析,当我们向一个方向移动时,会有四种情况符合条件,所以当一个点符合消除时,需要判断周围点的情况共有16种!
例如:当红色圈向右移动一格能消除时,他周围的情况必然时图下四种状态:
1.与右边两个绿圈消除
2.与右上方两个蓝圈消除
3.与右下方两个黄圈消除
4.与右边上下各一个绿色正方形消除。

所以,我们的要做的是:
第一步:
将图片转换成矩阵:
list_ = [["绿", "红", "红", "紫", "绿", "紫", "蓝"],["紫", "紫", "绿", "黄", "绿", "蓝", "紫"],["紫", "红", "紫", "红", "紫", "蓝", "黄"],["蓝", "紫", "紫", "蓝", "黄", "紫", "绿"],["红", "蓝", "绿", "紫", "黄", "蓝", "绿"]]
第二步:
从上往下,从左往右,遍历每一个点,并且遍历它周围的特定位置,判断是否移动该点,能和周围的点结合实现消除。

用于算法计算的坐标轴:

第三步:
代码实现:
list_ = [["绿", "红", "红", "紫", "绿", "紫", "蓝"],["紫", "紫", "绿", "黄", "绿", "蓝", "紫"],["紫", "红", "紫", "红", "紫", "蓝", "黄"],["蓝", "紫", "紫", "蓝", "黄", "紫", "绿"],["红", "蓝", "绿", "紫", "黄", "蓝", "绿"]]# 横坐标为x,纵坐标为y
def main_method(list_):for x in range(7):for y in range(5):# 获取该坐标点的颜色c = list_[y][x]print(x, y, c)# 判断该坐标向右移是否满足(考虑越界问题,需判断坐标变换后是否在矩阵内)if ((y - 1) >= 0 and (x + 1) <= 6 and (y + 1) <= 4 and list_[y - 1][x + 1] == c and list_[y + 1][x + 1] == c) or ((x + 2) <= 6 and (x + 3) <= 6 and list_[y][x + 2] == c and list_[y][x + 3] == c) or ((y - 1) >= 0 and (x + 1) <= 6 and (y - 2) >= 0 and list_[y - 1][x + 1] == c and list_[y - 2][x + 1] == c) or ((y + 1) <= 4 and (x + 1) <= 6 and (y + 2) <= 4 and list_[y + 1][x + 1] == c and list_[y + 2][x + 1] == c):print("请将[%s,%s]右移" % (x, y))return [x, y, '右移']# 判断该坐标向左移是否满足elif ((y - 1) >= 0 and (x - 1) >= 0 and (y + 1) <= 4 and list_[y - 1][x - 1] == c and list_[y + 1][x - 1] == c) or ((x - 2) >= 0 and (x - 3) >= 0 and list_[y][x - 2] == c and list_[y][x - 3] == c) or ((y - 1) >= 0 and (x - 1) >= 0 and (y - 2) >= 0 and list_[y - 1][x - 1] == c and list_[y - 2][x - 1] == c) or ((y + 1) <= 4 and (x - 1) >= 0 and (y + 2) <= 4 and list_[y + 1][x - 1] == c and list_[y + 2][x - 1] == c):print("请将[%s,%s]左移" % (x, y))return [x, y, '左移']# 判断该坐标向上移是否满足elif ((y - 1) >= 0 and (x - 1) >= 0 and (x + 1) <= 6 and list_[y - 1][x - 1] == c and list_[y - 1][x + 1] == c) or ((y - 2) >= 0 and (y - 3) >= 0 and list_[y - 2][x] == c and list_[y - 3][x] == c) or ((y - 1) >= 0 and (x - 1) >= 0 and (x - 2) >= 0 and list_[y - 1][x - 1] == c and list_[y - 1][x - 2] == c) or ((x + 1) <= 6 and (x + 2) <= 6 and (y - 1) >= 0 and list_[y - 1][x + 1] == c and list_[y - 1][x + 2] == c):print("请将[%s,%s]上移" % (x, y))return [x, y, '上移']# 判断该坐标向下移是否满足elif ((y + 1) <= 4 and (x - 1) >= 0 and (x + 1) <= 6 and list_[y + 1][x - 1] == c and list_[y + 1][x + 1] == c) or ((y + 2) <= 4 and (y + 3) <= 4 and list_[y + 2][x] == c and list_[y + 3][x] == c) or ((y + 1) <= 4 and (x - 1) >= 0 and (x - 2) >= 0 and list_[y + 1][x - 1] == c and list_[y + 1][x - 2] == c) or ((x + 1) <= 6 and (x + 2) <= 6 and (y + 1) <= 4 and list_[y + 1][x + 1] == c and list_[y + 1][x + 2] == c):print("请将[%s,%s]下移" % (x, y))return [x, y, '下移']else:print("不满足")continuereturn ['无有效移动']if __name__ == '__main__':main_method(list_)
运行结果:(起始坐标点为[0,0])
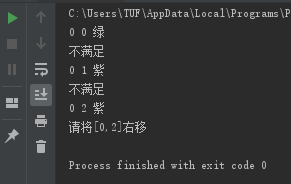
这篇关于python实现三消游戏(消消乐)算法--简单案例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





