本文主要是介绍【浅析华容道之二】华容道问题搜索求解策略,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
求解华容道问题,需要补充人工智能的一些基础知识
举一个例子介绍状态空间表示法及搜索策略
倒水问题
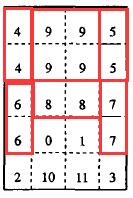
有容积为3和10的瓶子各一个,如何只用这2个瓶子从水龙头里取得4升的水?
答案:10-3-3 =4
用状态空间表示法描述如下:
对于两个瓶子,瓶里的水初始都为0,目标是第二个瓶子有4升水
初始状态(0,0)
目标状态(X,4)
搜索操作:
1. 把A瓶水倒入B:Pour_A_B
2. 把B瓶水倒入A:Pour_B_A
3. 把A注满水:Fill_A
4. 把B注满水: Fill_B
5. 把A倒空:Empty_A
6. 把B倒空:Empty_B

搜索求解策略
搜索的概念
在搜索中需要解决的基本问题
- 搜索过程中是否一定能找到一个解
- 找到一个解时,是否为最优解
- 时间与空间复杂度如何
- 搜索过程是否终止运行或是会陷入一个死循环
状态空间的搜索策略
状态空间表示法是知识表示的一种基本方法,利用状态变量和操作符号,表示系统或问题的有关知识的符号体系。状态空间可以用一个四元组表示。
基本定义:
1. 状态(State): 描述问题在任一时刻所处状况的一种数据结构
2. 初始状态S0/目标状态集G
3. 操作(Operator): 状态之间的转换函数
4. 状态空间(State Space): 四元组(S,O,S0,G)
搜索的分类
盲目搜索:在特定问题不具有任何相关信息的条件下,按固定的步骤进行搜索,它能快速调用一个操作算子
启发式搜索:考虑特定问题领域可应用的知识,动态地确定调用操作算子的步骤。优先选择较合适的操作算子,尽量减少不必要的搜索,以尽快到达目标状态。
盲目搜索有:深度优先搜索、广度优先搜索
启发式搜索一般优于盲目搜索
《————————————————–我是分割线—————————————————》
求解华容道
搜索策略
盲目搜索: 按预定方向进行搜索
输入:
- 初始状态S0/目标状态集G
- 操作(Operator): 状态之间的转换函数
输出:
- 一组状态序列
算法思路:见流程图,为了防止重复搜索或陷入循环,建立如下两个表
Closed列表: 存储已展开过的状态——避免重复搜索
Open列表: 存储已生成但未展开的状态——实现回溯
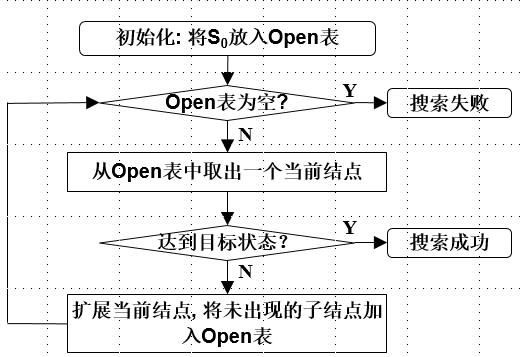
宽度优先搜索: Open表先进先出
深度优先搜索: Open表先进后出
扩展当前节点:找出某个状态的所有相邻状态(即移动一步可到达的状态),未出现的子节点放入Open表
数据结构
- 二维数组
可将棋子编号固定为:0,1,2,3表示四个刘备兵,4,5,6,7,8表示五虎将,9表示曹操,有必要时将两个空格也看作两个棋子,编号为10,11.这样棋盘的布局可用一个5行4列的二维数组来表示.
判断是否为目标布局:
仅需判断该数组中的第四,五行中的第二、三列元素的取值是否都等于9.
算法优化
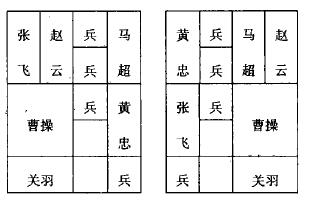
- 同质:
棋盘上任意两个相同形状、相同摆放的棋子是”同质”的,在计算机看来没有任何区别。如图:
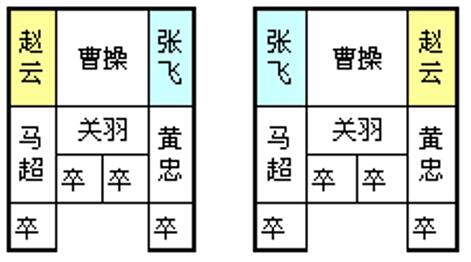
- 对称
如下图,每一种状态下的任一种走法对另一种状态来说只要左右移动与之相反即可得到相应的走法。因此在求解华容道问题时可将下图两个状态视为相同状态。
程序设计
广度优先搜索
广度优先搜索表现出来的是一种谨慎,它按照一种同心圆的方式,首先访问所有和初始节点邻接的节
点,然后是离它的节点最近的所有未访问节点,依此类推,直到所有与初始节点在一个连通分量中的节点
都访问过了为止。最优解
对华容道问题,棋子每走一步是对当前节点生成它的一个子节点,在走法的步数最少为最优的意义下,寻找它的最优解实际上也就是寻找路径最短的解.因此,只要某种初始布局存在解,则应用广度优先搜索策略总是可以搜索到它的最优解。在进行广度优先搜索时,一个盘面状态可以理解为一个节点。深度优先不适合求解华容道问题,当然可以按一定策略调整搜索方法,深度搜索和广度搜搜结合或采用启发式算法进行搜索。
下一篇讲解启发式算法提高搜索效率。
这篇关于【浅析华容道之二】华容道问题搜索求解策略的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!