【GAMES101】Lecture05 Rasterizaion 1 (Triangles) 光栅化之三角形

本文主要是介绍【GAMES101】Lecture05 Rasterizaion 1 (Triangles) 光栅化之三角形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0 引言
1 MVP后要做什么呢？
- 1.1 MVP是什么
- 1.2 Canonical Cube to Screen 标准立方体到屏幕
- 1.3 Rasterizing Triangles into Pixels 将三角形光栅化为像素
2 Rasterization：Drawing to Raster Display
- 2.1 Polygon Meshes
- 2.2 Triangle Meshes
- 2.3 Triangles - Fundamental Shape Primitives 基本形状基元
3 A Simple Approach: Sampling 采样：简单的光栅化方法

请添加图片描述

🙋‍♂️ 作者：海码007
📜 专栏：计算机图形学专栏
💥 标题：【GAMES101】Lecture05 Rasterizaion 1 (Triangles) 光栅化之三角形
❣️ 寄语：对知识永远有兴趣！
🎈 最后：文章作者技术和水平有限，如果文中出现错误，希望大家能指正

0 引言

在进行了上一课所学的内容后，模型物体全都都被映射到【-1， 1】的区间里，那下一步该怎么办呢？也就是光栅化。

透视投影

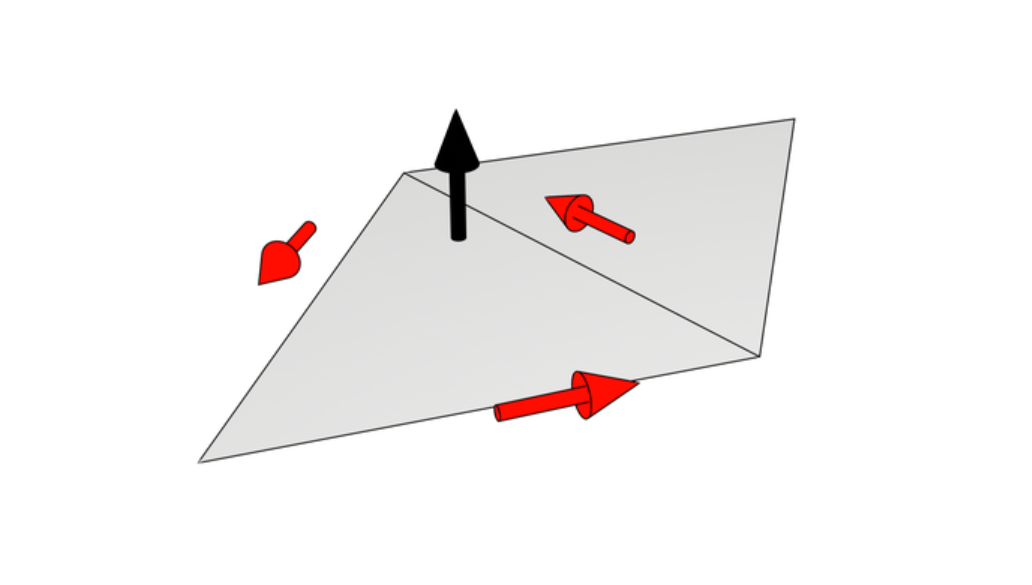
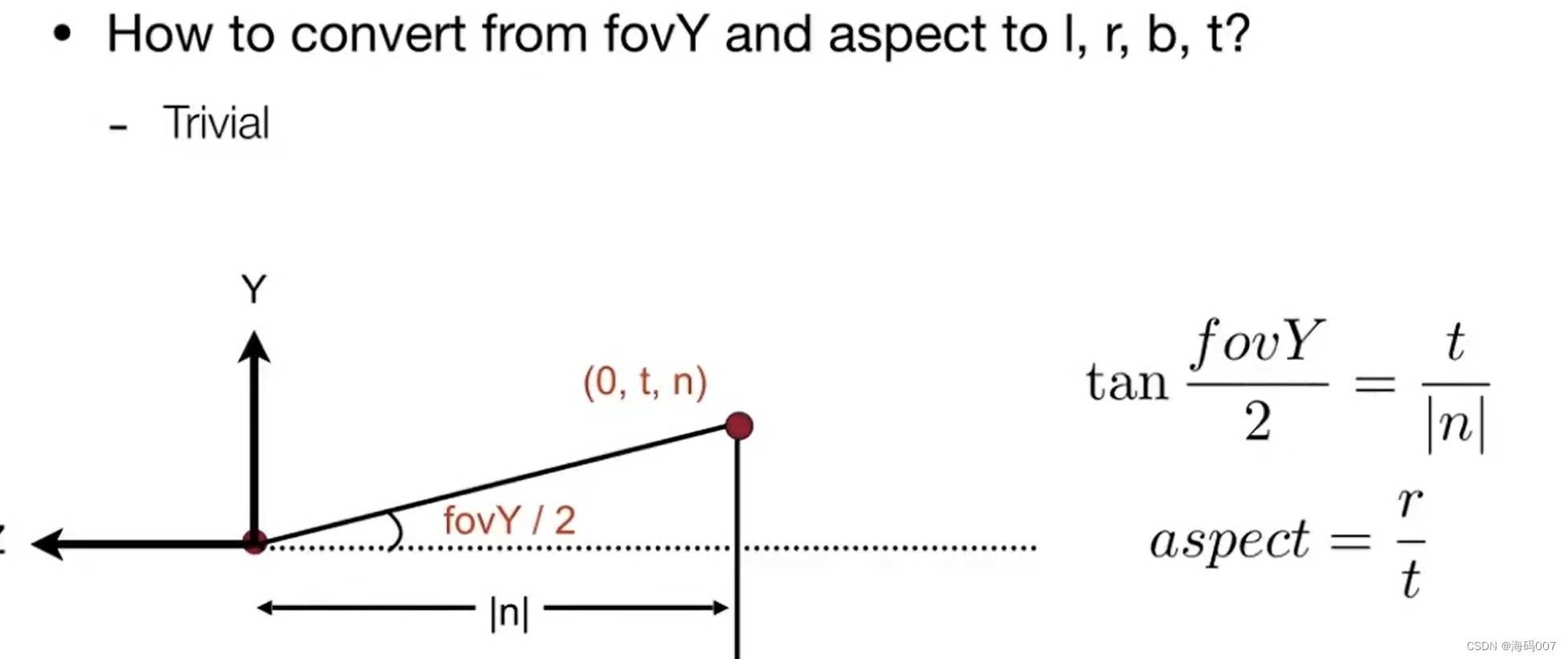
近裁剪平面的l、r、b、t分别代表左、右、底、顶。它们定义了视锥体在近裁剪平面上的四个边界。
FOV代表视场角（Field of View），是指从相机或眼睛位置观察场景时，能够看到的水平和垂直范围。通常以角度为单位来表示，较大的FOV意味着更广阔的视野，而较小的FOV则意味着更窄的视野。 FOV的大小直接影响到观察者在场景中的感知和交互体验。
FOV（Field of View）是指从相机或眼睛位置观察场景时，能够看到的水平和垂直范围的角度。而FOVY（Field of View Vertical）是FOV的一个子集，专指在垂直方向上能够看到的范围的角度。FOV包含了水平和垂直两个方向的视野范围，而FOVY只关注垂直方向上的视野范围。

要将FOVY（垂直视场角）转换为裁剪平面的边界值（l、r、b、t），您需要考虑相机的投影方式以及近裁剪平面的位置。

假设您使用的是透视投影（perspective projection），可以使用以下步骤将FOVY转换为裁剪平面的边界值：

首先，根据FOVY计算出近裁剪平面（near plane）上的一半高度（h_near）。

( h_{\text{near}} = \tan\left(\frac{\text{FOVY}}{2}\right) \times \text{near} )

其中，( \text{near} ) 是近裁剪平面的距离。
然后，根据相机的纵横比（aspect ratio）计算出近裁剪平面上的一半宽度（w_near）。

( w_{\text{near}} = h_{\text{near}} \times \text{aspect ratio} )

其中，aspect ratio是屏幕或视口的宽度与高度之比。
最后，使用这些计算出的宽度和高度值来确定裁剪平面的边界值：
- 左边界（l）：( -w_{\text{near}} )
- 右边界（r）：( w_{\text{near}} )
- 底边界（b）：( -h_{\text{near}} )
- 顶边界（t）：( h_{\text{near}} )

这样，您就可以将FOVY转换为近裁剪平面的边界值。

在这里插入图片描述

1 MVP后要做什么呢？

1.1 MVP是什么

MVP代表Model View Projection，是计算机图形学中常用的一种矩阵变换顺序，用于将模型的顶点坐标变换到裁剪空间（Clip Space）中，从而实现透视投影和最终的屏幕显示。MVP变换由三个矩阵相乘组成：

Model Matrix（模型矩阵）：将模型的局部坐标系变换到世界坐标系中，包括平移、旋转和缩放等操作。
View Matrix（视图矩阵）：将世界坐标系中的坐标变换到观察者（相机）的视图空间中，通常包括相机的位置和方向。
Projection Matrix（投影矩阵）：将视图空间中的坐标变换到裁剪空间中，进行透视投影或正交投影，通常包括视场角、纵横比、近裁剪平面和远裁剪平面等参数。

MVP变换的顺序是先将模型的顶点坐标乘以模型矩阵，再乘以视图矩阵，最后乘以投影矩阵，得到裁剪空间中的坐标。这个过程通常在图形渲染管线的顶点着色器中完成。
在这里插入图片描述