本文主要是介绍基于最小二乘递推算法的系统参数辨识matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
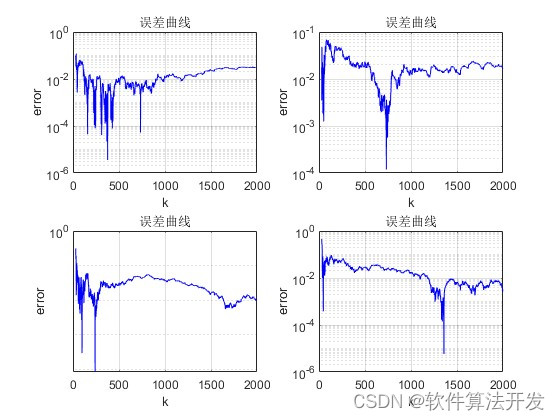
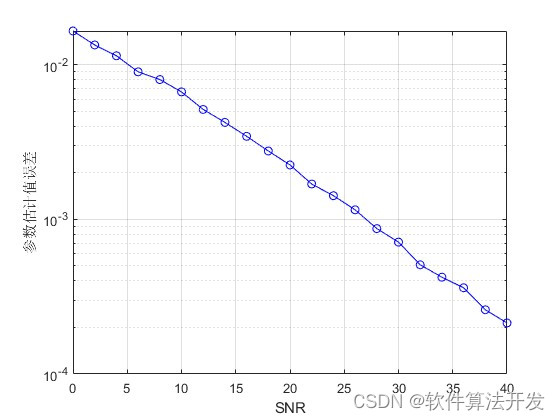
基于最小二乘递推算法的系统参数辨识。对系统的参数a1,b1,a2,b2分别进行估计,计算估计误差以及估计收敛曲线,然后对比不同信噪比下的估计误差。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行

3.核心程序
................................................................for i=(LEN0+4):LENz(i,1)=-A1*z(i-1,1)-A2*z(i-2,1)+B1*Xin(i-1,1)+B2*Xin(i-2,1)+Noise(i,1); for j=1:Nz1(i-3,j) = z(N+i-3-j+idx0,1);u1(i-3,j) = Xin(N+i-3-j+idx0,1);end h =[-z1(i-3,1) -z1(i-3,2) u1(i-3,1) u1(i-3,2)]';K = P*h/(h'*P*h+1);P =(eye(2*N)-K*h')*P;Pest = Pest+K*[z(i,1)-h'*Pest];Pest2(:,i) = Pest;
endfigure
subplot(221);
k=1:LEN;
semilogy(k,e1,'b');
xlabel('k');
ylabel('error');
title('误差曲线')
grid onsubplot(222);
k=1:LEN;
semilogy(k,e2,'b');
xlabel('k');
ylabel('error');
title('误差曲线')
grid onsubplot(223);
k=1:LEN;
semilogy(k,e3,'b');
xlabel('k');
ylabel('error');
title('误差曲线')
grid onsubplot(224);
k=1:LEN;
semilogy(k,e4,'b');
xlabel('k');
ylabel('error');
title('误差曲线')
grid on
33
4.本算法原理
最小二乘递推算法是一种在线估计模型参数的方法,特别适用于实时、连续的数据流中进行系统的动态参数辨识。RLS算法的核心思想是利用最新的观测数据不断更新对系统参数的估计,以期达到最小化预测误差平方和的目的。


通过这种递推的方式,RLS可以在每次得到新的观测数据后迅速调整参数估计,并保持计算复杂度相对较低,适合实时应用场合。
5.完整程序
VVV
这篇关于基于最小二乘递推算法的系统参数辨识matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







