本文主要是介绍人工蜂群算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
人工蜂群算法
人工蜂群算法(Artificial Bee Colony Optimization,ABC)是一种基于蜜蜂觅食行为的优化算法,由土耳其学者Karaboga于2005年提出,算法模拟蜜蜂的采蜜行为对优化问题进行求解。
算法原理
ABC算法的核心思想是将优化问题的解空间视作蜜源,蜜蜂作为搜索代理在解空间中进行探索。在算法的每一轮迭代中,蜜蜂根据当前蜜源的质量和周围蜜源的信息,选择性地进行勘探和开发,从而逐步优化搜索空间。蜜源的位置代表了优化问题的可能解决方案,蜜源的花蜜量对应于相关解决方案的优劣,ABC算法与优化问题的对应关系如下表所示。
| ABC | 优化问题 |
|---|---|
| 蜜源 | 可行解: X i = ( x i 1 , x i 2 , … , x i D ) X_i=(x_{i1},x_{i2},\dots,x_{iD}) Xi=(xi1,xi2,…,xiD) |
| 花蜜量 | 适应度 |
算法超参数
ABC算法的超参数包括雇佣蜂比例和蜜源保留次数阈值等,参数影响着蜜蜂在搜索空间中的行为和搜索效率。
- e m p l o y e d _ r a t e employed\_rate employed_rate:雇佣蜂比例;
- l i m i t limit limit:蜜源保留次数的阈值;
- NP:种群大小;
- Gmax:最大迭代数。
寻优公式
人工蜂群由雇佣蜂(employed bees)、围观蜂(onlookers)和侦察蜂(scouts)三类蜜蜂组成。在标准的ABC算法中,蜂群的前半部分由受雇的人工蜜蜂组成,后半部分为观察蜂。每个蜜源只有一只雇佣蜂,受雇蜜蜂的数量等于蜂巢周围食物源的数量。被雇用的蜜蜂的食物源已被蜜蜂吃光,它就会转变为侦察蜂探索新的蜜源。ABC通过重复执行雇佣蜂、观察蜂和侦察蜂三个阶段来寻找问题的最优解。
- 雇佣蜂阶段,雇佣蜂在现有蜜源的位置开发新的蜜源。
v i j t = x i j t + ϕ i j t ( x i j t − x k j t ) (1) v_{ij}^t=x_{ij}^t + \phi_{ij}^t(x_{ij}^t - x_{kj}^t) \tag{1} vijt=xijt+ϕijt(xijt−xkjt)(1)
其中, k ∈ { 1 , ⋯ , N P } k \in \{1,\cdots,NP\} k∈{1,⋯,NP}且 k ≠ i k\neq i k=i, ϕ i j ∈ [ − 1 , − 1 ] \phi_{ij} \in [-1,-1] ϕij∈[−1,−1]。
X i t + 1 = { X i t , if f i t ( X i ) t > f i t ( V i t ) V i t + 1 , e l s e (2) X_{i}^{t+1}= \begin{cases} X_{i}^t, & \text{if $fit(X_i)^t > fit(V_i^t)$}\\ V_{i}^{t+1},& else \end{cases} \tag{2} Xit+1={Xit,Vit+1,if fit(Xi)t>fit(Vit)else(2) - 观察蜂阶段,观察蜂对雇佣蜂分享的蜜源信息进行分享,采用轮盘赌策略来选址蜜源跟踪开采新的蜜源,公式与式(1)等价。
- 侦察蜂阶段,蜜源 X i X_i Xi拥有参数trial,统计蜜源没有被更新的次数,当蜜源更新被保留时,trail设置为0;反之,trail加1。如果一个蜜源经过多次开采没被更新,当trail超过了阈值limit,那么需要抛弃该蜜源,启动侦察探索新的蜜源。
x i j = x i , j m i n + r a n d ( 0 , 1 ) ⋅ ( x i , j m a x − x i , j m i n ) (3) x_{ij}=x_{i,j}^{min}+rand(0,1) \cdot (x_{i,j}^{max} - x_{i,j}^{min}) \tag{3} xij=xi,jmin+rand(0,1)⋅(xi,jmax−xi,jmin)(3)
雇佣蜂阶段和观察蜂阶段体现了算法的开发过程即算法对已知优质解的利用,侦察蜂阶段体现了算法的探索过程即算法对新解的探索。
初始化
初始解应当覆盖整个搜索空间,一般采用均匀分布随机生成初始解。
x i j 0 = x i , j m i n + r a n d ( 0 , 1 ) ⋅ ( x i , j m a x − x i , j m i n ) (4) x_{ij}^0=x_{i,j}^{min}+rand(0,1) \cdot (x_{i,j}^{max} - x_{i,j}^{min}) \tag{4} xij0=xi,jmin+rand(0,1)⋅(xi,jmax−xi,jmin)(4)
其中,rand(0,1)表示0-1之间的随机数, x i j m a x x_{ij}^{max} xijmax和 x i j m i n x_{ij}^{min} xijmin分别表示该问题第j个维度变量的上下界。
伪代码
输入:超参数 ( e m p l o y e d _ r a t e , l i m i t , N P , G m a x ) (employed\_rate,limit,NP,Gmax) (employed_rate,limit,NP,Gmax)和搜索边界 X m i n X_{min} Xmin, X m a x X_{max} Xmax
输出:最优解
1:初始化
2:根据式(4)初始化位置种群X
3:记录群体最优gbest
4:优化搜索
5:For G = 1:Gmax
6: \qquad 雇佣蜂更新
7: \qquad 观察蜂更新
8: \qquad 侦察蜂更新
9: \qquad 更新群体最优 g b e s t gbest gbest
10:End
注:优化算法并不保证能够得到问题的最优解,因此,算法输出的最优解并非问题的整体最优解,而是搜索过程中最好的一个解。
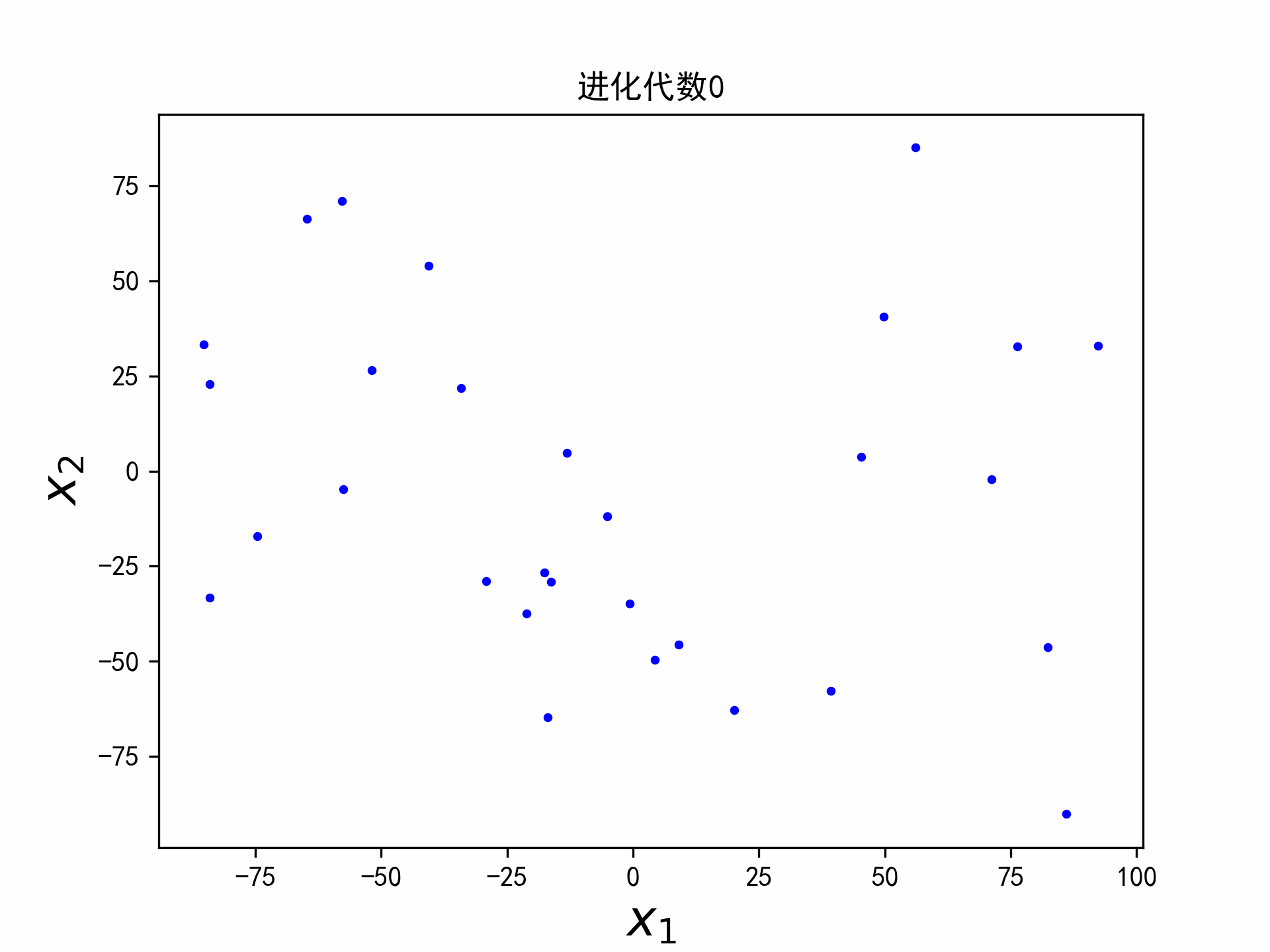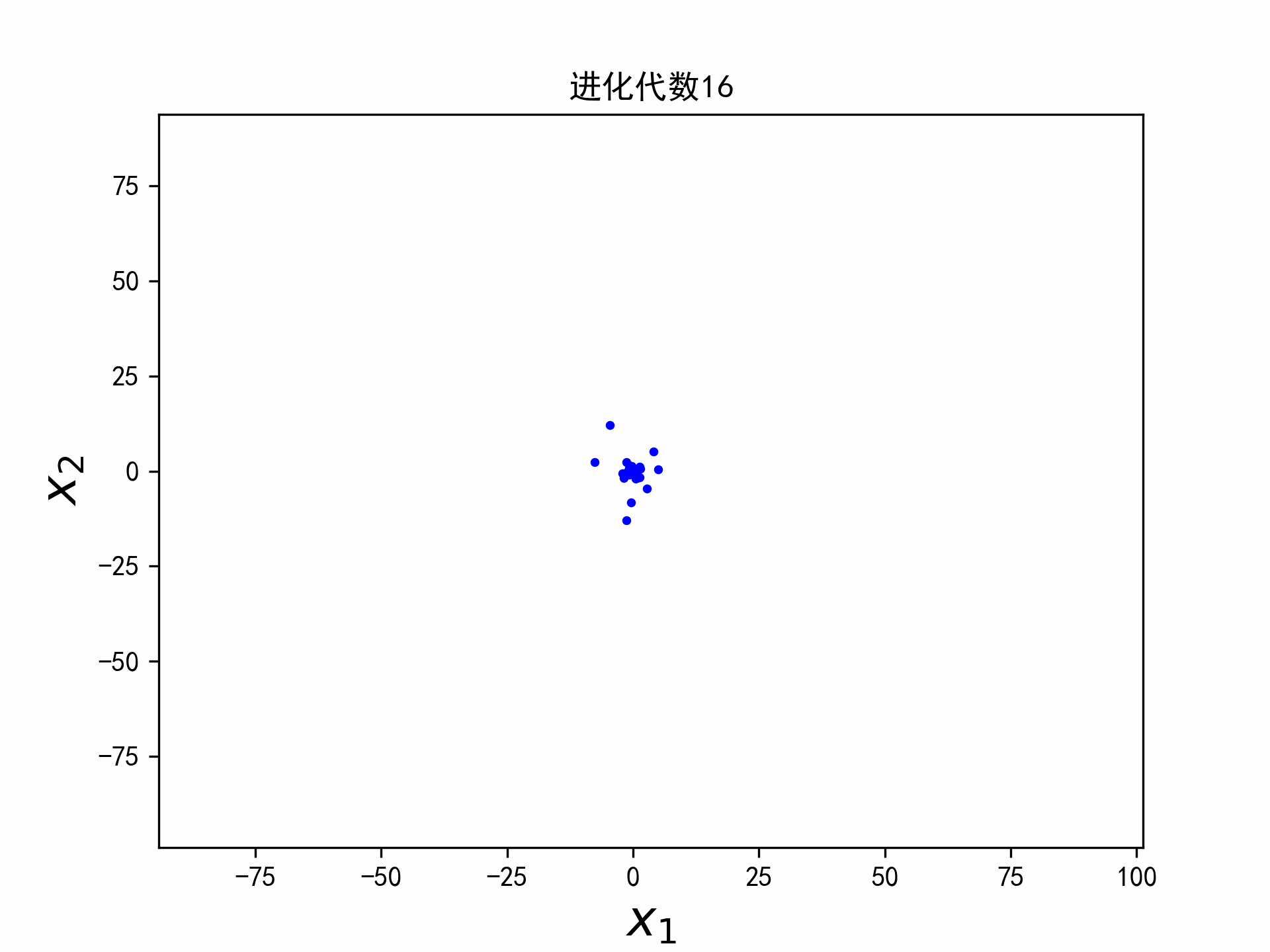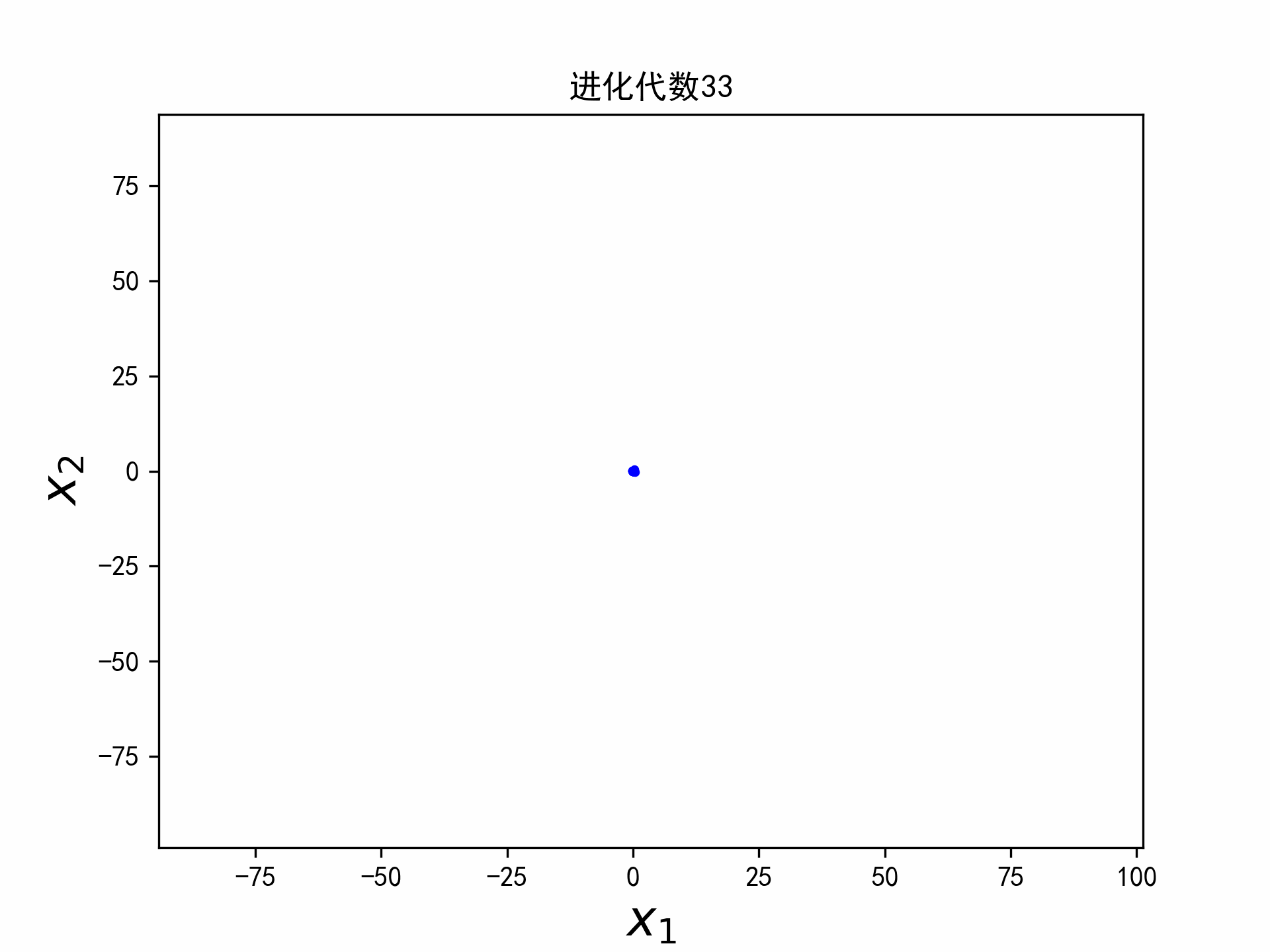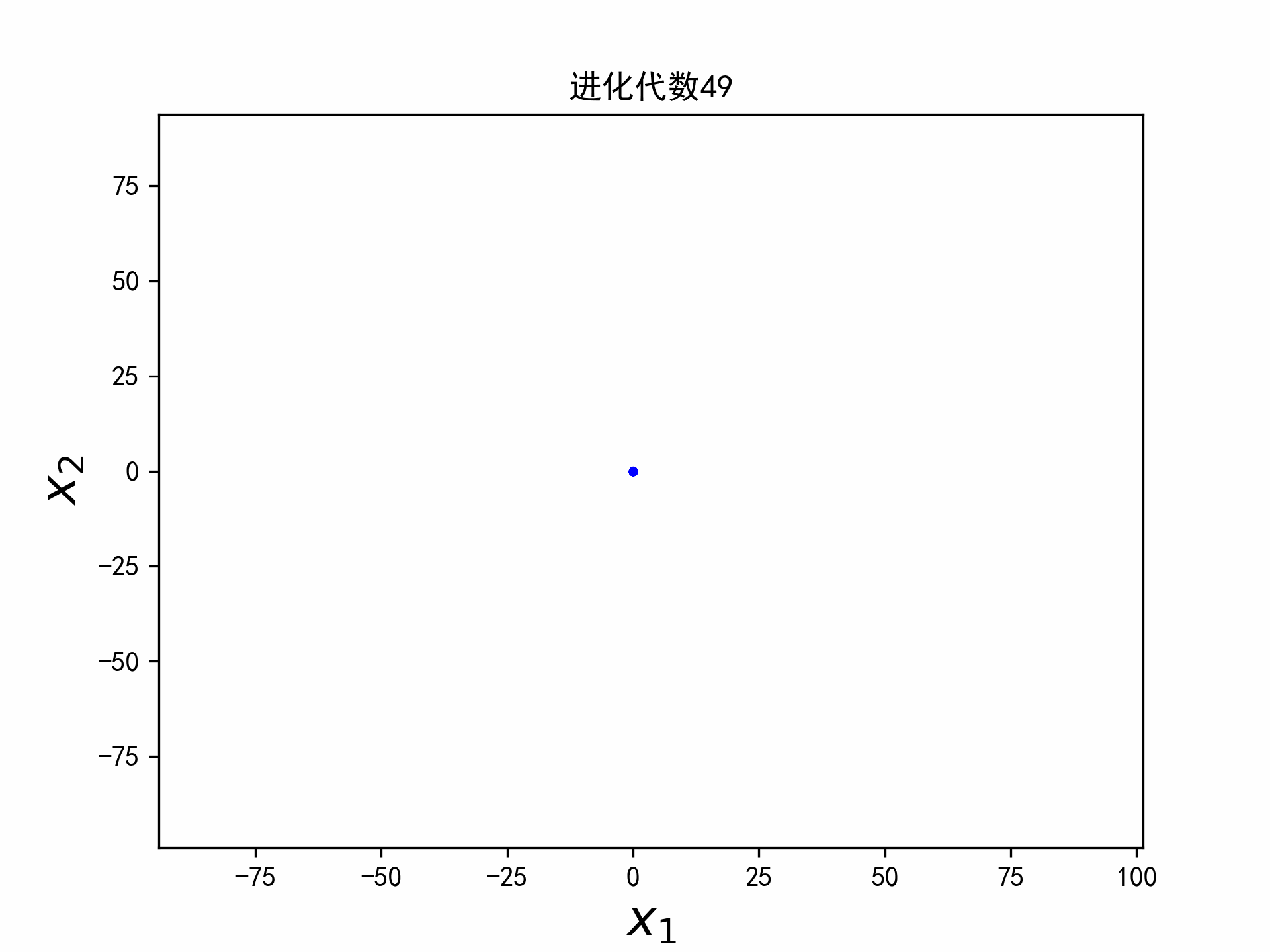
实验
实验选取二维的平方和函数,函数的最小值在点(a,b)取得,最小值为0。
f ( x 1 , x 2 ) = ( x 1 − a ) 2 + ( x 2 − b ) 2 (5) f(x_1,x_2) = (x_1 - a)^2 + (x_2-b)^2 \tag{5} f(x1,x2)=(x1−a)2+(x2−b)2(5)
实验参数如下:
| 参数 | 值 |
|---|---|
| 问题维度D | 2 |
| 种群数NP | 30 |
| 最大进化次数Gmax | 50 |
| 雇佣蜂比例 | 0.5 |
| limit | 10 |
| 取值范围 | (-100,100) |

| 最优值 | 最差值 | 平均值 | 标准差 |
|---|---|---|---|
| 1.686e-11 | 5.679e-7 | 6.952e-8 | 1.324e-7 |
代码获取
关注微信公众号数学模型与算法回复 ABC算法获取python代码

参考文献
[1] 何尧,刘建华,杨荣华.人工蜂群算法研究综述[J].计算机应用研究,2018,35(05):1281-1286.
[2] Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical report-tr06, Erciyes university, engineering faculty, computer engineering department, 2005.
[3] Akay B, Karaboga D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information sciences, 2012, 192: 120-142.
这篇关于人工蜂群算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








