Python算法题集_搜索二维矩阵

本文主要是介绍Python算法题集_搜索二维矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文为Python算法题集之一的代码示例

题51：搜索二维矩阵

1. 示例说明

• 给你一个满足下述两条属性的 m x n 整数矩阵：

  • 每行中的整数从左到右按非严格递增顺序排列。
  • 每行的第一个整数大于前一行的最后一个整数。

  给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

  示例 1：

  

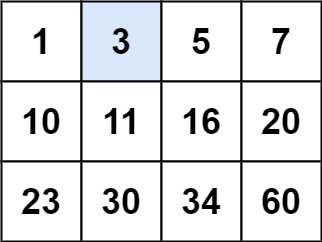
  输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
  输出：true
  

  示例 2：

  

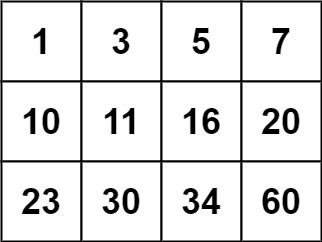
  输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
  输出：false
  

  提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -104 <= matrix[i][j], target <= 104

---

2. 题目解析

- 题意分解

1. 本题是在已排序二维矩阵中查找目标数字
2. 最快方式就是二分法

- 优化思路

1. 通常优化：减少循环层次

2. 通常优化：增加分支，减少计算集

3. 通常优化：采用内置算法来提升计算速度

4. 分析题目特点，分析最优解

   1. 本题的已排序二维矩阵可以连成排序一维列表，实现一维列表二分法

   2. 本题的二维矩阵首尾可以连成排序一维列表，定位具体行之后，在具体行中再进行二分查找

   3. 可以考虑使用排序列表操作模块bisect

- 测量工具

• 本地化测试说明：LeetCode网站测试运行时数据波动很大【可把页面视为功能测试】，因此需要本地化测试解决数据波动问题
• CheckFuncPerf（本地化函数用时和内存占用测试模块）已上传到CSDN，地址：Python算法题集_检测函数用时和内存占用的模块
• 本题本地化超时测试用例自己生成，详见章节【最优算法】，代码文件包含在【相关资源】中

---

3. 代码展开

1) 标准求解【矩阵展开为列表+二分法】

将矩阵展开为列表，再通过二分法查找目标数值是否存在

页面功能测试，马马虎虎，超过53%

import CheckFuncPerf as cfpclass Solution:def searchMatrix_base(self, matrix, target):if not matrix:return Falseimaxrow, imaxcol, listval = len(matrix), len(matrix[0]), []for iIdx in range(len(matrix)):listval.extend(matrix[iIdx])ileft, iright = 0, len(listval) - 1while ileft <= iright:imid = (iright - ileft) // 2 + ileftif target == listval[imid]:return Trueif target < listval[imid]:iright = imid - 1else:ileft = imid + 1return FalseaSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_base, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 searchMatrix_base 的运行时间为 12768.90 ms；内存使用量为 467828.00 KB 执行结果 = True

2) 改进版一【行*列区间二分法】

将下标换算为行*最大列数+列，将矩阵换算为0 -> 行 * 列的线性区间，在这个区间通过二分法查找目标数值是否存在

页面功能测试，马马虎虎，超过33%

import CheckFuncPerf as cfpclass Solution:def searchMatrix_ext1(self, matrix, target):if not matrix:return Falseimaxrow, imaxcol = len(matrix), len(matrix[0])ileft, iright = 0, imaxrow * imaxcol - 1while ileft <= iright:imid = (ileft + iright) // 2mid_row, mid_col = imid // imaxcol, imid % imaxcolif matrix[mid_row][mid_col] == target:return Trueelif matrix[mid_row][mid_col] < target:ileft = imid + 1elif matrix[mid_row][mid_col] > target:iright = imid - 1return FalseaSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_ext1, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 searchMatrix_ext1 的运行时间为 0.00 ms；内存使用量为 12.00 KB 执行结果 = True

3) 改进版二【第三方模块】

将矩阵展开为列表，再使用排序列表操作模块bisect来查找插入位置

页面功能测试，性能一般，超过82%

import CheckFuncPerf as cfpclass Solution:def searchMatrix_ext2(self, matrix, target):if not matrix:return Falseimaxrow, imaxcol, listval = len(matrix), len(matrix[0]), []for iIdx in range(len(matrix)):listval.extend(matrix[iIdx])from bisect import bisect_leftipos = bisect_left(listval, target)if ipos == imaxrow * imaxcol:return Falsereturn listval[ipos] == targetaSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_ext2, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 searchMatrix_ext2 的运行时间为 0.00 ms；内存使用量为 12.00 KB 执行结果 = True

---

4. 最优算法

根据本地日志分析，最优算法为第2种方式【行*列区间二分法】searchMatrix_ext1

本题测试数据，似乎能推出以下结论：

1. 二分法查询性能非常夸张，简直是瞬间定位【1亿的数组，1毫秒定位】
2. 数据的迁移【从矩阵->列表】耗时耗内存，这也是大数据兴起的原因之一【数据的迁移代价远高于计算代价】
3. 第三方模块的函数消耗内存非常小

import random
imaxrow, imaxcol, istart = 10000, 10000, 0
mapnums = [[0 for x in range(imaxcol)] for y in range(imaxrow)]
for irow in range(imaxrow):for icol in range(imaxcol):istart += random.randint(0, 6)mapnums[irow][icol] = istart
itarget = mapnums[imaxrow//2][imaxcol//2]
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_base, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_ext1, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(aSolution.searchMatrix_ext2, mapnums, itarget)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 算法本地速度实测比较
函数 searchMatrix_base 的运行时间为 12768.90 ms；内存使用量为 467828.00 KB 执行结果 = True
函数 searchMatrix_ext1 的运行时间为 0.00 ms；内存使用量为 12.00 KB 执行结果 = True
函数 searchMatrix_ext2 的运行时间为 6336.15 ms；内存使用量为 1508.00 KB 执行结果 = True

---

5. 相关资源

本文代码已上传到CSDN，地址：Python算法题源代码_LeetCode(力扣)_搜索二维矩阵

一日练，一日功，一日不练十日空

may the odds be ever in your favor ~

这篇关于Python算法题集_搜索二维矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---