【动态规划.3】[IOI1994]数字三角形 Number Triangles

本文主要是介绍【动态规划.3】[IOI1994]数字三角形 Number Triangles，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

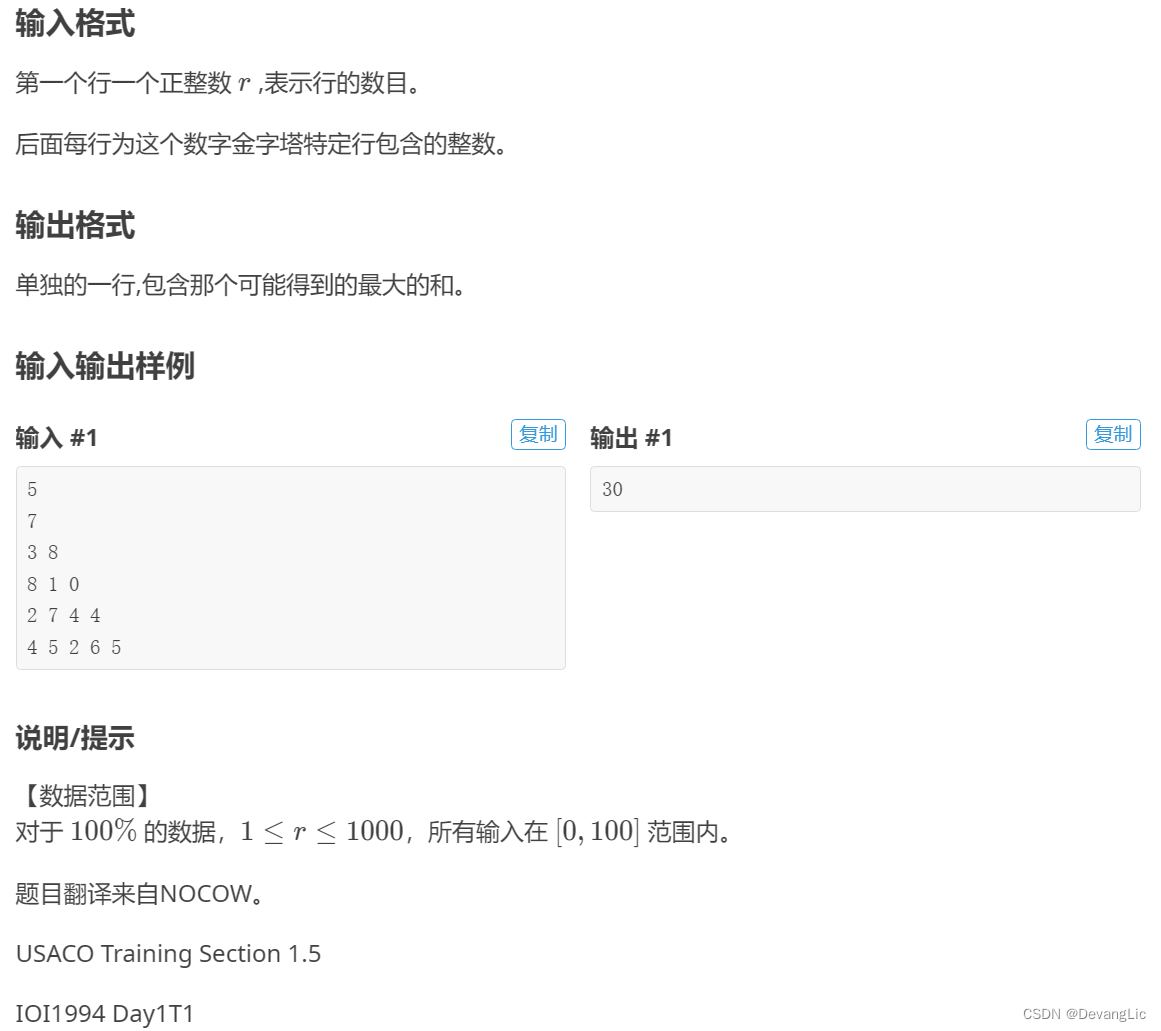
题目

https://www.luogu.com.cn/problem/P1216

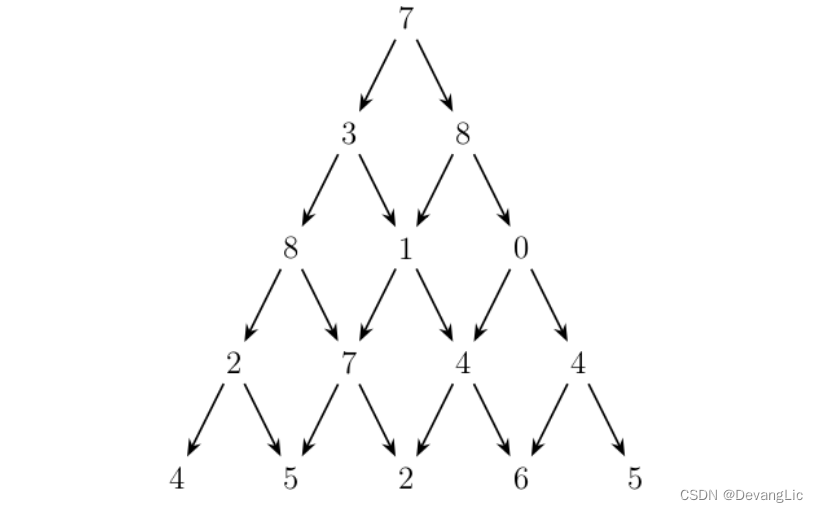
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

7→3→8→7→5 的路径产生了最大权值。

分析

这是一个动态规划的入门期。题目。在我们拿到这个题的时候。我们不妨想一想其中的一个数字，比方说第二行的。第5行，第1个数字。他往下会有怎么样的走法。啊，他没法走因为下边已经没有数字了。别慌，我们换一种思路来分析。我们往上面走，倒着来看。
5’‘
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
在原始的基础上不妨新设一个二维的数组。在原先的位置上将放上他们路径产生的和。
因为一个数字不会成为和，那么至少有两个数字嘛，我们就从倒数第二行开始分析。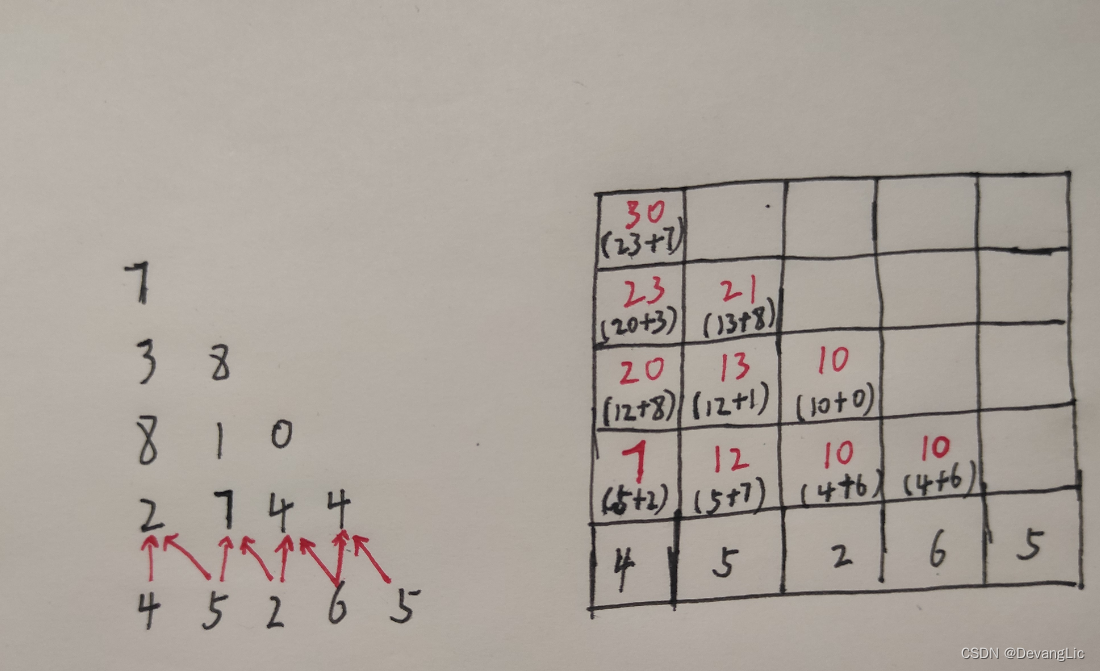
在这个图片上，红色数字所代表的都是当前位置的最优值。那么最顶端的那一个也就是我们想要的最大的值了，因为它是两个初级最优值之和 。即 dfs(1,1)

代码

#include <bits/stdc++.h>  
//  2024-03-08  Come on !
using namespace std;  
#define  ll long long 
const int N=1005;
ll n  , D[N][N] ,b[N][N];
int  dfs(int x1,int y1){if(x1>n || y1>n)  return 0;else return max(dfs(x1+1,y1),dfs(x1+1,y1+1))+D[x1][y1];
}
/*
不妨把自上而下叫做 望路模式 —— 一个十分小心精明的人
自下而上 ：叫做  回忆模式 ，在回忆中推理出最大的/最小的 
*/
int main() {  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // no endll;  int t=1;while(t--){int i,j;cin>>n;for(i=1;i<=n;i++)for(j=1;j<=i;j++)cin>>D[i][j];//solve();cout<<dfs(1,1);}return 0;  
}

这篇关于【动态规划.3】[IOI1994]数字三角形 Number Triangles的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---