对神经网络的理解，以及代码的手动实现，以鸾尾花数据集为例

“”"

这是一个神经网络的示意图。

大家看到这里可能会感到非常的困惑，什么输入层，输出层，隐藏层，权重，阈值什么的到底是什么。接下来我为大家举个例子，去理解它。
这里我们从线性回归开始一步步引入神经网络，因为我们可以把线性回归看成是一个单层的神经网络，它的结构就应该是这样：

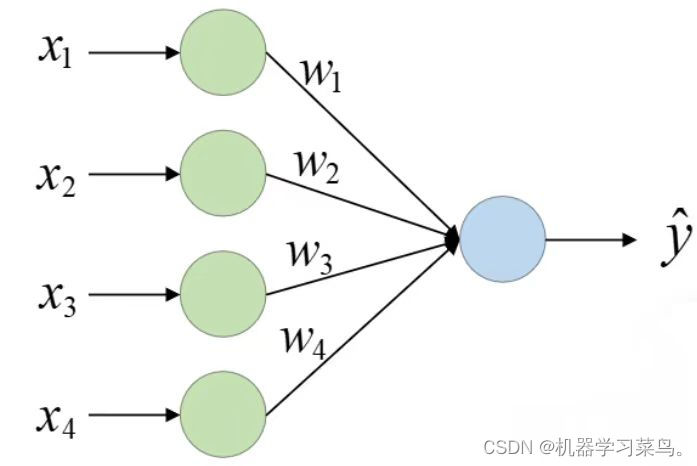
在线性回归中，我们尝试使用一条y_pred=wx+b的直线来拟合真实值y_true。使用梯度下降来一步步逼近他的真实的结果，也就是求出与真实值最接近的[w,b]来拟合最终结果，如下图所示

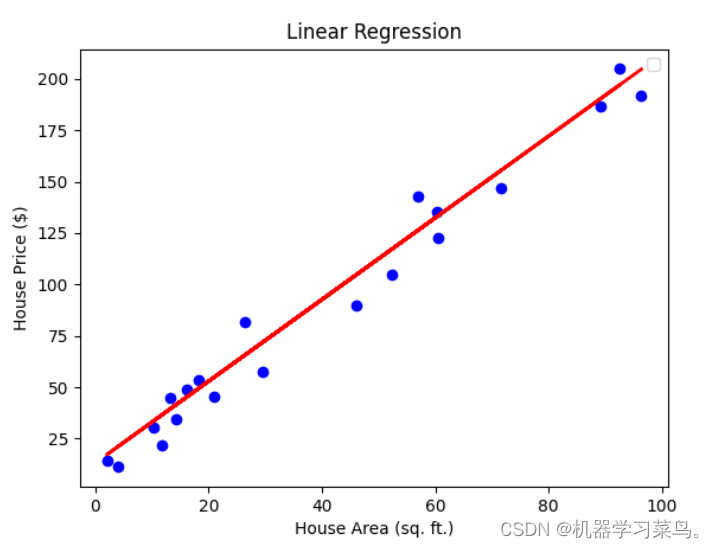
但是当我们数据之间的关系是非线性的时候，例如这样：

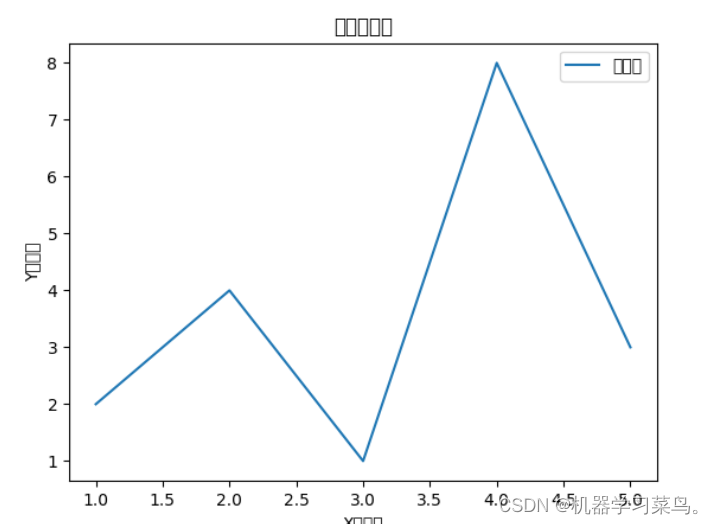
我们就无法通过一条直线来拟合它，这时候，我们可以尝试为他的结构中加入隐藏层，例如这样：

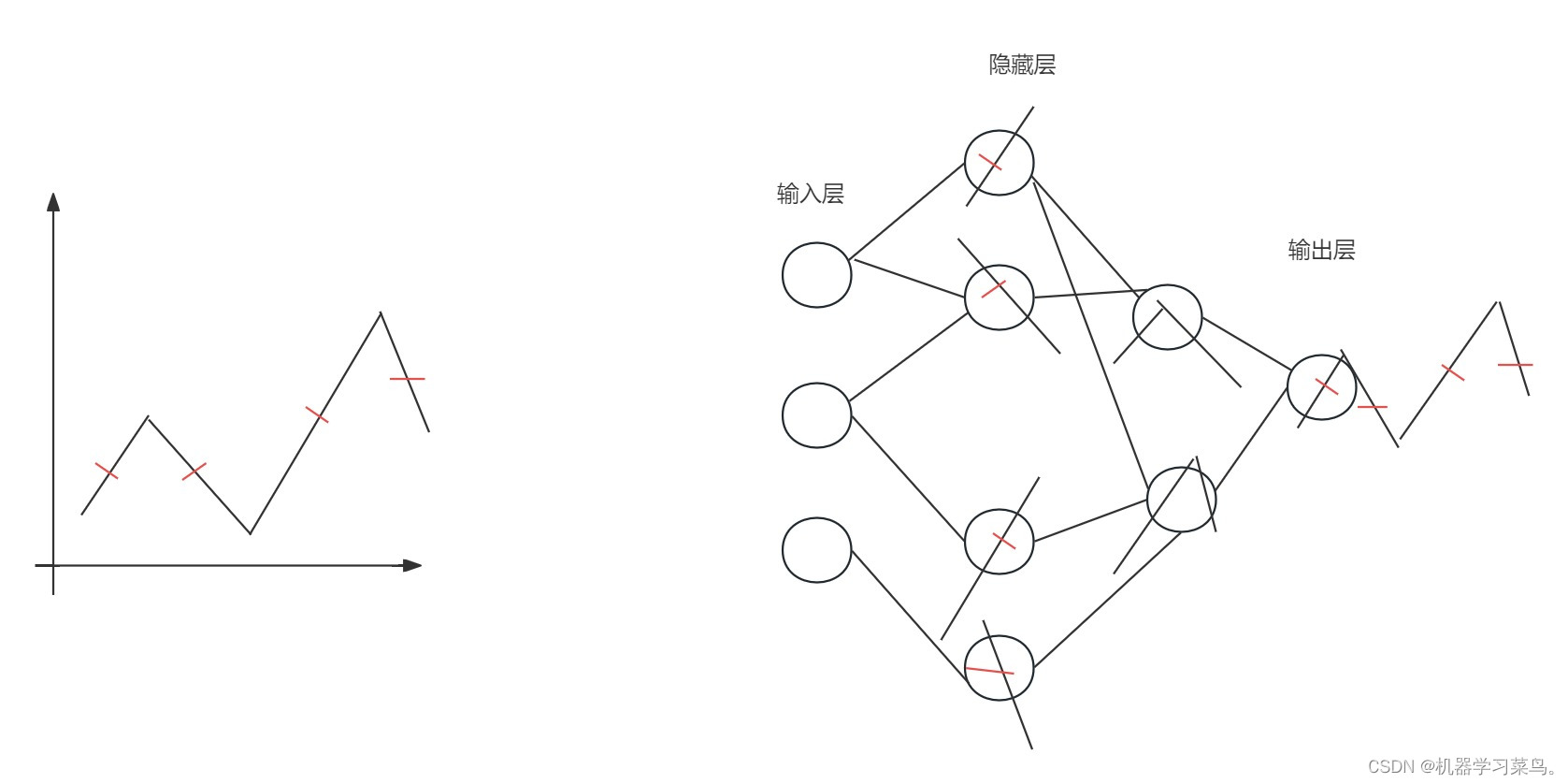
通过每一个隐藏层神经元来模拟它的每一条直线，第一个隐藏层学到单方向的直线，第二个隐藏层将两条线拼接，以此类推直到最后都拼接起来。这样我们就能完全模拟它的规律了，也就是能拟合出一个非线性的y。

从上边我们就可以得到这样一个结论：在神经网络中，当数据线性不可分的时候才需要隐藏层。

那么问题来了，隐藏层的数量和每个隐藏层中神经元的数量应该为多少呢？·········这里我们可以把它理解为一个可以调整的超参数。

想要确定神经网络中隐藏层的数量和每个隐藏层中神经元的数量是一个关键的问题，对于神经网络的性能和训练效果有重要影响。这个问题通常没有一个通用的答案，取决于具体的任务和数据。这里是一些我的建议。
简单任务： 对于相对简单的任务，例如基本的图像分类或回归问题，可以尝试只使用一个隐藏层。
复杂任务： 对于更复杂的任务，如图像识别、自然语言处理等，可能需要深层网络，即多个隐藏层。深度神经网络通常能够学习到更复杂的特征和表示。
避免过拟合： 大型神经网络可能会导致过拟合，尤其是在训练数据有限的情况下。可以使用正则化技术、丢弃（Dropout）等方法来防止过拟合。
尝试不同的配置： 尝试不同的隐藏层神经元数量的配置，使用交叉验证来评估模型性能，选择效果最好的配置。

接下来我们尝试代码实现。

当把神经网络理解为，加入隐藏层的线性回归，我们在梯度下降的时候，就可以使用以下四个步骤

这里提到了线性回归，对线性回归的理解我们可以参考我的上一篇文章：
想要实现神经网络应该从以下四个步骤开始
1.先随机初始化一个权重和阈值

#初始化权重，以及阈值
weight_input_hidden=np.random.uniform(size=(input_layer_number,hidden_layer_number))
bias_hidden=np.random.uniform(size=(1,hidden_layer_number))
weight_hidden_output=np.random.uniform(size=(hidden_layer_number,output_layer_number))
bias_output=np.random.uniform(size=(1,output_layer_number))

开始梯度下降：

2.前向传播
1.输入层到隐藏层：
定义变量 hidden_layer_input，含义为隐藏的输入，对输入层输入的数据乘以输入层到隐藏层的权重再加上隐藏层阈值bias，这里实际上就是使用y=wx+b来拟合最终结果

 hidden_layer_input=np.dot(X_train,weight_input_hidden)+bias_hidden

再用激活函数sigmod（）把数据映射到（0，1）区间上
这里hidden_layer_output为隐藏层的输出

  hidden_layer_output=sigmoid(hidden_layer_input)

2.隐藏层到输出层：对输入层映射过来的数据乘以权重w再加上输出层的阈值bias然后把它通过激活函数sigmod（）映射到（0，1）区间上

  	output_layer_input=np.dot(hidden_layer_output,weight_hidden_output)+bias_outputoutput_layer_output=sigmoid(output_layer_input)

3。计算误差
使用目标值y减去输出层的输出，得到误差

error=y_train-output_layer_output

4.反向传播
（1）计算输出层的误差对结果的贡献程度，用于调整隐藏层到输出层的权重，d_output表示输出层每个单元的局部梯度
（2） 定义变量error_hidden 表示隐藏层整体的误差，用于计算隐藏层的权重的梯度，
（3）用于调整输入层和隐藏层的权重，d_hidden 表示隐藏层中每个单元的局部梯度

	d_output=error*derivative_sigmoid(output_layer_output)error_hidden=d_output.dot(weight_hidden_output.T)d_hidden=error_hidden*derivative_sigmoid(hidden_layer_output)

5.更新权重和偏置
1.隐藏层到输出层的权重=原始权重+学习率a*（隐藏层的输出乘输出层每个单元的局部梯度）
主要是为了更新了连接隐藏层和输出层的权重矩阵，根据隐藏层的输出、输出层的局部梯度和学习率来调整权重，以减小输出层的误差。
2.输出层的阈值就等于原始阈值+学习率a*（输出层局部梯度之和）
主要是为了更新了输出层的偏差项，根据输出层的局部梯度和学习率来调整偏差项，以减小输出层的误差
3.输入层到隐藏层的权重=原始权重+学习率a*（输入样本乘隐藏层每个单元的局部梯度）
主要是为了更新了连接输入层和隐藏层的权重矩阵，根据输入数据、隐藏层的局部梯度和学习率来调整权重，以减小隐藏层的误差
4.隐藏层的阈值就等于原始阈值+学习率a*（隐藏层局部梯度之和）
主要是为了更新隐藏层的偏差项，根据输出层的局部梯度和学习率调整偏差，以减小隐藏层的误差。

	weight_hidden_output+=learning_rate*np.dot(hidden_layer_output.T,d_output)bias_output+=np.sum(d_output,axis=0,keepdims=True)*learning_rateweight_input_hidden+=learning_rate*np.dot(X_train.T,d_hidden)bias_hidden+=np.sum(d_hidden,axis=0,keepdims=True)*learning_rate

以下是完整代码，写的不好没有使用函数式编程的写法，但是便于理解一点，使用我上面的步骤可以很方便的实现它：

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
# 导入鸾尾花数据集
iris=datasets.load_iris()
X=iris.data
print(X)
y=iris.target# 使用one-hot对类别进行独热编码
num_class=len(np.unique(y))
y_one_hot=np.eye(num_class)[y]#划分数据
X_train,X_test,y_train,y_test=train_test_split(X,y_one_hot,test_size=0.2,random_state=1)# 定义激活函数
def sigmoid(x):return 1/(1+np.exp(-x))#定义激活函数的导数
def derivative_sigmoid(x):return x*(1-x)#定义输入层，隐藏层，以及输出层的个数
input_layer_number=4
hidden_layer_number=8
output_layer_number=num_class#初始化权重，以及阈值
weight_input_hidden=np.random.uniform(size=(input_layer_number,hidden_layer_number))
bias_hidden=np.random.uniform(size=(1,hidden_layer_number))
weight_hidden_output=np.random.uniform(size=(hidden_layer_number,output_layer_number))
bias_output=np.random.uniform(size=(1,output_layer_number))#定义超参数
learning_rate=0.001
epochs=100001
for epoch in range(1,epochs):#前向传播hidden_layer_input=np.dot(X_train,weight_input_hidden)+bias_hiddenhidden_layer_output=sigmoid(hidden_layer_input)output_layer_input=np.dot(hidden_layer_output,weight_hidden_output)+bias_outputoutput_layer_output=sigmoid(output_layer_input)#计算误差error=y_train-output_layer_output# 反向传播d_output=error*derivative_sigmoid(output_layer_output)error_hidden=d_output.dot(weight_hidden_output.T)d_hidden=error_hidden*derivative_sigmoid(hidden_layer_output)# 更新权重和偏置weight_hidden_output+=learning_rate*np.dot(hidden_layer_output.T,d_output)bias_output+=np.sum(d_output,axis=0,keepdims=True)*learning_rateweight_input_hidden+=learning_rate*np.dot(X_train.T,d_hidden)bias_hidden+=np.sum(d_hidden,axis=0,keepdims=True)*learning_rateif(epoch%1000==0):print("模型训练{0}次的结果是{1}".format(epoch,np.mean(np.abs(error))))
#模型训练结束，使用测试集对模型进行测试
hidden_layer_input = np.dot(X_test, weight_input_hidden) + bias_hidden
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, weight_hidden_output) + bias_output
output_layer_output = sigmoid(output_layer_input)predicted_class = np.argmax(output_layer_output, axis=1)
print(predicted_class)
true_class = np.argmax(y_test, axis=1)
accuracy = np.mean(predicted_class == true_class)
print(f'Test Accuracy: {accuracy * 100}%')

我们来看看代码跑出来的结果：

可以看到我们的误差为0.032，而分类的精准度为100%。