本文主要是介绍刨析数据结构(三),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
🌈个人主页:小田爱学编程
🔥 系列专栏:数据结构-带你无脑刨析
🏆🏆关注博主,随时获取更多关于IT的优质内容!🏆🏆
😀欢迎来到小田代码世界~
😁 喜欢的小伙伴记得一键三连哦 ૮(˶ᵔ ᵕ ᵔ˶)ა

目录
一.算法效率
时间复杂度
空间复杂度
二.时间复杂度
1.如何计算
计算方法:
2.结果:O(N的二次方)
2.常见复杂度举例
三.空间复杂度
1.如何计算
2.常见复杂度举例
四.OJ题
1.
分析思路:
代码实现
分析思路:
代码实现:
2.
分析思路:
代码实现:
一.算法效率
🚀时间复杂度
🚀空间复杂度
二.时间复杂度
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)//N次
{for (int j = 0; j < N ; ++ j)//N次{++count;}
}for (int k = 0; k < 2 * N ; ++ k)//2N次
{++count;
}
int M = 10;
while (M--)//10次
{++count;
}
printf("%d\n", count);
}🌏时间的复杂度:

1.如何计算
计算方法:
🔥大O的渐进表示法:大O符号(Big O notation):是用于描述函数渐进行为的数学符号
1 、用常数 1 取代运行时间中的所有加法常数。2 、在修改后的运行次数函数中,只保留最高阶项。3 、如果最高阶项存在且不是 1 ,则去除与这个项目相乘的常数。得到的结果就是大 O 阶。
2.结果:O(N的二次方)
2.常见复杂度举例
1.
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}执行了2N+10次->根据大O的渐进表示法->结果为O(N)
2.
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}执行了N+M次->O(M+N)次
3.
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}执行了100次->O(N)
4.
const char * strchr ( const char * str, int character );// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}6
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}三.空间复杂度
void BubbleSort(int* a, int n)
{
assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}使用了常数个额外空间,所以空间复杂度为 O(1)
1.如何计算
2.常见复杂度举例
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}使用了N个额外空间,所以空间复杂度为 O(N)
3.
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
四.OJ题
1.
1.面试题 17.04. 消失的数字 - 力扣(LeetCode)
分析思路:
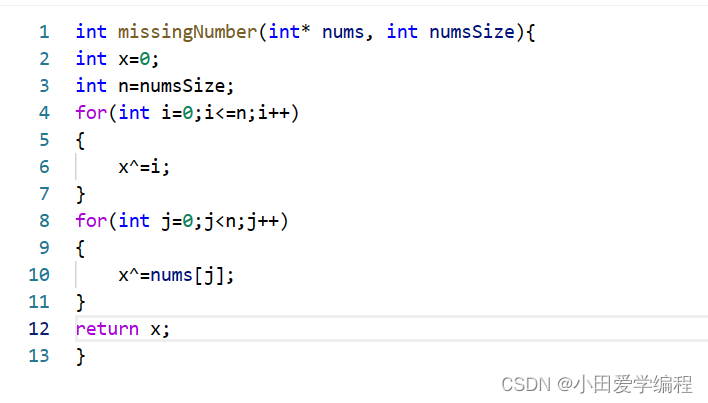
1.计算出所有数的和,然后以此减去原有的数字得到的数字就是消失的数字
代码实现
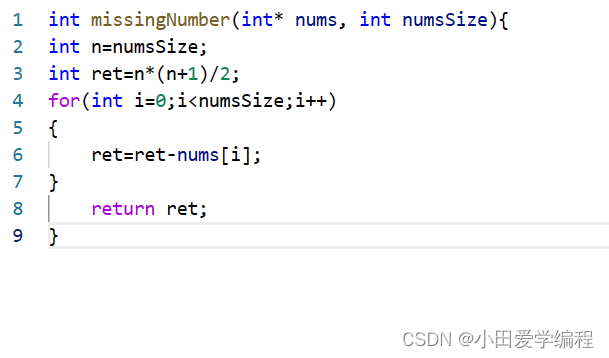
分析思路:
2.x先和0-n中的所有值异或然后与数组中的所有值异或
👨🚀史上最通俗易懂的异或运算详解【含例题及应用】-CSDN博客
代码实现:
189. 轮转数组 - 力扣(LeetCode)
2.
189. 轮转数组 - 力扣(LeetCode)189. 轮转数组 - 力扣(LeetCode)

分析思路:
代码实现:

🎁🎁🎁今天的分享到这里就结束啦!如果觉得文章还不错的话,可以三连支持一下,您的支持就是我前进的动力! 
这篇关于刨析数据结构(三)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!