代码随想录算法训练营第三十九天|动态规划|62.不同路径、63. 不同路径 II

本文主要是介绍代码随想录算法训练营第三十九天|动态规划|62.不同路径、63. 不同路径 II，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

62.不同路径

文章
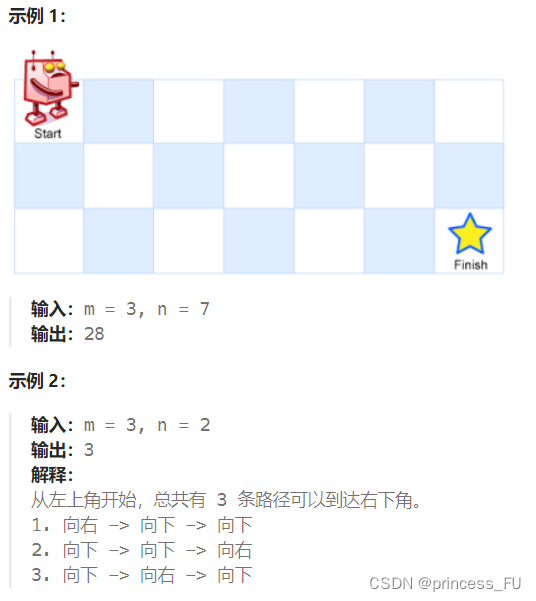
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

在这里插入图片描述
简单

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};

数论方法没看

63. 不同路径 II

文章
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

比较简单

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++){if(obstacleGrid[i][0])break;dp[i][0] = 1;}for (int j = 0; j < n; j++){if(obstacleGrid[0][j])break;dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if(obstacleGrid[i][j]) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];cout<< dp[i][j] ;}cout<<endl;}return dp[m - 1][n - 1];}
};