算法48：动态规划专练(力扣221：最大正方形面积)

本文主要是介绍算法48：动态规划专练(力扣221：最大正方形面积)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

我之前写过一篇博客，是利用单调栈计算最大矩形面积的。感兴趣的看一下：算法37：最大矩形面积(力扣84、85题)---单调栈-CSDN博客

而本道题目求的是最大正方形面积，因此，利用单调栈完全可以解决。思路和求最大矩形面积是一样的，下面直接贴出单调栈的代码：

单调栈解法:

package code04.动态规划专项训练02;/***  力扣 221题  最大正方形面积*  https://leetcode.cn/problems/maximal-square/?envType=study-plan-v2&envId=dynamic-programming*/
public class MaximalSquare_03_leetcode221单调栈 {public int maximalSquare(char[][] matrix) {if (matrix == null || matrix.length == 0) {return 0;}int[] dp = new int[matrix[0].length];int res = 0;for (int i = 0; i < matrix.length; i++) {for (int j = 0; j < matrix[i].length; j++) {//数组压缩int cur = matrix[i][j] == '0' ? 0 : Integer.parseInt(String.valueOf(matrix[i][j]));dp[j] = cur == 0 ? 0 : dp[j] + cur;}res = Math.max(res, getMaxValue(dp));}return res;}public int getMaxValue (int[] arr) {int result = 0;int size = arr.length;//自定义栈结构int[] stack = new int[arr.length];int stackSize = 0;for (int i = 0; i < arr.length; i++) {while (stackSize != 0 && arr[stack[stackSize-1]] >= arr[i]) {//当前弹出数的下标int curIndex = stack[--stackSize];//左边第一个比curIndex数组对应数小的下标int leftIndex = stackSize == 0 ? -1 : stack[stackSize -1];//右边第一个比curIndex数组对应数小的下标int rightIndex = i;int width = Math.min(arr[curIndex], rightIndex - leftIndex - 1);result = Math.max(result, width * width);}stack[stackSize++] = i;}//如果还有剩余while (stackSize != 0) {//当前弹出数的下标int curIndex = stack[--stackSize];//左边第一个比curIndex数组对应数小的下标int leftIndex = stackSize == 0 ? -1 : stack[stackSize -1];int width = Math.min(arr[curIndex], size - leftIndex - 1);result = Math.max(result, width * width);}return result;}public static void main(String[] args) {MaximalSquare_03_leetcode221单调栈 ss = new MaximalSquare_03_leetcode221单调栈();char[][] matrix = {{'1','0','1','0','0'},{'1','0','1','1','1'},{'1','1','1','1','1'},{'1','0','0','1','0'}};System.out.println(ss.maximalSquare(matrix));}
}

 

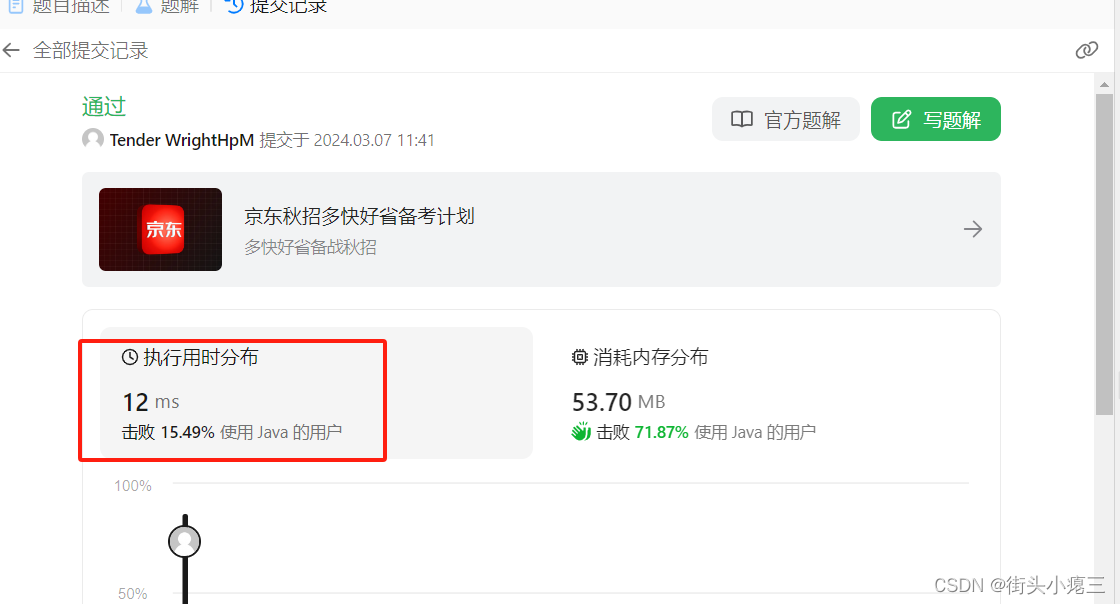
胜率虽然不高，但是只花费了 12毫秒， 还算可以的了。

本章是动态规划专练，因此，不得不说一下动态规划的思路：

1. 我们知道，正方是有4个顶点，并且每条边的边长都是相等的。

2. 本道题规定，如果每个单元格的值为1，那么它最小也可以看成是变成为1的正方形。如果为0，当前单元格就不能算作正方形。

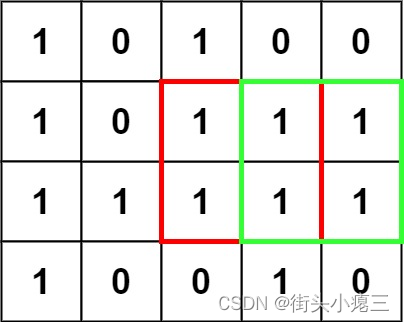
3. 如果只有4个顶点，想要组成最大边长为2的正方形，那么这4个顶点必定全部都为1.  如果以最后一个顶点为正方形的结束点，那么依赖的其他三个点，必定全部不为0.

 

X1	X3
X2	1 + Math.min(X1, Math.min(X2, X3)) (依赖左、上、左上3个顶点的最小值) 也就是说，目前看到的这些节点，以当前单元格 结束，那么它的最大边长就是1 + Math.min(X1, Math.min(X2, X3)) 为什么要依赖最小值？ 因为，X1、X2、X3任何一点为0， 那么以当前单元格为正方形的结束节点，那么它的最大正方形边长就为1. 当然，当前单元格的值必须不为0.

4. 第一行，正方形的边长最大为1； 第一列，最大正方形的边长也为1. 因为正方形边长是需要相等的。

我们根据事例1给的数据进行推导：

第一步：

	下标0	1	2	3	4
下标0	1	0	1	0	0
1	1	原始数组为0， 无法参与到正 方形的结束点. 直接取0	前一列为0， 上一列为1.取小。 当前列为1.  因此, 1 + 0 = 1	1 + 0 = 1	1 + 0 = 1
2	1
3	1

第二步：根据上方规则，类推

	下标0	1	2	3	4
下标0	1	0	1	0	0
1	1	0	1	1	1
2	1	1 + 0 = 1	1 + 1 = 2	1+ 1 = 2	1+ 1 = 2
3	1

第三步：根据上方规则，类推

	下标0	1	2	3	4
下标0	1	0	1	0	0
1	1	0	1	1	1
2	1	1	2	2	2
3	1	0	0	1+0 = 1	0

 目测就知道，最大正方形的边长为2. 面积为 4；

动态规划代码：

package code04.动态规划专项训练02;/*** 力扣 221题  最大正方形面积* https://leetcode.cn/problems/maximal-square/?envType=study-plan-v2&envId=dynamic-programming*/
public class MaximalSquare_03_leetcode221动态规划 {public int maximalSquare(char[][] matrix) {if (matrix == null || matrix.length == 0) {return 0;}int row = matrix.length;int col = matrix[0].length;int[][] dp = new int[row][col];int maxSide = 0;//第一行for (int i = 0; i < col; i++) {dp[0][i] = matrix[0][i] == '0' ? 0 : 1;if (maxSide == 0 && dp[0][i] > 0) {maxSide = 1;}}//第一列for (int i = 0; i < row; i++) {dp[i][0] = matrix[i][0] == '0' ? 0 : 1;if (maxSide == 0 && dp[i][0] > 0) {maxSide = 1;}}for (int index1 = 1; index1 < row; index1++) {for (int index2 = 1; index2 < col; index2++) {if (matrix[index1][index2] == '1') {//左上顶点int p1 = dp[index1 - 1][index2 - 1];//左顶点int p2 = dp[index1][index2 - 1];//上顶点int p3 = dp[index1 - 1][index2];dp[index1][index2] = Math.min(p3, Math.min(p1, p2)) + 1;} else {dp[index1][index2] = 0;}maxSide = Math.max(maxSide, dp[index1][index2]);}}return maxSide * maxSide;}public static void main(String[] args) {MaximalSquare_03_leetcode221动态规划 ss = new MaximalSquare_03_leetcode221动态规划();//char[][] matrix = {{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}};//char[][] matrix = {{'0', '1'}, {'1', '0'}};char[][] matrix = {{'0', '1'}};System.out.println(ss.maximalSquare(matrix));}
}

它的确比单调栈更快，效率更高。而且，它的思路更加的简单。

但是，它只能解决正方形的问题，如果是矩形，当前思路都无法解决。因此，他有一定的局限性。

下一道题，同样也是算最大正方形面积的题目。但是，单调栈、本章的动态规划推导思路完全不适用，只能用暴力方法去解决。因此，本道题的暴力方法，也必须得介绍一下。

暴力解法：

1. 遍历全部单元格，找出每个单元格作为正方形顶点的最大边长。

2. 在步骤1找的过程中，是范围内的验证。

暴力解法思路相对简单，只是代码比较复杂。

package code04.动态规划专项训练02;/*** 力扣 221题  最大正方形面积* https://leetcode.cn/problems/maximal-square/?envType=study-plan-v2&envId=dynamic-programming* <p>* 基本思路:* 1. 当前列为正方形起点。* 从左往右，推算出最大边长； 从上往下推算出最大边长； 因为是正方形，因此之前两个边长取小* 2. 对这个范围内的所有格子进行为1验证*/
public class MaximalSquare_03_leetcode221暴力解 {public int maximalSquare(char[][] matrix) {if (matrix == null || matrix.length == 0) {return 0;}int row = matrix.length;int col = matrix[0].length;//最大边长int max = 0;for (int i = 0; i < row ; i++) {//当前行的每一列都作为正方形的左上角，即起始点for (int j = 0; j < col; j++) {//当前格子是否为1,为1才可能成为正方形的起始点if (matrix[i][j] == '0') {continue;}//整个二维数组中，重要有1出现，那正方形边长至少为1if (max == 0) {max = 1;}//行边长，列边长，两者取小。因为是正方形int p = Math.min(row - i, col - j);//从i,j开始 到 i+index,j+index 范围内。全部都为1，才能验证通过//start为默认边长，默认边长为1. 因为matrix[i][j] == 1for (int count = 1; count < p; count++) {//斜线if (matrix[i + count][j+count] == '0') {break;}boolean flag = true;// 如果上边行、左边列延伸都不为0；那就继续校验正方形// 内部是否全为1for (int m = 0; m < count; m++) {if (matrix[i + count][j + m] == '0' || matrix[i + m][j + count] == '0') {flag = false;break;}}if (flag) {//默认边长为1, 即当前正方形做顶点为1//count是新增的长度。 count+1 代表正常放边长max = Math.max(max, count + 1);}else {break;}}}}return max * max;}public static void main(String[] args) {MaximalSquare_03_leetcode221暴力解 ss = new MaximalSquare_03_leetcode221暴力解();//char[][] matrix = {{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}};char[][] matrix = {{'0', '1'}, {'1', '0'}};System.out.println(ss.maximalSquare(matrix));}
}

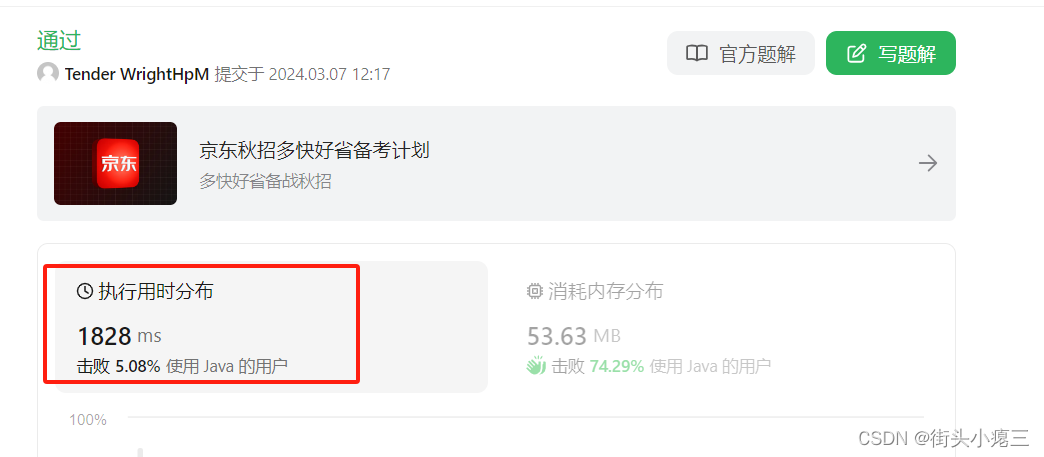
因此，本道题使用单调栈、动态规划性能更高。暴力解法，性能低。因为下一道题，只能基于暴力解法完成并优化，因此，不得不提前在此提一下暴力解法。

这篇关于算法48：动态规划专练(力扣221：最大正方形面积)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---