蓝桥杯 夺冠概率 解题报告

    足球比赛具有一定程度的偶然性，弱队也有战胜强队的可能。


    假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩，得出每个队与另一个队对阵时取胜的概率表:


    甲  乙  丙  丁   
甲   -  0.1 0.3 0.5
乙 0.9  -   0.7 0.4 
丙 0.7  0.3 -   0.2
丁 0.5  0.6 0.8 -


    数据含义：甲对乙的取胜概率为0.1，丙对乙的胜率为0.3，...


    现在要举行一次锦标赛。双方抽签，分两个组比，获胜的两个队再争夺冠军。（参见【1.jpg】）


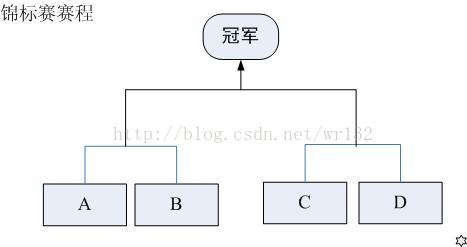
    请你进行10万次模拟，计算出甲队夺冠的概率。




    注意：

    请仔细调试！您的程序只有能运行出正确结果的时候才有机会得分！

开始不知道这题想表达什么，忽然想起了以前的一道通过随机函数求π的估值的java题，估计这道题也是需要使用随机函数的，而且还要进行十万次模拟，简直蛋疼，其实这种级别的数学题在我们学概率的时候就应该能做出来，而且能算出准确的平均概率，首先，找甲的第一个对手，可能是乙丙丁，然后再找第二个对手，比如，甲的第一个对手是乙，那丙和丁就是对手，再假设甲的第二个对手是丙，那丙必须战胜丁，并且甲两次都取得胜利，那么本次胜利的概率就是0.1*0.2*0.3，分别是甲战胜乙的概率，丙战胜丁的概率和甲战胜丙的概率，按照甲的第一个对手进行分类，有三种，然后将所有的情况的概率相加，除以3，就可以得到准确的数值。

#include<iostream>
using namespace std;
double rate[4][4]={{0,0.1,0.3,0.5},{0.9,0,0.7,0.4},{0.7,0.3,0,0.2},{0.5,0.6,0.8,0}};int main()
{int i,j,k;double time,sum;time=0;sum=0;for(i=1;i<4;i++){for(j=1;j<4;j++){for(k=1;k<4;k++){if(j!=i&&k!=i&&j!=k){sum+=rate[0][i]*rate[j][k]*rate[0][j];}}}time++;}cout<<sum/time;return 0;
}