神经网络算法——反向传播 Back Propagation

本文主要是介绍神经网络算法——反向传播 Back Propagation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

---

前言

本文将从反向传播的本质、反向传播的原理、反向传播的案例三个方面，详细介绍反向传播（Back Propagation）。

反向传播

---

1、反向传播的本质

（1）前向传播（Forward Propagation）

前向传播是神经网络通过层级结构和参数，将输入数据逐步转换为预测结果的过程，实现输入与输出之间的复杂映射。

前向传播

• 输入层：

        输入层接收训练集中的样本数据。

        每个样本数据包含多个特征，这些特征被传递给输入层的神经元。

        通常，还会添加一个偏置单元来辅助计算。

• 隐藏层：

        隐藏层的每个神经元接收来自输入层神经元的信号。

        这些信号与对应的权重相乘后求和，并加上偏置。

        然后，通过激活函数（如sigmoid）处理这个求和结果，得到隐藏层的输出。

• 输出层：

        输出层从隐藏层接收信号，并进行类似的加权求和与偏置操作。

        根据问题的类型，输出层可以直接输出这些值（回归问题），或者通过激活函数（如softmax）转换为概率分布（分类问题）。

（2）反向传播（Back Propagation）

反向传播算法利用链式法则，通过从输出层向输入层逐层计算误差梯度，高效求解神经网络参数的偏导数，以实现网络参数的优化和损失函数的最小化。

反向传播

• 利用链式法则：

        反向传播算法基于微积分中的链式法则，通过逐层计算梯度来求解神经网络中参数的偏导数。

• 从输出层向输入层传播：

        算法从输出层开始，根据损失函数计算输出层的误差，然后将误差信息反向传播到隐藏层，逐层计算每个神经元的误差梯度。

• 计算权重和偏置的梯度：

        利用计算得到的误差梯度，可以进一步计算每个权重和偏置参数对于损失函数的梯度。

• 参数更新：

        根据计算得到的梯度信息，使用梯度下降或其他优化算法来更新网络中的权重和偏置参数，以最小化损失函数。

2、反向传播的原理

（1）链式法则（Chain Rule）

链式法则是微积分中的一个基本定理，用于计算复合函数的导数。如果一个函数是由多个函数复合而成，那么该复合函数的导数可以通过各个简单函数导数的乘积来计算。

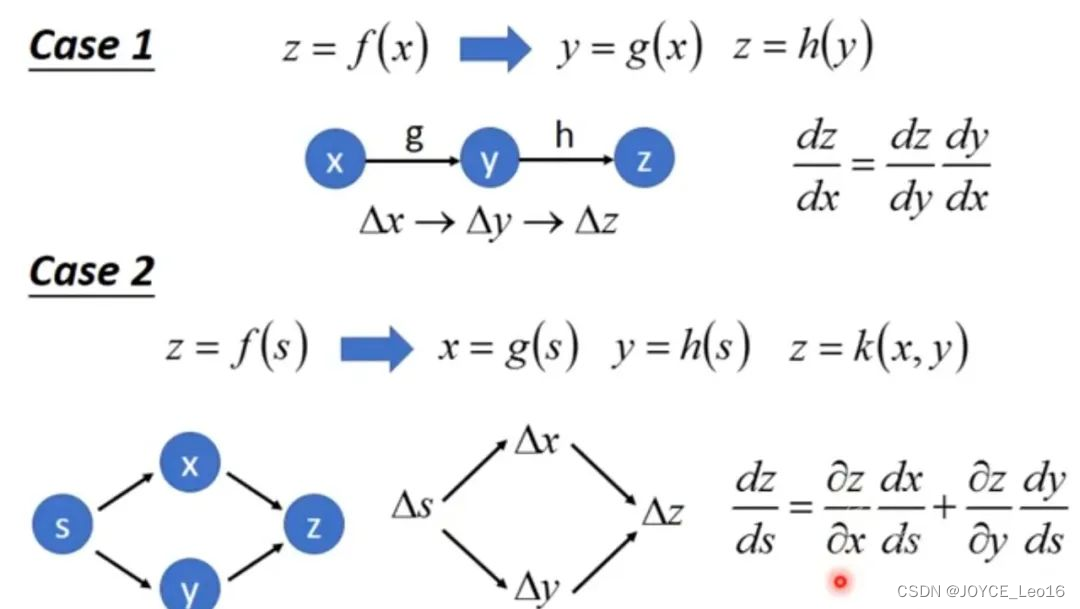
链式法则

• 简化梯度计算：

        在神经网络中，损失函数通常是一个复合函数，由多个层的输出和激活函数组合而成。链式法则允许我们将这个复杂的复合函数的梯度计算分解为一系列简单的局部梯度计算，从而简化了梯度计算的过程。

• 高效梯度计算：

        通过链式法则，我们可以从输出层开始，逐层向前计算每个参数的梯度，这种逐层计算的方式避免了重复计算，提高了梯度计算的效率。

• 支持多层网络结构：

        链式法则不仅适用于简单的两层神经网络，还可以扩展到具有任意多层结构的深度神经网络。这使得我们能够训练和优化更加复杂的模型。

（2）偏导数

偏导数是多元函数中对单一变量求导的结果，它在神经网络反向传播中用于量化损失函数随参数变化的敏感度，从而指导参数优化。

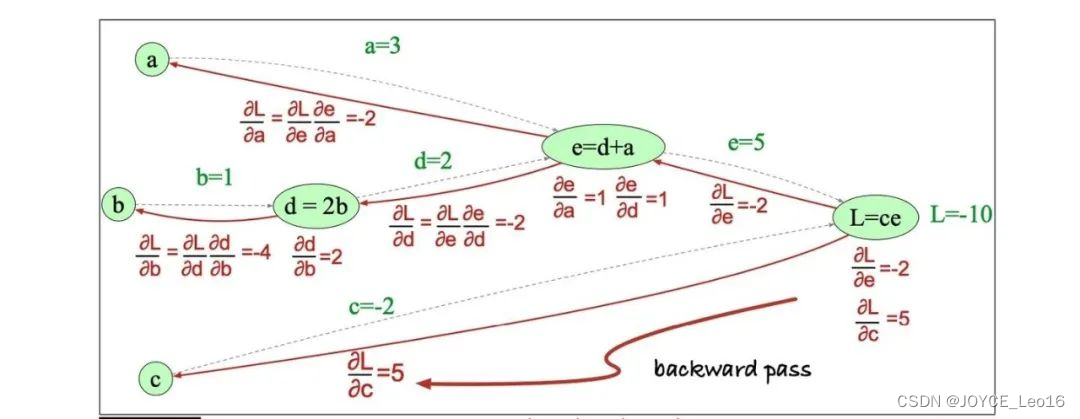
偏导数

• 偏导数的定义：

        偏导数是指在多元函数中，对其中一个变量求导，而将其余变量视为常数的导数。

        在神经网络中，偏导数用于量化损失函数相对于模型参数（如权重和偏置）的变化率。

• 反向传播的目标：

        反向传播的目标是计算损失函数相对于每个参数的偏导数，以便使用优化算法（如梯度下降）来更新参数。

        这些偏导数构成了梯度，指导了参数更新的方向和幅度。

• 计算过程：

        输出层偏导数：首先计算损失函数相对于输出层神经元输出的偏导数。这通常直接依赖于所选的损失函数。

        隐藏层偏导数：使用链式法则，将输出层的偏导数向后传播到隐藏层。对于隐藏层中的每个神经元，计算其输出相对于下一层神经元输入的偏导数，并与下一层传回的偏导数相乘，累积得到该神经元对损失函数的总偏导数。

        参数偏导数：在计算了输出层和隐藏层的偏导数之后，我们需要进一步计算损失函数相对于网络参数的偏导数，即权重和偏置的偏导数。

3、反向传播的案例：简单神经网络

（1）网络结构

• 假设我们有一个简单的两层神经网络，结构如下：

        输入层：2个神经元（输入特征 x1 和 x2）

        隐藏层：2个神经元（带有激活函数 sigmoid）

        输出层：1个神经元（带有激活函数 sigmoid）

• 网络的权重和偏置如下（这些值是随机初始化的，实际情况中会使用随机初始化）：

        输入层到隐藏层的权重矩阵 W1：[0.5, 0.3], [0.2, 0.4]

        隐藏层到输出层的权重向量 W2：[0.6, 0.7]

        隐藏层的偏置向量 b1：[0.1, 0.2]

        输出层的偏置 b2：0.3

（2）前向传播

• 给定输入 [0.5, 0.3]，进行前向传播：

        隐藏层输入：[0.5*0.5 + 0.3*0.2 + 0.1, 0.5*0.3 + 0.3*0.4 + 0.2] = [0.31, 0.29]

        隐藏层输出（经过 sigmoid 激活函数）：[sigmoid(0.31), sigmoid(0.29)]  [0.57, 0.57]

        输出层输入：0.6*0.57 + 0.7*0.57 + 0.3 = 0.71

        输出层输出（预测值，经过sigmoid激活函数）：sigmoid(0.71)  0.67

（3）损失计算

• 假设真实标签是 0.8，使用均方误差（MSE）计算损失：

        损失 = 

（4）反向传播

计算损失函数相对于网络参数的偏导数，并从输出层开始反向传播误差。

• 输出层偏导数：

        损失函数对输出层输入的偏导数 ：2 * (0.67 - 0.8) * sigmoid_derivative(0.71)  -0.05

Sigmoid函数的导数：sigmoid(x) * (1 - sigmoid(x))

• 隐藏层偏导数：

        损失函数对隐藏层每个神经元输出的偏导数：[δ2 * 0.6 * sigmoid_derivative(0.31), δ2 * 0.7 * sigmoid_derivative(0.29)]

        计算后得到 δ1 ≈ [-0.01, -0.01]（这里简化了计算，实际值可能有所不同）

• 参数偏导数：

        对于权重 W2：[δ2 * 隐藏层输出1，δ2 * 隐藏层输出2] = [-0.03, -0.04]

        对于偏置 b2：δ2 = -0.05

        对于权重 W1 和 偏置 b1，需要更复杂的计算，因为它们影响到隐藏层的输出，进而影响到输出层的输入和最终的损失。这些偏导数依赖于 δ1 和输入层的值。

（5）参数更新

• 使用梯度下降更新参数（学习率设为 0.1）：

        更新 W2：w2 - 学习率 * 参数偏导数

        更新 b2：b2 - 学习率 * 参数偏导数

        同样地更新 W1 和 b1

（6）迭代

• 重复步骤 2-5，直到网络收敛或达到预设的迭代次数。

参考：架构师带你玩转AI

这篇关于神经网络算法——反向传播 Back Propagation的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---