ReDet:A Rotation-equivariant Detector for Aerial Object Detection

2024-03-05 17:58
文章标签 object detection aerial rotation equivariant detector redet

本文主要是介绍ReDet:A Rotation-equivariant Detector for Aerial Object Detection，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

ReDet:A Rotation-equivariant Detector for Aerial Object Detection

image-20210727140437703

文章目录

        • ReDet:A Rotation-equivariant Detector for Aerial Object Detection
          • 参考
          • Introduction
          • Related Works
          • Preliminaries
            • Rotation-equivariant Networks
            • Rotation-invariant Features
          • Rotation-equivariant Detector
            • Rotation-equivariant Backbone：旋转同变Backbone
            • Rotation-invariant RoI Align：旋转不变RoI Align
          • Experiments and Analysis

参考
  • 笔记：1、论文笔记：ReDet: A Rotation-equivariant Detector for Aerial Object Detection
  • 翻译：2、ReDet A Rotation-equivariant Detector for Aerial Object Detection 论文学习
  • 翻译：3、Learning roi transformer for oriented object detection in aerial images
  • 笔记：4、 [论文笔记]Arbitrary-Oriented Scene Text Detection via Rotation Proposals
  • 笔记：5、《RRPN：Arbitrary-Oriented Scene Text Detection via Rotation Proposals》论文笔记
  • 笔记：6、R3Det: Refined Single-Stage Detector with Feature Refinement for Rotating Object
  • 笔记：7、论文笔记：Group Equivariant Convolutional Networks
  • 原文：8、HEXACONV
  • 笔记：9、[论文理解]旋转等变向量场网络Rotation equivariant vector field networks
  • 笔记：10、Oriented Response Networks 论文解读
  • 笔记：11、有方向的CNN–Oriented Response Networks
  • 笔记：12、[论文理解]E(2)群等变可操控神经网络General E(2) - Equivariant Steerable CNNs
  • 笔记：13、[论文理解]为旋转等变CNN学习可操纵卷积核Learning Steerable Filters for Rotation Equivariant CNNs
  • 笔记：14、[论文理解]谐波网络：深度平移和旋转等变Harmonic Networks: Deep Translation and Rotation Equivariance
  • 视频：15、Harmonic Networks: Deep Translation and Rotation Equivariance
  • 笔记：16、ROI Pooling和ROI Align
  • 笔记：17、遥感检测——RoI Transformer（CVPR2019）
  • 笔记：18、RoIAlign/RoIPooling CUDA源码解读
Introduction
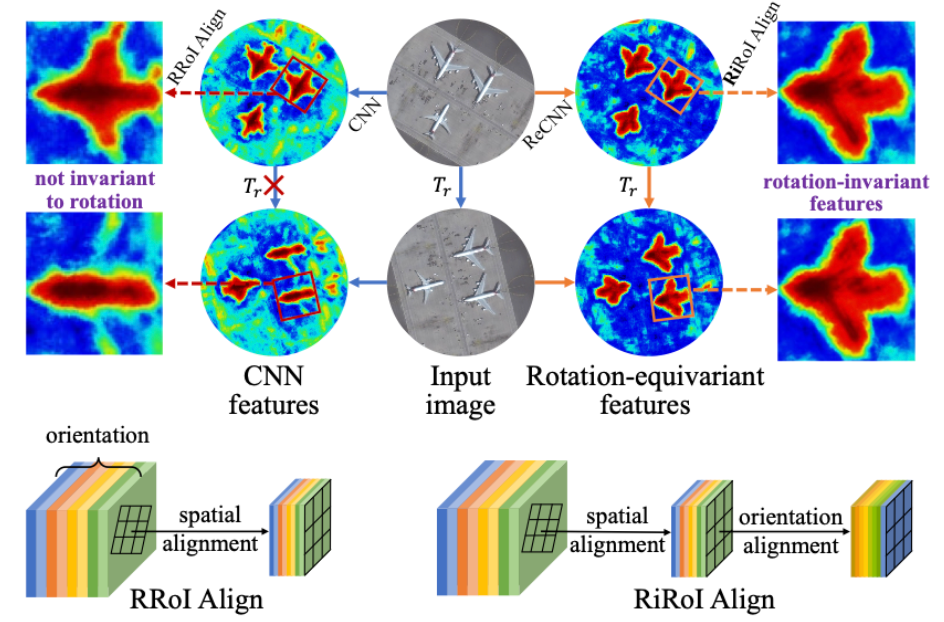
  • CNN特征不具有旋转不变性，上图中上半部分将Input旋转了一个角度，输入左图用普通CNN提取feature map得到的feature是不同的，而输入到右图中提取了旋转同变特征（ Rotation-equivariant features,ReCNN提取）
    • RoI-Align只能在空间维度上实现旋转不变性，ReDet提出了一种新的旋转不变性RoI（RiRoI）Align算法来提取空间维度和方向维度上的旋转不变性特征
      • 直接将普通RRoI旋转应用到旋转同变特征上并不能产生旋转不变特征，因为它只能旋转二维平面上的区域特征，即空间维度（可以理解为前两维），而方向通道仍然是错位的（channel）。为了提取完全旋转不变的特征，我们还需要根据RRoI的方向调整特征图的方向维数。
      • 具体的方式如上图的右下角所示，在原来RRoI的基础上，再加一次方向维度的调整，原文是说用的循环转换各个通道
        • by circularly switching orientation channels and feature interpolation
    • 因此，所谓rotation-invariant feature = rotation-equivariant backbone + Ri RoI
      • Ri RoI = RRoI + orientation alignment
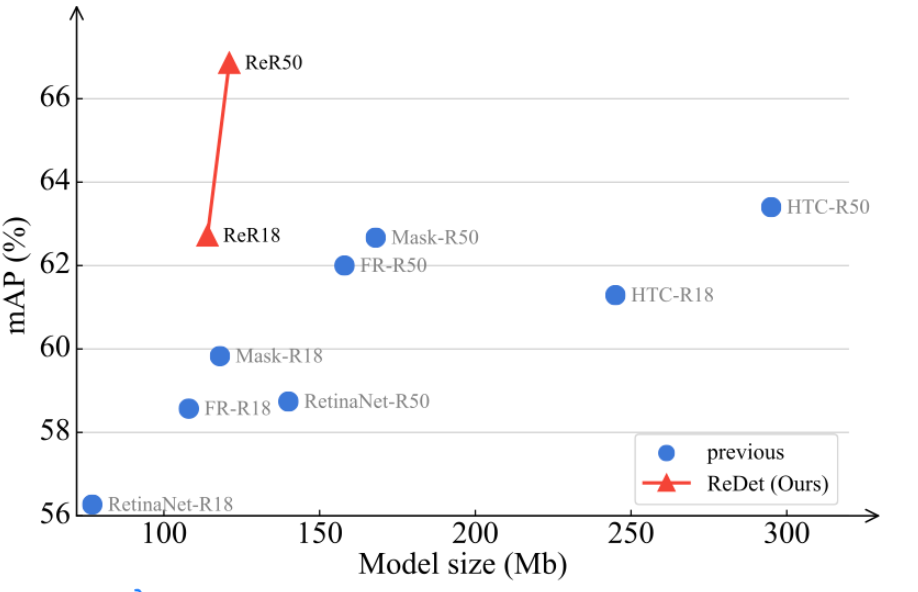
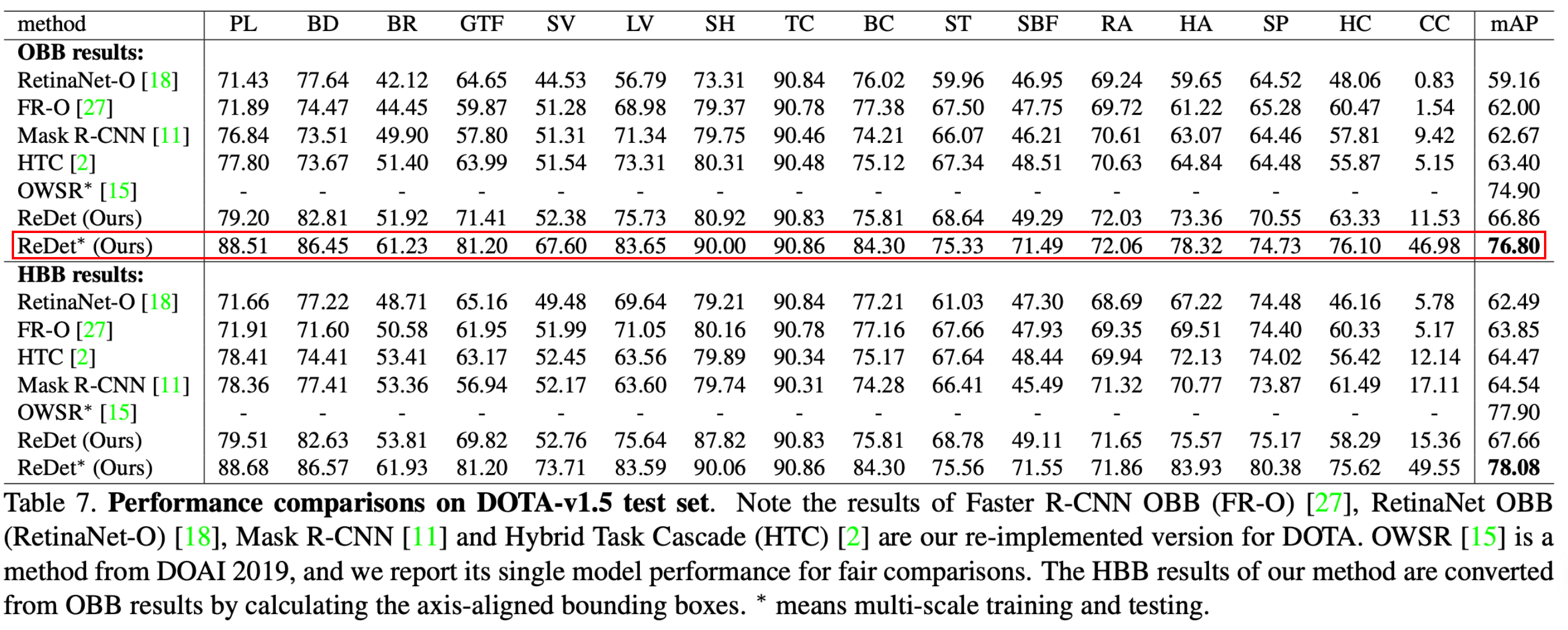
  • R18代表采用了ResNet18作为backbone，ReR50同理
    • ReR18在效果上几乎追平其他模型的R50版本，ReR50更是在参数量较少的前提下拥有最高的mAP
Related Works
  • HBB->OBB
  • Rotation-equivariant Networks，将下面的方法从分类任务中引入目标检测任务中去
    • 提出了群卷积，将4倍旋转同变纳入CNN
      • 参考：论文笔记：Group Equivariant Convolutional Networks
    • 将群卷积推广到六角格子上的6倍旋转同变
      • HEXACONV
    • 通过插值对滤波器进行再采样
      • 参考：[论文理解]旋转等变向量场网络Rotation equivariant vector field networks
      • 参考：Oriented Response Networks 论文解读
      • 参考：有方向的CNN–Oriented Response Networks
    • 使用谐波（harmonics）作为滤波器在连续域中产生equivariant feature（所谓滤波器就是多个卷积核的堆叠），根据代码实现，作者采用的是参考1，借用e2cnn的实现来重写backbone，
      • 参考：[论文理解]E(2)群等变可操控神经网络General E(2) - Equivariant Steerable CNNs
      • 参考：[论文理解]为旋转等变CNN学习可操纵卷积核Learning Steerable Filters for Rotation Equivariant CNNs
      • 参考：[论文理解]谐波网络：深度平移和旋转等变Harmonic Networks: Deep Translation and Rotation Equivariance
        • 视频：Harmonic Networks: Deep Translation and Rotation Equivariance
        • Regular CNN
        • hnet
  • Rotation-invariant Object Detection
    • 旋转不变的特征对于任意朝向的目标检测来说很重要。但是，CNN 对旋转变化进行建模的能力很差，也就是说需要更多的参数来编码朝向信息。STN 和 DCN 直接在网络中建模旋转角度，在朝向目标检测上广泛使用。Cheng 等人提出了一个旋转不变层，对目标函数施加了一个显式的正则约束。尽管上述方法能够取得旋转不变性的近似效果，但需要大量的参数和训练样本。此外，目标检测需要实例级的旋转不变特征。因此，一些方法将 RoI warping 扩展为 RRoI warping，比如 RoI Transformer 学习如何将 HRoIs 变换为 RRoIs，然后利用一个旋转的位置敏感的 RoI Align 操作来扭曲区域特征。但是正常的 CNN 不具备旋转同变性。所以，哪怕通过 RRoI Align，我们仍无法提取出旋转不变特征。和这些方法不同，本文方法通过旋转不变 RoI Align(RiRoI Align) 从旋转同变特征中提取旋转不变特征。作者在主干网络中加入了旋转同变网络，产生旋转同变特征，然后在空间维度和朝向维度，利用 RiRoI Align 从旋转同变特征中提取出旋转不变特征。
Preliminaries

  • 同变性就是说，如果我们对模型的输入做变换，我们应该可以预测该特征的变换结果。

    • 给定一个变换群 G 和函数 $\Phi： X\rightarrow Y $，同变性可以表示为：

    Φ [ T g X ( x ) ] = T g Y [ Φ ( x ) ] ∀ ( x , g ) ∈ ( X , G ) ( 1 ) \Phi[T^X_g(x)] = T^Y_g[\Phi(x)] \qquad ∀(x, g) ∈ (X, G) \qquad (1) Φ[TgX​(x)]=TgY​[Φ(x)]∀(x,g)∈(X,G)(1)

    • 其中 T g T_g Tg​表示在相应空间内的一组的操作。如果所有 T g X T_g^X TgX​和 T g Y T_g^Y TgY​的值是一样的，同变性就变成了不变性

    • 对于上面这段公式，个人理解是：

      • T g X T_g^X TgX​的意思应该是对X做 T g T_g Tg​变换，同理 T g Y T_g^Y TgY​的意思应该是对Y做 T g T_g Tg​变换，但是这两种变换不一定是相同的
      • 对于输入x，对其做变换得到 T g X ( x ) T_g^X(x) TgX​(x)然后再经过函数 Φ \Phi Φ得到 Φ ( T g X ( x ) ) \Phi(T_g^X(x)) Φ(TgX​(x))，即可理解为先对图片做变换再输入模型中去
      • 若先再经过函数 Φ \Phi Φ得到 Φ ( x ) \Phi(x) Φ(x)，再对其进行变换得到 T g Y ( Φ ( x ) ) T_g^Y(\Phi(x)) TgY​(Φ(x))，即可理解为把图片输入到模型中去，再对输出对结果做一定变换
      • 上述的两个变换不一定相同，但是当对于 T g X T_g^X TgX​变换总存在一个 T g Y T_g^Y TgY​变换使得(1)等式成立，则说模型具有同变性，当所有 T g X T_g^X TgX​和 T g Y T_g^Y TgY​的变换是一样的，则说明
      • 这里引入了群论，群有一个性质，如果两个群满足双射的条件，也即存在一个变换，可以让两个群的元素一一对应，那么就称这两个群是同构的（特指等距同构）。等距同构是指在度量空间之间保持距离关系的同构。在几何学中对应全等变换。

  • 以CNN的平移同变性为例(等式的左右两边的 T t T_t Tt​变换相同时，原文没说相同，因此用了同变性)：

    • 让 T t T_t Tt​表示平移分组( R 2 R^2 R2,+)的一个操作，将其应用在K维的特征图 f f f上：$Z^2 \rightarrow R^K $，平移不变性可以表示为：

    [ [ T t Z 2 f ] ∗ ϕ ] ( x ) = [ T t R K [ f ∗ ϕ ] ] ( x ) ( 2 ) [[T_t^{Z^2} f]*\phi](x) = [T_t^{R^K}[f*\phi]] (x) \qquad (2) [[TtZ2​f]∗ϕ](x)=[TtRK​[f∗ϕ]](x)(2)

    • 对于上述公式:

      • x ∈ ( R 2 , + ) x\in (R^2,+) x∈(R2,+)， ∗ * ∗表示卷积操作， ϕ \phi ϕ表示卷积核， f ∗ ϕ f*\phi f∗ϕ则表示对输入x得到的特征图 f f f进行卷积，而 T t f T_t f Tt​f则表示先对特征图进行平移变换
      • 于是先平移后卷积得到的结果可以通过先卷积然后进行（不一定相同的）平移操作得到，此为CNN的平移同变性
      • 当然对于CNN来说，一般 T t Z 2 T_t^{Z^2} TtZ2​= T t R K T_t^{R^K} TtRK​，因此具有平移不变性

  • 所谓旋转同变性，可以参考平移同变性：

    • 最近提出的一些方法将 CNN 扩展为更大的分组，实现平移不变和旋转不变(e2cnn)，以 H表示旋转分组，如循环分组 C N C_N CN​ 包含多个离散的旋转角度，角度为 $\frac{2\pi}{N} $的倍数,我们可以定义分组G为平移分组 ( R 2 R^2 R2 , + ) 和旋转分组H的间接乘积，即 G ≅ ( R 2 , + ) ⋊ H G \cong (R^2,+) \rtimes H G≅(R2,+)⋊H。在等式2中，将 x ∈ ( R 2 , + ) x\in (R^2,+) x∈(R2,+)替换成 g ∈ G g \in G g∈G，旋转同变性卷积可以定义为：

    [ [ T g Z 2 f ] ∗ ϕ ] ( g ) = [ T g R K [ f ∗ ϕ ] ] ( g ) ( 3 ) [[T_g^{Z^2} f]*\phi](g) = [T_g^{R^K}[f*\phi]] (g) \qquad (3) [[TgZ2​f]∗ϕ](g)=[TgRK​[f∗ϕ]](g)(3)

Rotation-equivariant Networks
  • 正常的 CNN 由一系列卷积层组成，具有平移权重共享的性质。类似地，旋转同变性网络也由一组旋转同变层组成，权重共享的程度更高，即平移和旋转权重共享。（将(3)的结论推广到所有层），以 Φ = { L i ∣ i ∈ { 1 , 2.... , M } } \Phi = \{ L_i|i \in \{ 1,2....,M\}\} Φ={Li​∣i∈{1,2....,M}}表示分组G，具有M个旋转同变层的网络，对某一层 L i ∈ Φ L_i \in \Phi Li​∈Φ,旋转变换 T r T_r Tr​可以通过该层保留下来：

L i [ T r Z 2 ( g ) ] = T r R K [ L i ( g ) ] g ∈ G ( 4 ) L_i[T_r^{Z^2}(g)] = T_r^{R^K}[L_i(g)] \qquad g \in G \qquad (4) Li​[TrZ2​(g)]=TrRK​[Li​(g)]g∈G(4)

  • 那么推广到全部忘了，如果对输入I使用 T r T_r Tr​,他会被每一层旋转同变卷积保留下来，进而被整个网络保留下来，于是就可以得到旋转同变的CNN了，如下所示：

[ ∏ i = 1 M L i ] ( T r Z 2 I ) = T r R K [ ∏ i = 1 M L i ] ( I ) ( 5 ) [\prod_{i=1}^ML_i](T_r^{Z^2}I) = T_r^{R^K}[\prod_{i=1}^ML_i](I) \qquad (5) [i=1∏M​Li​](TrZ2​I)=TrRK​[i=1∏M​Li​](I)(5)

Rotation-invariant Features

  • 对于输入做任意的旋转变换 T r T_r Tr​ ，如果输出保持不变，我们就说这个输出特征是旋转不变的。旋转不变特征可以分为3个层级：图像层级，实例层级和像素层级。这里我们主要关注实例层级的选择不变特征，对于目标检测任务来说更加适合。

  • （ROI部分）：对$ I_R\in I ， ， ， f_R\in f , 分 别 表 示 图 像 ,分别表示图像 ,分别表示图像I 的 R o I 和 特 征 图 的 RoI 和特征图 的RoI和特征图f 的 R o I , 的 RoI, 的RoI,f=\Phi(I) 。 假 设 。假设 。假设I_R 是 一 个 H o I ( x , y , w , h ) ， 对 朝 向 表 示 不 变 ， 是一个HoI(x,y,w,h)，对朝向表示不变， 是一个HoI(x,y,w,h)，对朝向表示不变，T_r 表 示 旋 转 操 作 ， 则 表示旋转操作，则 表示旋转操作，则T_rI_R 则 是 一 个 关 于 朝 向 则是一个关于朝向 则是一个关于朝向\theta 对 R R o I ( x , y , w , h , 对RRoI(x,y,w,h, 对RRoI(x,y,w,h,\theta$),那么可以得到和(5)类似的旋转同变的式子

Φ ( T r I R ) = T r Φ ( I R ) ( 6 ) \Phi(T_rI_R)=T_r\Phi(I_R) \qquad (6) Φ(Tr​IR​)=Tr​Φ(IR​)(6)

  • 我们如果将图像 I I I的HRoI（ I R I_R IR​）看作图像 I I I的RRoI( T r Z 2 I R T_r^{Z^2}I_R TrZ2​IR​)的旋转不变特征，那么 Φ ( I R ) \Phi(I_R) Φ(IR​)可以当作 Φ ( T r I R ) \Phi(T_rI_R) Φ(Tr​IR​)在对应特征空间的旋转不变特征(可由(6)式得到)。

    • 原文的意思我的理解是：原来backbone部分输出的是旋转同变特征，我们需要在RoI这里将其变为旋转不变特征，要使同变转化为不变，则等式左右两边的转化操作需要一样，也就是做另一侧的反操作( T r T_r Tr​通常就是朝向 θ \theta θ的一个函数： T r = T ( θ ) T_r=T(\theta) Tr​=T(θ))

    Φ ( I R ) = ( T r ) ′ Φ ( T r ) ( 7 ) \Phi(I_R) = (T_r)^{'} \Phi(T_r) \qquad (7) Φ(IR​)=(Tr​)′Φ(Tr​)(7)

Rotation-equivariant Detector

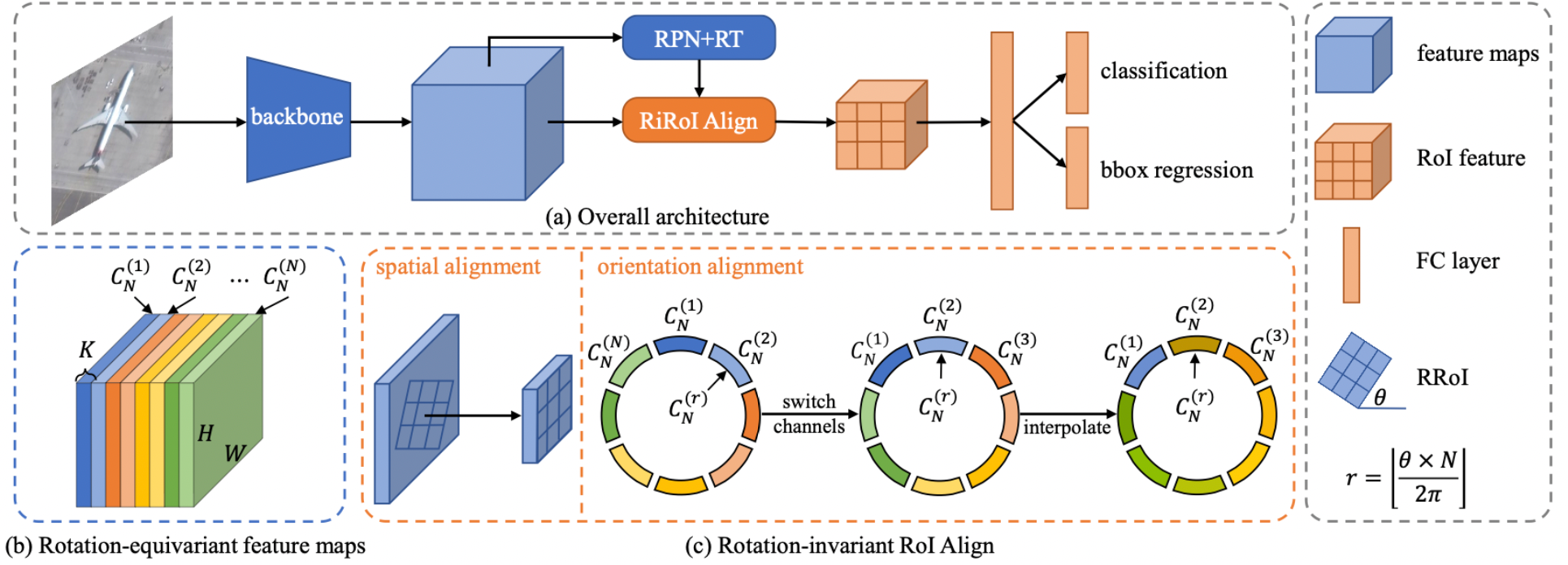
  • image-20210729150019787

    • 从上图可以看到ReDet采用了Faster RCNN的架构，其创新点由(b)©两图所示，
Rotation-equivariant Backbone：旋转同变Backbone
  • 这个由上面的理论得到，想要得到旋转同变特征，则需要得到旋转同变网络（Rotation-equivariant Networks），在实现上，作者将带有FPN的ResNet重写，使用e2cnn.nn替代torch.nn得到具有旋转同变的backbone——ReResNet，通过这个网络，可以得到旋转同变特征图。
  • 它有如下特点
    • (a) 更高度的权重共享。
    • (b)丰富的朝向信息。
    • © 模型体积更小。
Rotation-invariant RoI Align：旋转不变RoI Align

  • 其任务就是将旋转同变feature map转化后得到旋转不变的feature map（实例级），所谓旋转不变，就是无论输入如何改变（旋转），输出总是不变

  • 常见的 RRoI warping 只能在空间维度对齐特征，而没有对齐朝向维度。

    • 如上图 ©所示RiRoI Align 包含2个部分：(1)空间对齐。 (2) 朝向对齐。对于输出区域特征 f ^ R \hat f_R f^​R​,朝向对齐表示为：

    • f ^ R = I n t ( S C ( f R , r ) , θ ) , r = └ θ ∗ N 2 π ┘ ( 8 ) \hat f_R = Int(SC(f_R,r),\theta),\qquad r=\llcorner \frac{\theta*N}{2\pi} \lrcorner \qquad (8) f^​R​=Int(SC(fR​,r),θ),r=└2πθ∗N​┘(8)

    • 其中SC,Int分别表示切换通道和特征插值操作。

    • 对于输出区域特征$ f_R , 首 先 计 算 出 一 个 索 引 值 ,首先计算出一个索引值 ,首先计算出一个索引值r ， 然 后 循 环 地 切 换 朝 向 通 道 ， 确 保 ，然后循环地切换朝向通道，确保 ，然后循环地切换朝向通道，确保C_N^{®} 是 第 一 个 朝 向 通 道 。 但 是 因 为 旋 转 同 变 性 只 在 里 塞 的 分 组 是第一个朝向通道。但是因为旋转同变性只在里塞的分组 是第一个朝向通道。但是因为旋转同变性只在里塞的分组C_N 中 得 到 ， 如 果 中得到，如果 中得到，如果\theta \notin C_N 我 们 需 要 对 特 征 做 插 值 ， 我 们 用 最 近 的 我们需要对特征做插值，我们用最近的 我们需要对特征做插值，我们用最近的l 朝 向 特 征 做 插 值 ， 如 , 朝向特征做插值，如, 朝向特征做插值，如,l=2 的 第 的第 的第i$个朝向通道的输出特征可以表示为：

    • f ^ R ( i ) = ( 1 − α ) f R ( i ) + α f R ( i + 1 ) ( 9 ) \hat f_R^{(i)} = (1- \alpha)f_R^{(i)} +\alpha f_R^{(i+1)} \qquad (9) f^​R(i)​=(1−α)fR(i)​+αfR(i+1)​(9)

    • 其中 α = θ ∗ N 2 π \alpha = \frac{ \theta * N}{2 \pi} α=2πθ∗N​ 表示一维插值的距离因子，同时 i ∈ [ 1 , N ] i \in [1,N] i∈[1,N]，可以使用mod函数实现

  • 在实现中，作者先对再进行RRoI（参考RoI Transformer中的方法）,然后channel进行旋转（用rotate比较合适）与插值

    • 18、RoIAlign/RoIPooling CUDA源码解读

    • //文件位于：ReDet/mmdet/ops/riroi_align/src/riroi_align_kernel.cu/RiROIAlignForward
// 这里是旋转的代码
//nOrientation表示结构图中的N，代表把特征图分成N块
// o在这里表示分出来的块的编号
int o = (index / pooled_width / pooled_height) % nOrientation;// TODO
// find aligned index
// 相当于图中r= [\theta * N / 2*PI]
scalar_t ind_float = theta * nOrientation / (2 * PI);
int ind =  floor(ind_float);
scalar_t l_var = ind_float - (scalar_t)ind;
scalar_t r_var = 1.0 - l_var;// correct start channel
// 开始通道编号
ind = (ind + nOrientation) % nOrientation;
// rotated channel
// 旋转通道
int ind_rot = (o - ind + nOrientation) % nOrientation;
int ind_rot_plus = (ind_rot + 1 + nOrientation) % nOrientation; const scalar_t* offset_bottom_data =bottom_data + (roi_batch_ind * channels * nOrientation + c * nOrientation + ind_rot) * height * width;const scalar_t* offset_bottom_data_plus =bottom_data + (roi_batch_ind * channels * nOrientation + c * nOrientation + ind_rot_plus) * height * width;//...//
// 双线性插值
scalar_t val = bilinear_interpolate<scalar_t>(offset_bottom_data, height, width, y, x);
scalar_t val_plus = bilinear_interpolate<scalar_t>(offset_bottom_data_plus, height, width, y, x);
output_val += r_var * val + l_var * val_plus;
}
Experiments and Analysis
  • image-20210730004421241

这篇关于ReDet:A Rotation-equivariant Detector for Aerial Object Detection的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/777348。

相关文章

【Python报错已解决】AttributeError: ‘list‘ object has no attribute ‘text‘

【Python报错已解决】AttributeError: ‘list‘ object has no attribute ‘text‘

🎬 鸽芷咕：个人主页  🔥 个人专栏: 《C++干货基地》《粉丝福利》 ⛺️生活的理想，就是为了理想的生活! 文章目录 前言一、问题描述1.1 报错示例1.2 报错分析1.3 解决思路 二、解决方法2.1 方法一：检查属性名2.2 步骤二：访问列表元素的属性 三、其他解决方法四、总结 前言 在Python编程中，属性错误（At
阅读更多...
时间序列|change point detection

时间序列|change point detection

change point detection 被称为变点检测，其基本定义是在一个序列或过程中，当某个统计特性（分布类型、分布参数）在某时间点受系统性因素而非偶然因素影响发生变化，我们就称该时间点为变点。变点识别即利用统计量或统计方法或机器学习方法将该变点位置估计出来。 Change Point Detection的类型 online 指连续观察某一随机过程，监测到变点时停止检验，不运用到
阅读更多...
error while loading shared libraries: libnuma.so.1: cannot open shared object file:

error while loading shared libraries: libnuma.so.1: cannot open shared object file:

腾讯云CentOS，安装Mysql时: 1.yum remove libnuma.so.1 2.yum install numactl.x86_64
阅读更多...
java基础总结12-面向对象8（Object类）

java基础总结12-面向对象8（Object类）

1 Object类介绍 Object类在JAVA里面是一个比较特殊的类，JAVA只支持单继承，子类只能从一个父类来继承，如果父类又是从另外一个父类继承过来，那他也只能有一个父类，父类再有父类，那也只能有一个，JAVA为了组织这个类组织得比较方便，它提供了一个最根上的类，相当于所有的类都是从这个类继承，这个类就叫Object。所以Object类是所有JAVA类的根基类，是所有JAVA类的老祖宗
阅读更多...
MACS bdgdiff: Differential peak detection based on paired four bedGraph files.

MACS bdgdiff: Differential peak detection based on paired four bedGraph files.

参考原文地址：[http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html](http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html) 文章目录 一、MACS bdgdiff 简介DESCRIPTION 二、用法
阅读更多...
王立平--Object-c

王立平--Object-c

object-c通常写作objective-c或者obj-c，是根据C语言所衍生出来的语言，继承了C语言的特性，是扩充C的面向对象编程语言。它主要使用于MacOSX和GNUstep这两个使用OpenStep标准的系统，而在NeXTSTEP和OpenStep中它更是基本语言。Objective-C可以在gcc运作的系统写和编译，因为gcc含Objective-C的编译器。在MA
阅读更多...
Learning Memory-guided Normality for Anomaly Detection——学习记忆引导的常态异常检测

Learning Memory-guided Normality for Anomaly Detection——学习记忆引导的常态异常检测

又是一篇在自编码器框架中研究使用记忆模块的论文，可以看做19年的iccv的论文的衍生，在我的博客中对19年iccv这篇论文也做了简单介绍。韩国人写的，应该是吧，这名字听起来就像。 摘要abstract 我们解决异常检测的问题，即检测视频序列中的异常事件。基于卷积神经网络的异常检测方法通常利用代理任务(如重建输入视频帧)来学习描述正常情况的模型，而在训练时看不到异常样本，并在测试时使用重建误
阅读更多...
REMEMBERING HISTORY WITH CONVOLUTIONAL LSTM FOR ANOMALY DETECTION——利用卷积LSTM记忆历史进行异常检测

REMEMBERING HISTORY WITH CONVOLUTIONAL LSTM FOR ANOMALY DETECTION——利用卷积LSTM记忆历史进行异常检测

上海科技大学的文章，上海科技大学有个组一直在做这方面的工作，好文章挺多的还有数据集。 ABSTRACT 本文解决了视频中的异常检测问题，由于异常是无界的，所以异常检测是一项极具挑战性的任务。我们通过利用卷积神经网络(CNN或ConvNet)对每一帧进行外观编码，并利用卷积长期记忆(ConvLSTM)来记忆与运动信息相对应的所有过去的帧来完成这项任务。然后将ConvNet和ConvLSTM与
阅读更多...
COD论文笔记 ECCV2024 Just a Hint: Point-Supervised Camouflaged Object Detection

COD论文笔记 ECCV2024 Just a Hint: Point-Supervised Camouflaged Object Detection

这篇论文的主要动机、现有方法的不足、拟解决的问题、主要贡献和创新点： 1. 动机 伪装物体检测（Camouflaged Object Detection, COD）旨在检测隐藏在环境中的伪装物体，这是一个具有挑战性的任务。由于伪装物体与背景的细微差别和模糊的边界，手动标注像素级的物体非常耗时，例如每张图片可能需要 60 分钟来标注。因此，作者希望通过减少标注负担，提出了一种仅依赖“点标注”的弱
阅读更多...
COD论文笔记 Adaptive Guidance Learning for Camouflaged Object Detection

COD论文笔记 Adaptive Guidance Learning for Camouflaged Object Detection

论文的主要动机、现有方法的不足、拟解决的问题、主要贡献和创新点如下： 动机： 论文的核心动机是解决伪装目标检测（COD）中的挑战性任务。伪装目标检测旨在识别和分割那些在视觉上与周围环境高度相似的目标，这对于计算机视觉来说是非常困难的任务。尽管深度学习方法在该领域取得了一定进展，但现有方法仍面临有效分离目标和背景的难题，尤其是在伪装目标与背景特征高度相似的情况下。 现有方法的不足之处： 过于
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2