本文主要是介绍局部自适应时空图神经网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

KDD2023
摘要
时空图模型是抽象和建模时空依赖关系的主流。在这项工作中,我们提出了以下问题:我们是否以及在多大程度上可以局部化时空图模型?我们将研究范围限制在自适应时空图神经网络(astgnn),这是最先进的模型架构。我们的定位方法涉及到空间图邻接矩阵的稀疏化。为此,我们提出了自适应图稀疏化(AGS),这是一种图稀疏化算法,它成功地使astgnn的本地化达到了极限(完全本地化)。我们将AGS应用于两种不同的ASTGNN架构和9个时空数据集。
有趣的是,我们观察到astgnn中的空间图可以在不降低测试精度的情况下稀疏化超过99.5%。此外,即使astgnn完全局部化,变得无图形化和纯时间化,我们也没有记录到大多数测试数据集的准确性下降,在其余数据集中只观察到轻微的准确性下降。然而,当部分或完全定位的astgnn在相同的数据上重新初始化和重新训练时,准确性会出现相当大的持续下降。
基于这些观察,我们认为(i)在测试数据中,空间依赖关系提供的信息主要包含在时间依赖关系提供的信息中,因此在推理中基本上可以忽略;(ii)尽管空间依赖关系提供了冗余信息,但它对于astgnn的有效训练至关重要,因此在训练过程中不能忽视。此外,astgnn的本地化有可能减少大规模时空数据所需的繁重计算开销,并进一步实现astgnn的分布式部署。
1 介绍
越来越多的现代智能应用[3,6,24]依赖于时空数据,即跨越空间和时间收集的数据。时空数据通常包含空间和时间依赖关系,即在特定位置的当前测量与同一位置和其他位置的历史状态具有因果依赖关系。学习这些时空依赖关系通常是时空数据挖掘的本质,在时空推理中起着至关重要的作用[1]。
时空图模型可以有效地表示时空数据,时空图模型可以描述非欧几里得域中对象之间的复杂关系和相互依赖关系[2,11,12,19,21,24,24,26,28]。我们特别感兴趣的是自适应时空图神经网络(astgnn),这是一类流行的时空图模型,在涉及时空数据的应用中表现出色,如交通预测、区块链价格预测和生物监测预测[3,6 - 8,24,25]。
在这项工作中,我们提出了以下问题:我们是否以及在多大程度上可以局部化时空图模型?我们的研究仅限于astgnn,因为它们代表了最先进的时空图模型架构。astgnn通常使用自适应图卷积层对空间依赖性进行建模。空间依赖关系是通过学习图邻接矩阵来捕获的。因此,ASTGNN的定位是通过邻接矩阵的稀疏化来实现的,这也可以理解为空间图中的剪枝边。请注意,ASTGNN的局部化是指仅对捕获空间依赖关系的邻接矩阵进行稀疏化。至关重要的是,不要与稀疏化其他权重矩阵相混淆,例如在时间模块中使用的权重矩阵,通常在具有预定义图架构的GNN稀疏化中看到[5,16,27,29]。
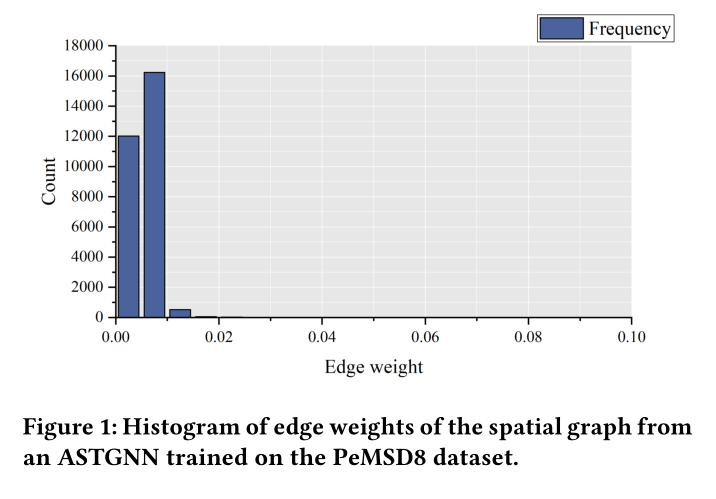
图1显示了一个初步的线索,表明ASTGNN的定位是可行的,甚至可能达到极端的程度。这里我们展示了在PeMSD8数据集上训练的ASTGNN在空间图邻接矩阵中的元素分布[4]。很明显,空间图中大多数边的权值接近于零。
我们对时空图模型的本地化感兴趣,原因如下:
•对数据中的时空依赖关系有更深的理解。虽然人们普遍认为空间和时间依赖关系对推理都是至关重要的,但尚不清楚这些依赖关系提供的信息是否重叠,以及在多大程度上重叠。如果定位导致边际精度下降,那么空间依赖项提供的信息已经在很大程度上包含在时间依赖项所包含的信息中,因此不需要进行推理。
•资源高效的ASTGNN设计。astgnn是出了名的计算量大,因为空间图的大小与顶点的数量呈二次增长,从而限制了它们在大规模数据和应用程序中的使用。astgnn的本地化可以显著减少这些时空图模型的资源需求,并实现新的时空应用。
•分布式部署的时空图模型。在许多情况下,构建时空图模型的数据是通过分布式传感系统(如传感器网络)收集的。然而,使用这些模型对每个顶点进行预测需要其他顶点的历史,因此涉及传感器节点之间的数据交换。时空图模型的本地化可以使单个传感器节点在不相互通信的情况下自主进行预测,从而节省了带宽并保护了分布式系统的隐私。
我们通过自适应图稀疏化(AGS)来探索astgnn的定位,AGS是一种致力于astgnn中邻接矩阵稀疏化的新算法。AGS的核心是掩模矩阵正则化的可微近似,它允许反向传播通过正则化器,从而在训练时实现渐进稀疏化。
我们将AGS应用于两个具有代表性的ASTGNN架构和九个不同的时空数据集。实验结果令人惊讶。(i)空间邻接矩阵可以被稀疏到99.5%以上,而不会降低所有数据集的测试精度。(ii)即使是完全局部化的astgnn,它有效地退化为纯时间模型,仍然可以提供不错的测试精度(在大多数测试数据集上没有退化,而在其余数据集上只有轻微的精度下降)。(iii)当我们重新初始化局部astgnn的权重并在时空数据集上重新训练它们时,我们无法恢复相同的推理精度。图2总结了我们的实验和观察结果。
我们的实证研究包含两个假设。(i)在经过测试的时空数据集中,空间依赖项提供的信息主要包含在时间依赖项提供的信息中。因此,可以安全地忽略空间依赖关系来进行推理,而不会有明显的准确性损失。虽然空间和时间依赖关系中包含的信息重叠,但这种重叠提供了适当训练时空图模型所必需的重要冗余。因此,在训练过程中不能忽略空间依赖性。
我们的主要贡献总结如下:
•据我们所知,这是第一个关于时空图模型本地化的研究。我们惊讶地发现,在推理过程中,空间依赖关系可以在很大程度上被忽略,而不会失去准确性。在常见的时空数据集和代表性的ASTGNN架构上进行的大量实验表明,只需要少量的边缘(在所有测试数据集上小于0.5%)就可以保持推理精度。更令人惊讶的是,当空间依赖关系被完全忽略时,即,astgnn被完全定位,它们仍然可以保持不错的推理精度(大多数测试数据集没有恶化,其余数据集略有下降)。
•通过进一步的研究,我们提出了这样的假设:尽管空间依赖关系在推理过程中可以被忽略,但它们可以极大地提高训练效率。观察结果支持了这一点,如果我们重新初始化稀疏化的astgnn中的所有参数并用相同的数据重新训练它们,重新训练的网络产生相当大且持续较差的准确性。
•为了实现astgnn的本地化,我们提出了自适应图稀疏化(AGS),这是一种专门用于astgnn的新型图稀疏化算法。AGS的核心是掩模矩阵正则化的可微近似,它允许反向传播通过正则化器,从而在训练时实现渐进稀疏化。
2相关工作
我们的工作与以下研究方向有关。
2.1时空图神经网络
时空图神经网络(stgnn)能够学习随时间变化的空间不规则信号的隐藏模式,在时空数据分析中发挥着至关重要的作用[24]。这些模型通常结合了图卷积网络和递归神经网络。例如,图卷积循环网络(Graph Convolutional Recurrent Network, GCRN)[21]将LSTM与ChebNet相结合。
扩散卷积递归神经网络[19]将提出的扩散图卷积层以编码器-解码器的方式整合到GRU中,进行多步预测。或者,基于cnn的模型可以以非递归的方式表示时空数据中的时间关系。例如,CGCN[28]将1D卷积层与GCN层相结合。STGCN[26]使用1D卷积层和PGC (Partition Graph Convolution)层构成了一个基于骨架的动作识别的时空模型。最近提出的ASTGCN[11]、STG2Seq[2]和LSGCN[12]进一步利用注意力机制对动态空间依赖关系和时间依赖关系进行建模。此外,也有研究者考虑到STGNN的分布外泛化问题,提出了基于超网络的域泛化框架来解决这一问题[10]。然而,这些模型采用了预定义的图形结构,这可能不能反映完整的空间依赖性。
为了捕捉时空数据图结构中的动态,利用自适应时空图神经网络(astgnn)是一个新兴的趋势。Graph WaveNet[25]提出了一种AGCN层,在没有预定义图的情况下学习归一化自适应邻接矩阵。ASTGAT引入了一种网络生成器模型,该模型使用GumbelSoftmax技术生成自适应离散图[15]。网络生成器可以自适应地从数据中推断出隐藏的相关性。AGCRN[3]设计了一种节点自适应参数学习增强AGCN (NAPL-AGCN)来学习节点特定模式。由于其最先进的性能,NAPL-AGCN已被集成到各种最新的模型中,如Z-GCNETs [7], STG-NCDE[8]和stamp - s2gcnets[6]。
尽管astgnn具有优越的性能,但它们会产生巨大的计算开销,主要是因为(i)学习自适应邻接矩阵涉及计算每对节点之间的边权,以及(ii)聚合阶段的计算量很大。我们的目标是高效的ASTGNN推理,特别是对于大型图。
2.2 gnn的图稀疏化
随着图的快速增长,gnn的训练和推理成本越来越高。高昂的成本激发了人们对图形稀疏化的兴趣。图稀疏化的目的是从原始的大图中提取一个小的子图。SGCN[16]首先研究了gnn的图稀疏化,即修剪输入图边,并学习了一个额外的DNN代理。NeuralSparse[29]从下游监督信号中修剪任务无关的边,以学习稳健的图表示。最近的一些研究,如UGS[5]和GBET[27],从中奖彩票假设的角度探讨了图稀疏化。
上述工作仅探讨了香草gnn和具有预定义图的非时态数据的图稀疏化。我们的工作的不同之处在于关注具有自适应图架构的时空gnn。
3预备
本节提供了astgnn的代表性架构的快速回顾。
3.1作为图结构的时空数据
根据时空图神经网络研究中的惯例[2,3,6 - 8,11,12,19,21,24 - 26,28],我们将时空数据表示为离散帧序列X,其中G = {V, },其中
![]() 。图G也称为空间网络,由一组节点V和一组边
。图G也称为空间网络,由一组节点V和一组边组成,设|V| =N。然后用邻接矩阵并给出了边缘
![]() ,其中
,其中![]() 的节点特征矩阵维度t 步伐,t= 1,..,T。
的节点特征矩阵维度t 步伐,t= 1,..,T。
给定图G和历史观测
![]()
![]() ,我们的目标是学习一个函数F,它将历史观测映射到下一个H时间步长的未来观测:
,我们的目标是学习一个函数F,它将历史观测映射到下一个H时间步长的未来观测:![]()
其中为所有可学习参数。
3.2空间网络建模G
由于我们专注于空间依赖性的作用,我们解释了时空图神经网络(stgnn)中空间网络的最新建模。
在代表性stgnn[2,12,25]中,对时间步长为푡的空间网络G用其节点特征矩阵푿푡建模的基本方法是图卷积网络(Graph Convolution Networks, GCNs)。单层GCN可以定义为:![]()
其中,![]() 为增加自连接的图的邻接矩阵。
为增加自连接的图的邻接矩阵。是单位矩阵。
是度矩阵。
![]()
是一个可训练参数矩阵。(·)为激活函数。
![]() 为输出。在时间步t上关于输入
为输出。在时间步t上关于输入的所有信息都聚合在
中。
空间网络建模的一个关键改进是采用自适应图卷积网络(AGCNs)来捕获图G中的动态,从而产生自适应时空图神经网络(astgnn)[3,6 - 8,25]。下面,我们简要介绍两种具有代表性的ASTGNN模型——自适应图卷积循环网络(Adaptive Graph Convolutional Recurrent Network, AGCRN)[3]和带变压器的扩展,记为AGFormer。
•AGCRN。它通过将归一化自适应邻接矩阵与节点自适应参数学习(NAPL)相结合来增强GCN层,即NAPLAGCN。
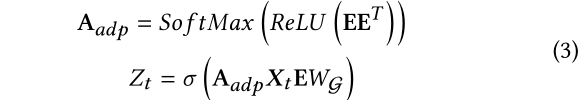
式中,![]() ,
,![]() 。
。![]() 为归一化自适应邻接矩阵[25]。E是
为归一化自适应邻接矩阵[25]。E是![]() 的嵌入尺寸。E的每一行表示节点的嵌入。在训练过程中,更新E以学习所有节点之间的空间依赖关系。NAPL-AGCN不是直接学习由所有节点共享的路由参数(2),而是使用E - G来学习节点特定的参数。从一个节点(例如节点i)的角度来看,
的嵌入尺寸。E的每一行表示节点的嵌入。在训练过程中,更新E以学习所有节点之间的空间依赖关系。NAPL-AGCN不是直接学习由所有节点共享的路由参数(2),而是使用E - G来学习节点特定的参数。从一个节点(例如节点i)的角度来看,![]() 是根据其嵌入的节点
是根据其嵌入的节点对应的节点特定参数。最后,为了捕获空间和时间依赖性,AGCRN集成了NAPL-AGCN和门控循环单元(GRU),用NAPL-AGCN取代GRU中的MLP层。
•AGFormer。它通过对变压器的时间依赖性进行建模来扩展AGCRN[17,22]。变压器是一堆变压器块。一个区块包含一个多头自关注机制和一个完全连接的前馈网络。我们用NAPL-AGCN取代多头自关注机制中的MLP层,构建了一个基于变压器的ASTGNN模型,我们称之为AGFormer。
利用NAPL-AGCN对空间网络建模可以在多个基准上实现最先进的性能,并已广泛应用于各种ASTGNN变体[3,6 - 8]。然而,NAPL-AGCN比GCNs效率低得多,因为![]() 是一个没有零的矩阵,而GCNs中预定义图的邻接矩阵比
是一个没有零的矩阵,而GCNs中预定义图的邻接矩阵比![]() 稀疏得多。这促使我们以astgnn为例,探索时空图模型的局域化。
稀疏得多。这促使我们以astgnn为例,探索时空图模型的局域化。
4自适应图稀疏化
本节介绍了自适应图稀疏化(AGS),这是一种致力于astgnn中邻接矩阵稀疏化的新算法。
配方。具有归一化自适应邻接矩阵![]() 的基于napl - agcn的astgnn可以使用以下目标进行训练:
的基于napl - agcn的astgnn可以使用以下目标进行训练:
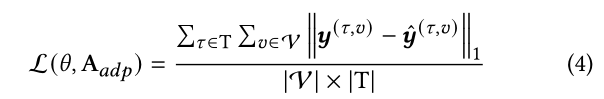
其中T为训练集,为训练样本,
![]() 为
为中节点
的基真值。
给定预训练模型![]() ,我们引入掩码MA对邻接矩阵
,我们引入掩码MA对邻接矩阵![]() 进行剪枝。
进行剪枝。的形状与
![]() 相同。具体来说,给定
相同。具体来说,给定![]() ,我们通过优化以下目标获得
,我们通过优化以下目标获得
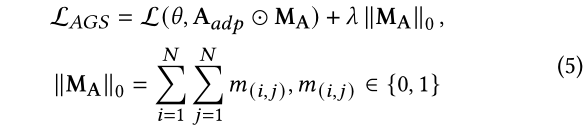
其中⊙是元素积,对应于二进制“门”,表示边缘是否被修剪,
是
-正则化
的权重因子。
Sparsification算法。获得MA的一种直观方法是初始化一个可训练权矩阵![]() ,并使用伯努利分布将条目
,并使用伯努利分布将条目![]() 映射为二进制“门”:
映射为二进制“门”:![]() ,其中B是伯努利分布。然而,将U直接引入模型
,其中B是伯努利分布。然而,将U直接引入模型![]() 有两个问题。
有两个问题。
•对于大规模的图形,它可能是不可伸缩的。
•稀疏性惩罚是不可微的。
对于可扩展性问题,我们采用节点自适应权值学习技术,通过简单地用嵌入E的节点生成U来降低计算成本:
![]()
其中,![]() 是一个可训练矩阵。
是一个可训练矩阵。
对于不可微问题,我们引入了硬混凝土分布,而不是伯努利分布[9],它是离散分布的连续松弛,可以近似二值。
因此,二进制“门”的计算可表示为:
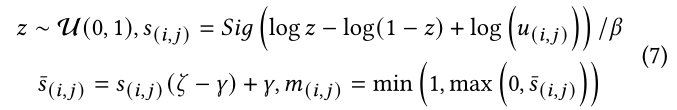
其中z为均匀分布,Sig为sigmoid函数,为温度值,
![]() 为
为![]() 且
且![]() 的区间。我们在实践中设置
的区间。我们在实践中设置![]() 和
和![]() 。然后,应用
。然后,应用来修剪
![]() ,w.r.t.预定义比率푝푔中的最低量级条目。
,w.r.t.预定义比率푝푔中的最低量级条目。
图1概述了AGS的程序。网络预训练后开始剪枝(第5行)。首先,我们按大小升序对邻接矩阵中的边进行排序(第6行)。然后我们迭代地执行剪枝(第7行)。删除顶部的边,保留其余的边。我们通过在每次迭代中将MA中的相应条目设置为1来识别剩余的边(第8行)。使用Eq.(5)(第9行)删除要修剪的边。
讨论。我们对AGS算法做了两点说明。
•AGS不同于先前为图设计的基于幅度的修剪方法[5,27],因为(i)它简化了时空gnn中的自适应图,而不是香草gnn和具有预定义图的非时间数据;(ii)它不需要对修剪后的图进行迭代再训练来恢复模型的准确性。
•使用AGS修剪邻接矩阵显著降低了astgnn推理的复杂性。推理时间未修剪的NAPL-AGCN层的复杂度为![]()
![]() 。稀疏化后,NAPL-AGCN层的推理时间复杂度为
。稀疏化后,NAPL-AGCN层的推理时间复杂度为![]()
![]() ,其中
,其中![]() 为计算自适应邻接矩阵的时间复杂度,d为嵌入维数,N为节点数,
为计算自适应邻接矩阵的时间复杂度,d为嵌入维数,N为节点数,![]() 为剩余边数,
为剩余边数,为节点特征的表示维数,T为输入长度,L为层数。
5实验
为了回答我们是否以及在多大程度上可以定位时空图模型的问题,我们进行了本节中解释的广泛实验。
5.1神经网络架构
我们评估了AGS在两种具有代表性的基于naplagcn的ASTGNN架构上的性能:AGCRN[3]及其扩展AGFormer。AGCRN是结合AGCN和RNN层的最先进的ASTGNN架构。AGCN层用于捕获空间依赖关系,而RNN层用于建模时间依赖关系。另一方面,AGFormer可以看作是AGCRN的替代版本,其中RNN层由Transformer层代替。我们有意选择这两种ASTGNN架构共享相同的空间模块,但使用不同的时间模块,以表明AGS的有效性和我们对学习到的空间依赖性的观察结果与所涉及的时间模块正交。
5.2数据集与配置
astgnn的定位是在来自三个应用领域的九个真实时空数据集上进行评估的:交通运输、区块链和生物监测。表1总结了我们实验中使用的数据集的规格。详细的数据集和配置请参见附录A.1。关于调优超参数的详细信息请参见附录A.2。
5.3主要实验结果
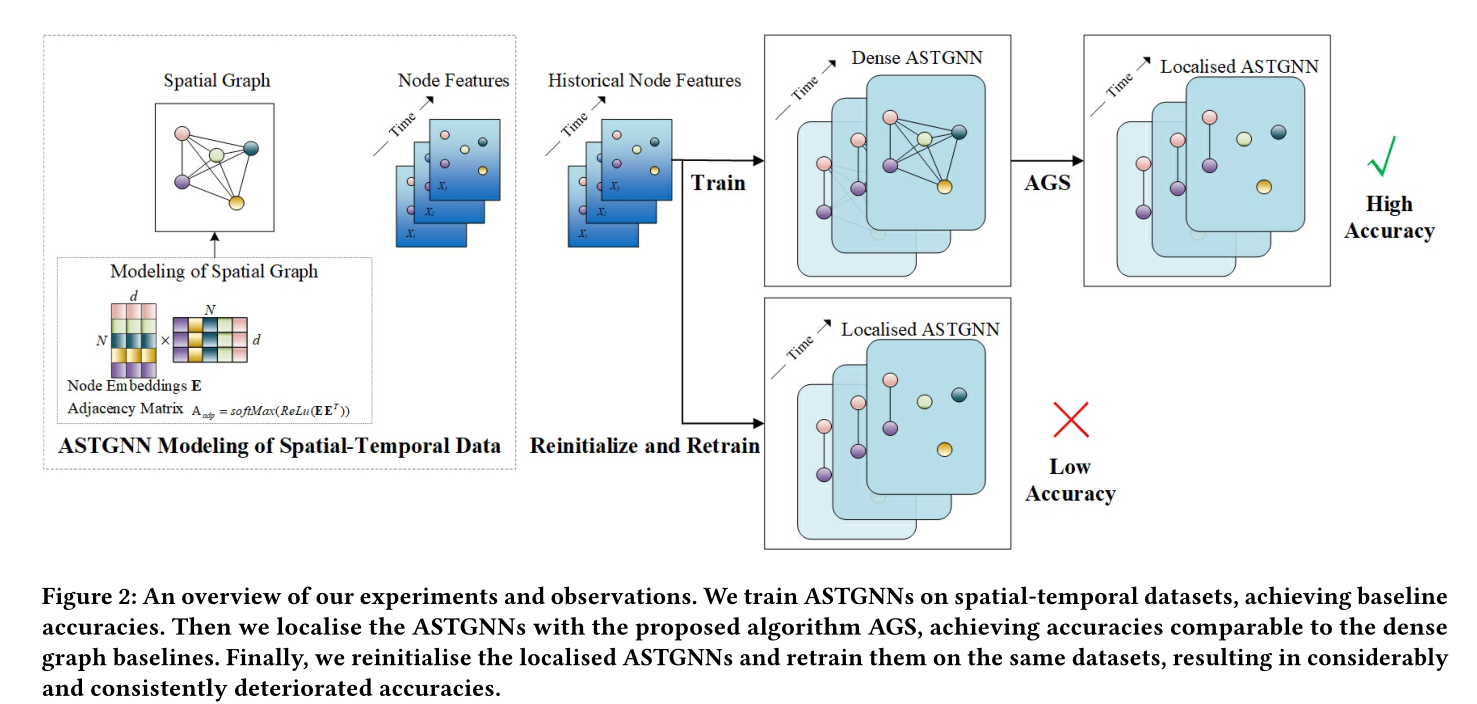
我们的主要实验如图2所示。我们首先在9个时空数据集上训练agcrn和AGFormers,
达到基线精度。然后,我们使用AGS对这些训练有素的agcrn和agformer进行定位。最后,我们重新初始化局部agcrn中的所有权值,并使用相同的训练设置在原始数据集上重新训练它们。
实验结果组织如下:
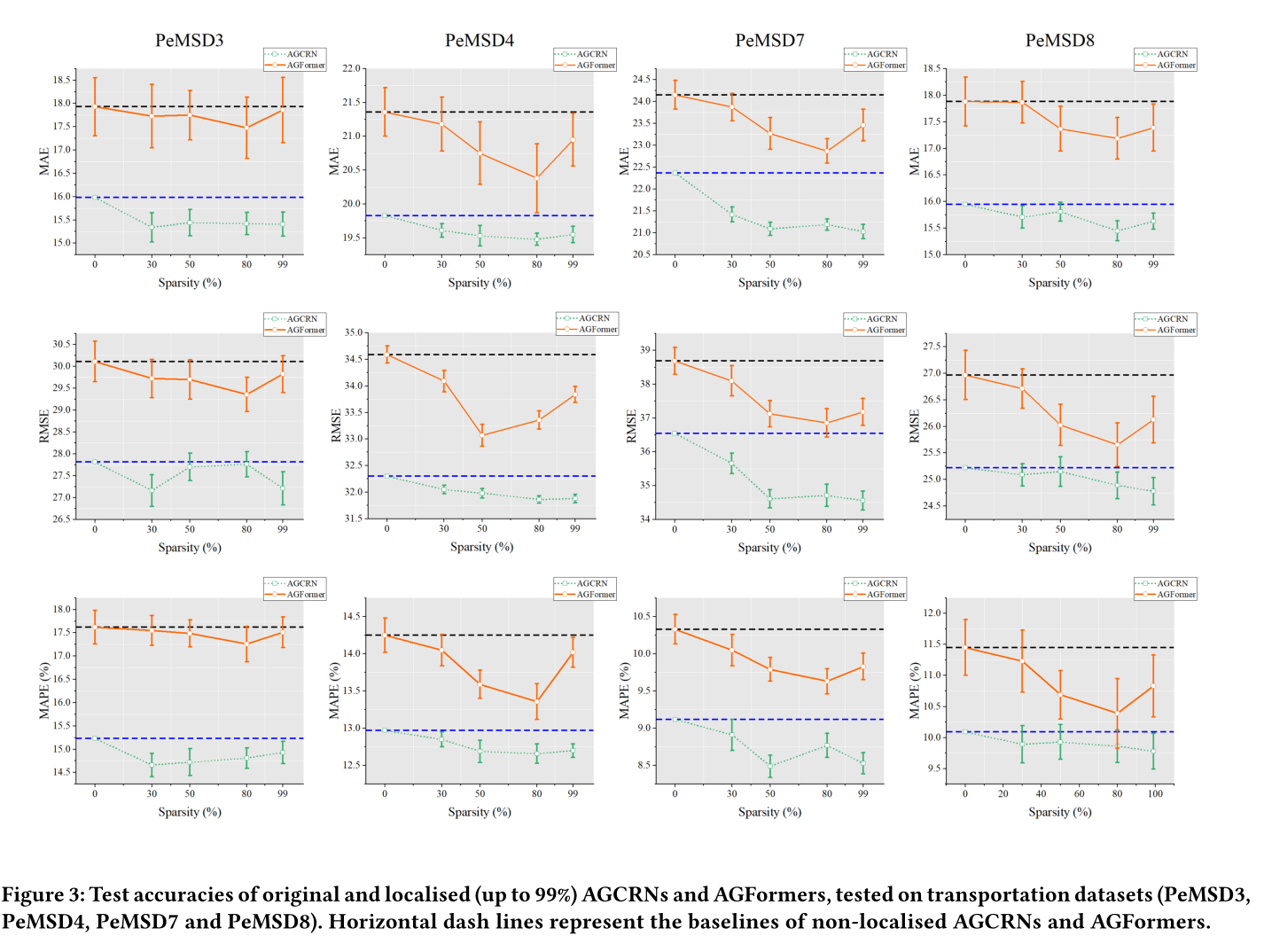
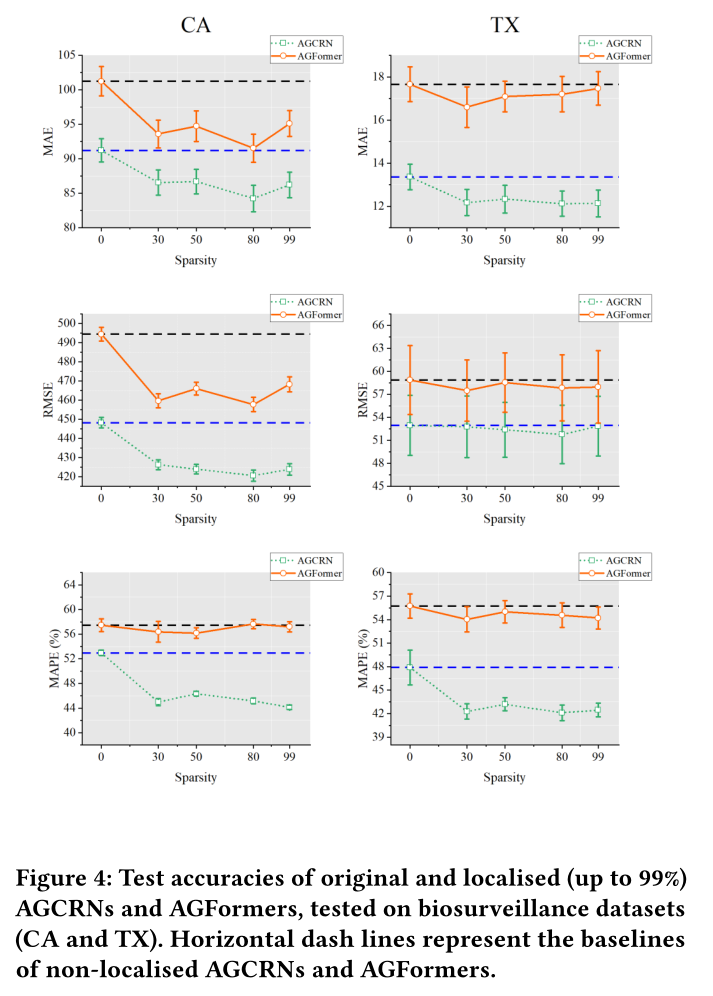
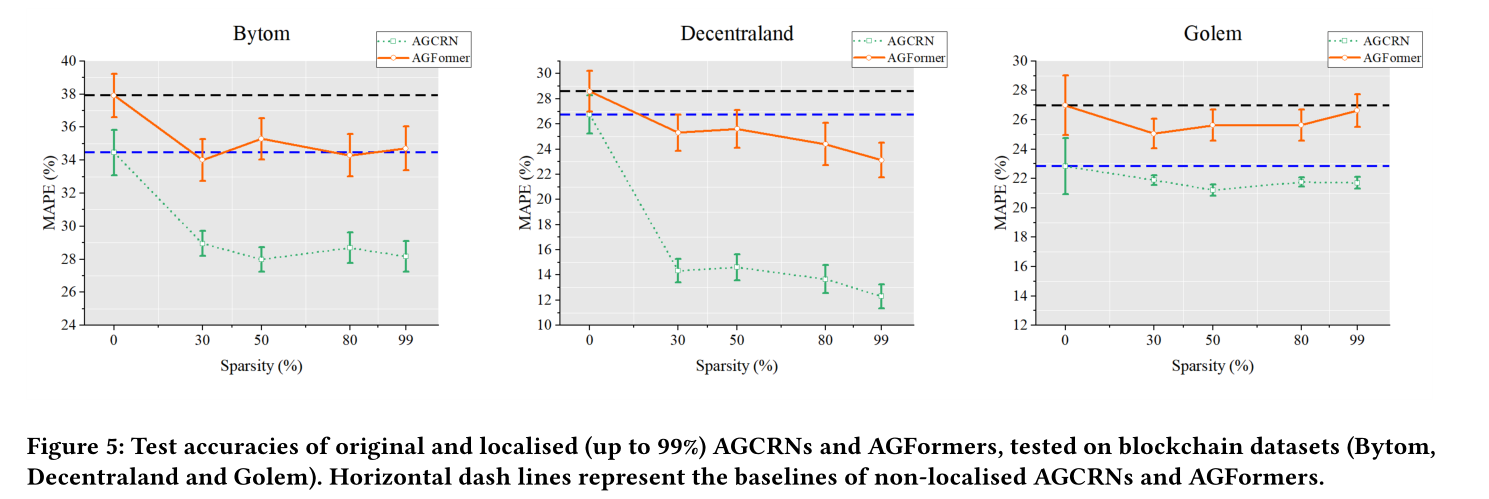
•图3(交通数据集)、图4(生物监测数据集)和图5(区块链数据集)收集了非本地化agcrn和AGFormers以及具有99%本地化程度的agcrn和AGFormers的测试精度。
这些图包含了0%、30%、50%、80%和99%图稀疏度下的测试精度。
•定位度在99.1% ~ 100%之间的agcrn的测试准确率如图6所示,用绿色虚线表示。
•重新初始化和重新训练的局部agcrn的测试精度也收集在图6中,以紫色实线显示。
这些图中的误差条显示了五次运行的标准差。
根据这些结果,我们做了以下观察:
•agcrn和agformer的本地化是可能的。在agcrn和AGFormers上应用AGS并将其定位到99%的定位度不会导致所有数据集的性能下降。相反,在许多实验中,测试精度不断提高,直到99%的定位。与非定位基线相比,进一步定位到99.5%的agcrn仍然不会导致准确性下降。
•agcrn的完全本地化仍然可行。即使我们完全定位了agcrn,这实际上把它们变成了独立的rnn,忽略了所有的空间依赖性,它们仍然可以提供不错的测试精度。如图6所示,在交通数据集(PeMSD3、PeMSD4、PeMSD7和PeMSD8)上,仅观察到轻微的下降。在区块链数据集(Bytom, Decentraland和Golem)和生物监测数据集(CA&TX)上,我们可以观察到,与非局部基线相比,在100%稀疏度下,测试准确性并不差。
•局部agcrn不能在没有密集空间图的情况下重新学习。如图6所示,当我们重新初始化部分或完全定位的agcrn时,然后在9个数据集上重新训练它们,我们可以观察到推理精度的一致和相当大的下降。
基于这些观察结果,我们提出以下假设:•在许多时空数据集中,空间依赖关系提供的信息主要包含在时间依赖关系提供的信息中。因此,可以安全地忽略空间依赖关系来进行推理,而不会有明显的准确性损失。
•虽然空间和时间依赖关系中包含的信息重叠,但这种重叠为正确训练时空图模型提供了重要的冗余。因此,在训练过程中不能忽略空间依赖性。
6 消融研究
6.1对资源效率的影响
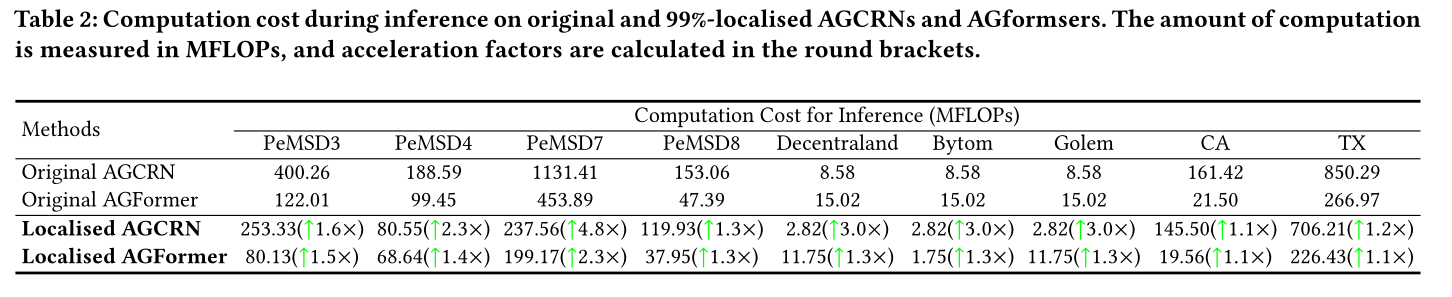
如第1节所述,我们对astgnn本地化特别感兴趣的原因之一是其资源效率。非局域astgnn通常学习完整的空间图。因此,边的数量和计算开销随着顶点的数量呈二次增长。astgnn的定位相当于对学习到的空间图中的边进行剪枝,可以显著降低与空间依赖相关的计算开销,从而提高资源效率。为此,我们计算了99%定位agcrn和agformer在推理过程中的计算量,以FLOPs为单位进行测量,并将结果总结在表2中。我们可以看到agcrn和AGFormers的定位有效地减少了推理所需的计算量。agcrn对agformer的加速更突出,因为agformer所需的总计算量的很大一部分用于它们的时间模块(变压器层),而agcrn使用更轻的时间模块(RNN层)。
6.2定位的agcrn与其他非定位的astgnn
在图3、图4和图5中,我们可以清楚地看到,高达99%的定位能够略微提高测试精度。例如,99%定位的agcrn优于非定位的agcrn,在PeMSD3上降低了3.6%/3.7%/2.0%的RMSE/MAE/MAPE。
这种改善在agcrn和AGFormers以及所有测试数据集中都得到了一致的观察。我们认为这种改善是由空间图稀疏化的正则化效应引起的,这可能表明非局域agcrn和agformer都存在一定程度的过拟合。
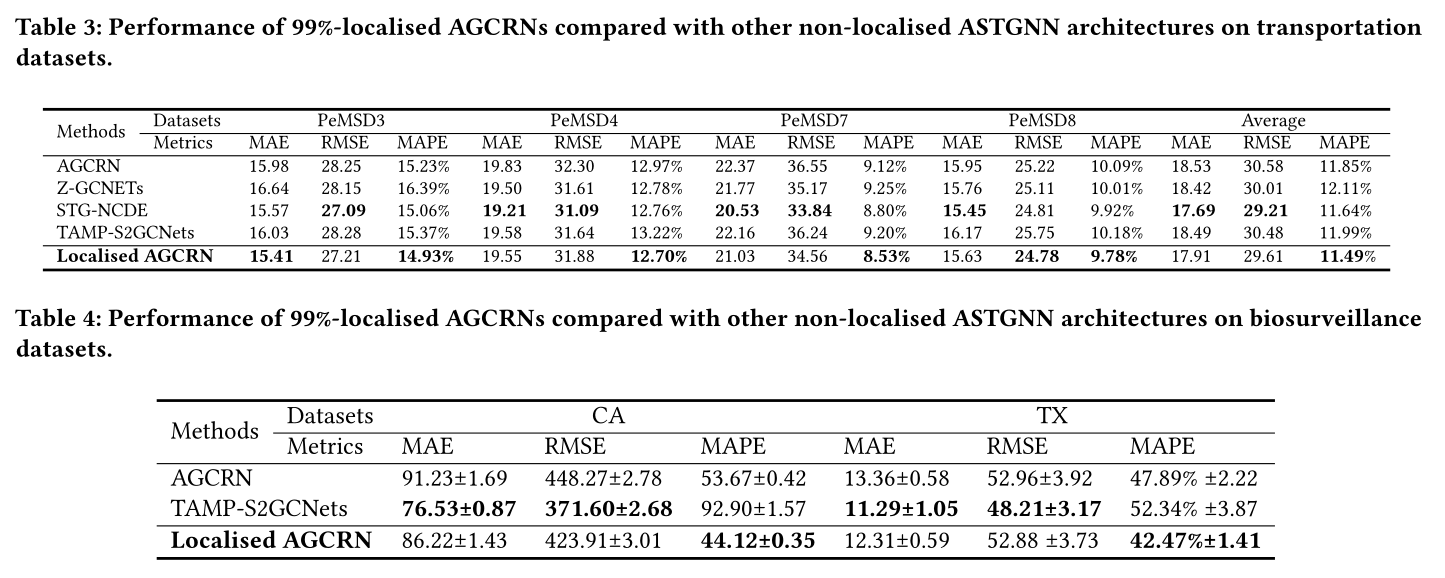
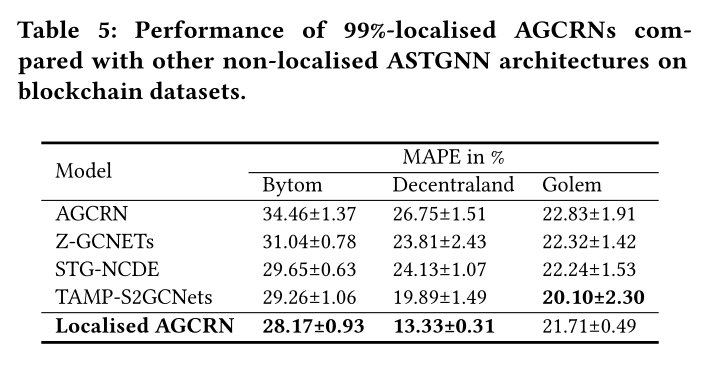
最近关于astgnn的研究提出了AGCRN的改进架构,包括针对不同应用的Z-GCNETs[7]、STG-NCDE[8]和TAMPS2GCNets[6]。因此,我们很好奇我们的局部agcrn如何与这些变异进行比较。
因此,我们比较了99%定位agcrn与这些架构的测试准确性。结果如表3、表4、表5所示。我们可以看到,即使与最先进的架构提供的推理性能相比,我们的本地化agcrn通常也可以提供有竞争力的推理性能。这一观察结果也与我们在5.3节中提到的第一个假设相一致:在许多时空数据集中,空间依赖关系提供的信息主要包含在时间依赖关系提供的信息中。因此,在时间模块得到适当训练的情况下,不同的空间模块在推理性能上可能不会产生显著差异。
6.3非时序图的局部化
为了进一步研究空间依赖性并间接检验我们的假设,我们进行了额外的实验,并将AGS扩展到非时间图。我们尝试对非时态数据集预先给出的空间图进行稀疏化,包括Cora、CiteSeer和Pubmed[20]。在这些数据集上,我们训练了两个非时态图神经网络架构GCN[14]和GAT[23]。在GCN和GAT上,由于它们没有自己的节点嵌入E,我们可以使用预训练GCN和GAT学习到的表示H来替换(6)中的E,然后像在图1中那样修剪边缘,其中权重因子휆控制图的稀疏性。
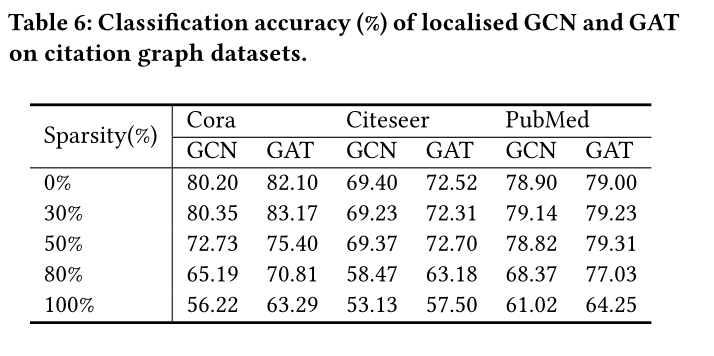
表6显示了本地化GCN和GAT非时态数据集的准确性。Cora、Citeseer和PubMed的预定义图形分别被细化为30%、50%、80%和100%。
我们可以观察到,在所有的测试精度显著下降局域化非时态图模型。这表明,在没有时间依赖的情况下,空间依赖提供的信息在推理过程中起着重要作用,因此不能通过定位忽略。
7结论
在本文中,我们提出了以下问题:我们是否可以以及在多大程度上局部化时空图模型?为了方便我们的研究,我们提出了AGS,一种致力于astgnn中邻接矩阵稀疏化的新算法。我们使用AGS对AGCRN和AGFormer两种ASTGNN架构进行了定位,并在9个不同的时空数据集上进行了广泛的实验。初步实验结果表明,在所有数据集上,空间邻接矩阵可以被稀疏到99.5%以上,且测试精度没有下降。此外,当astgnn完全定位时,我们仍然观察到大多数测试数据集的准确性没有下降,而其余数据集的准确性只发生了轻微的下降。基于这些观察结果,我们提出了关于空间和时间依赖关系的两个假设:(i)在测试数据中,空间依赖关系提供的信息主要包含在时间依赖关系提供的信息中,因此在推理中基本上可以忽略;(ii)尽管空间依赖关系提供了冗余信息,但它对于astgnn的有效训练至关重要,因此在训练过程中不能忽视。最后但并非最不重要的是,我们进行了额外的消融研究,以显示ASTGNN本地化对资源效率的实际影响,并进一步从不同角度验证我们的假设。
这篇关于局部自适应时空图神经网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









