本文主要是介绍139.乐理基础-一四五八度为何用纯?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上一个内容:138.乐理基础-等音、等音程的意义-CSDN博客
上一个内容里练习的答案:

以乐理里写的知识,没办法完全解释透彻 一四五八度为何用纯?这个问题,要透彻的话要从各个文明怎么发现音高、发明音高、制定规则等,一些历史行为和方式去写,会扯到律制、律学的问题,这个要解释会很麻烦,乐理里肯定容纳不下那么多内容,所以只能做一些极简的概述,引用一些结论和侧面的例子,来简单写一下这个问题
所以本次内容即使完全不懂,无法理解,也没有关系,现在只需要死记住二三六七度分大、小,一四五八度只有纯。
首先传统意义上的声音都是通过物体振动来发出声音的,比如弦乐器不管是拉、弹、拔还是其它什么方式,最终都是因为弦的振动而发出声音,再比如各种管乐器,通过不同的激励方式比如簧片激励、唇激励等,最终引起空气振动,从而发出声音,钢琴也是通过击弦的操作来引起弦的振动。
而振动的频率是又快有慢的,每秒钟振动的次数被称为赫兹,赫兹越大,音高越高,赫兹越小,音高越低。
然后又一个古希腊数学家、哲学家 毕达哥拉斯:
传闻中有一天,它在听到铁匠们,叮叮咚咚的打铁声时,就发现了一个当时并没有任何解释的事情,就是明明铁匠们敲的都是铁,但为什么敲出来的音有高有低(这里可以敲打玻璃碗或玻璃杯等物品模拟一下),总之它根据这个现象所研究出来的第一步成果,就是发现了物体振动的弦长越长,赫兹就越低,物体振动的弦长越短,赫兹就越高,这两者成反比,比如一根弦长30厘米,拨动它,拨动之后发出的声音假设称为α音(这时没有CDEFGAB这些音名),然后振动频率就假设成n赫兹,然后毕达哥拉斯经过多次试验与验证就发现了如果再取一根15厘米的弦,长度刚好是30厘米的一半,那这个15厘米的弦发出的振动频率就是2n赫兹,把它假设成β音,这俩跟弦除了长度不同其它都一样,毕达哥拉斯就发现长度缩短成二分之一,频率就正好变为原来的两倍,而且这样两根频率呈两倍关系的弦,发出的音是极其协和,现代把这种音称为纯八度,然后这种1比2频率毕达哥拉斯研究完之后它就又研究其它比例的音,2比3,然后首先还是30厘米,30里面的二分之三是20里面的弦,然后就是二分之三n的赫兹,也就是纯五度。这里有一个五度相生律
五度相生律:找八度以内的音:
通过1比2就得出了纯八度

通过2比3就得出了纯五度的音

然后这个二分之三n在通过2比3的比例,可以得到四分之九n

四分之九n已经大于2n了,比2n纯八度高了,现在研究的是八度以内,所以再通过1比2比例把四分之九n变成八分之九n,然后就回到了八度以内

现在称之为大二度
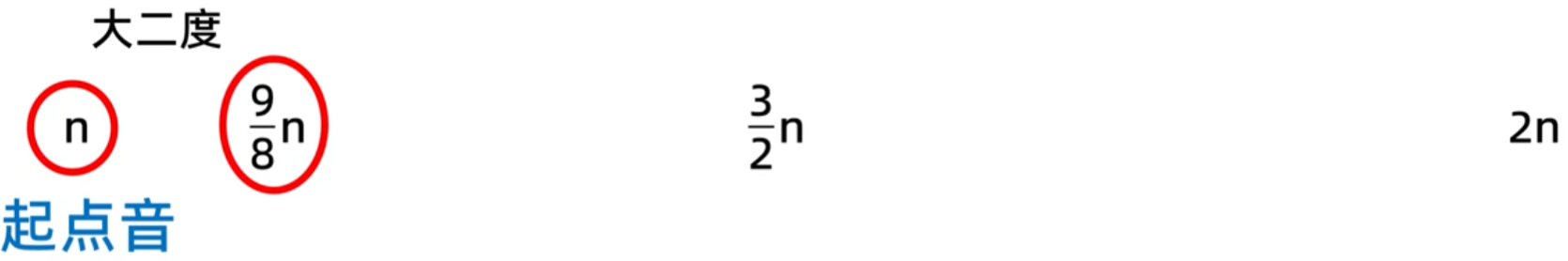
然后再把八分之九n用2比3的比例,就可以得到十六分之二十七n

现在成为大六度

下方是通过上面1比2与2比3的算法,推到31次后,诞生的音:
转化为现代的音名:
现在广泛使用的是十二平均律不是五度相生律,所以很多音的频率关系跟十二平均律相比会有细小的差异(不同律制下,各个音的音高是有略微差异的),如下图,升C和降D本来就不是同一个音,本来就不是同一个频率,这也是等音程不能相互替换的一个原因,即便在十二平均律里它们是相同的频率,但涉及到调式、音程、和弦等使用意义上的区别,升C和降D就算是在十二平均律里也不能随意替换

一四五八度为何用纯?
除了下图圈起来的音,没有简单的频率比了,圈起来的音就是纯一四五八度,它们的频率在1比2、2比3、3比4里
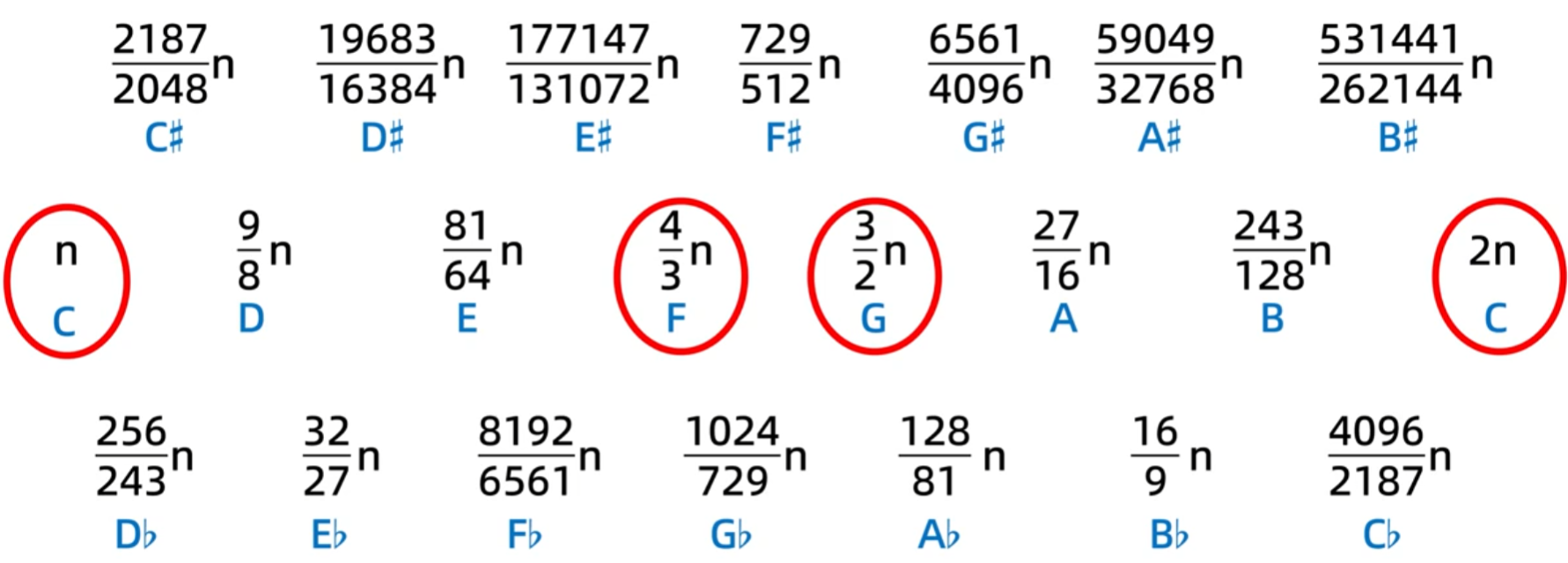
其它的频率比最简单的都要8比9,8比9就称不上简单的频率比了,比8比9还要离谱的频率比也就更复杂了
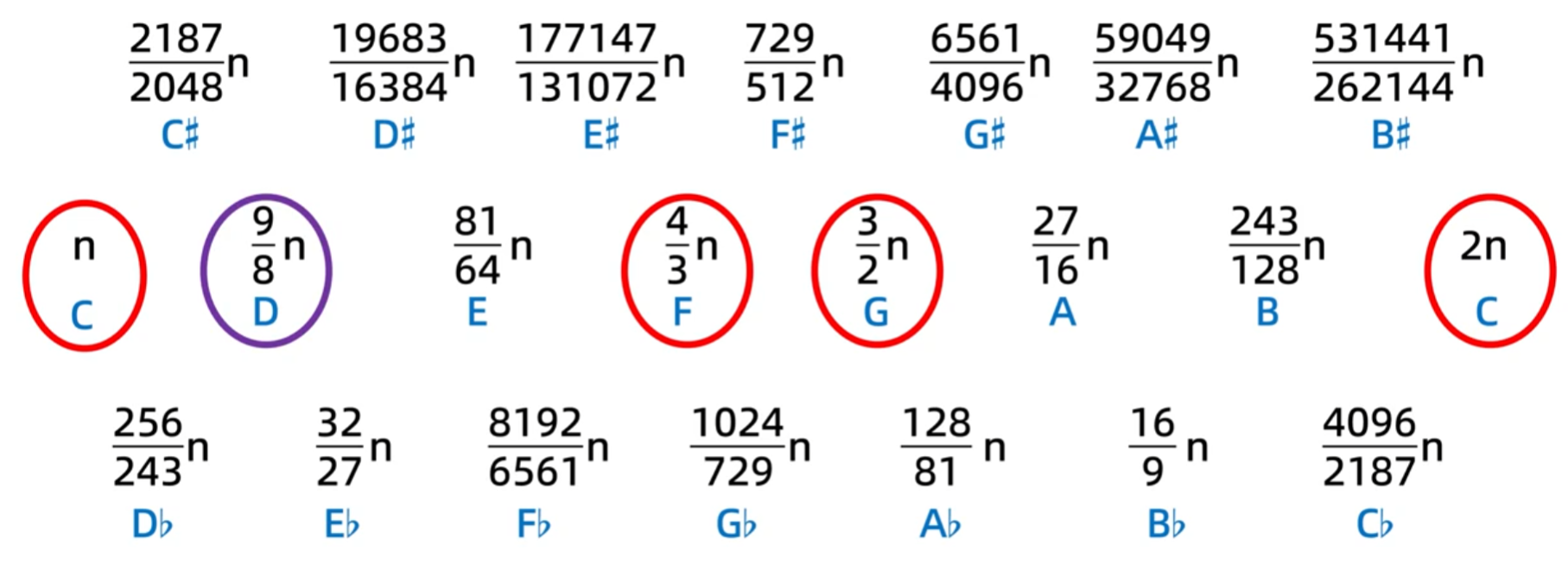
一四五八度会用纯本质原因就是频率比越简单,音越协和
五度相生律计算出的音是回不到2n的,如下图,目前没有完美的律制

练习:找音程


这篇关于139.乐理基础-一四五八度为何用纯?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








