本文主要是介绍Matlab|【免费】基于合作博弈的综合能源系统利益分配优化调度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
主要内容
部分代码
结果一览
下载链接
主要内容
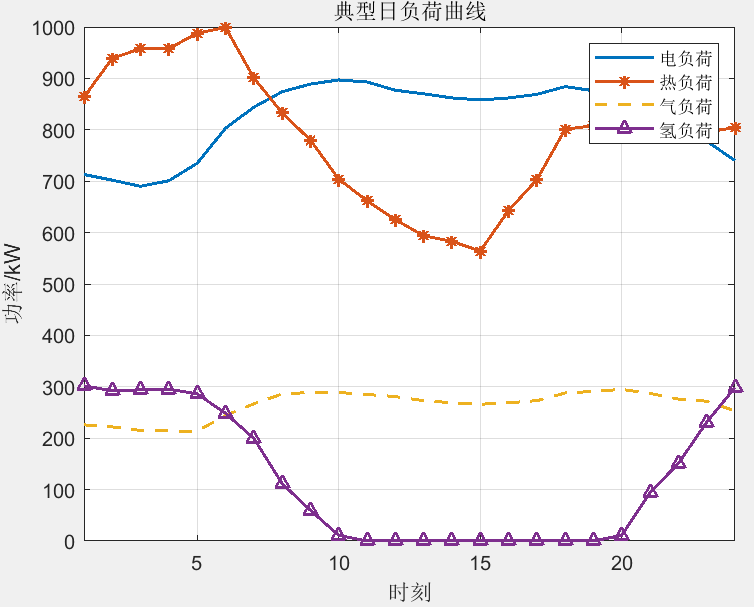
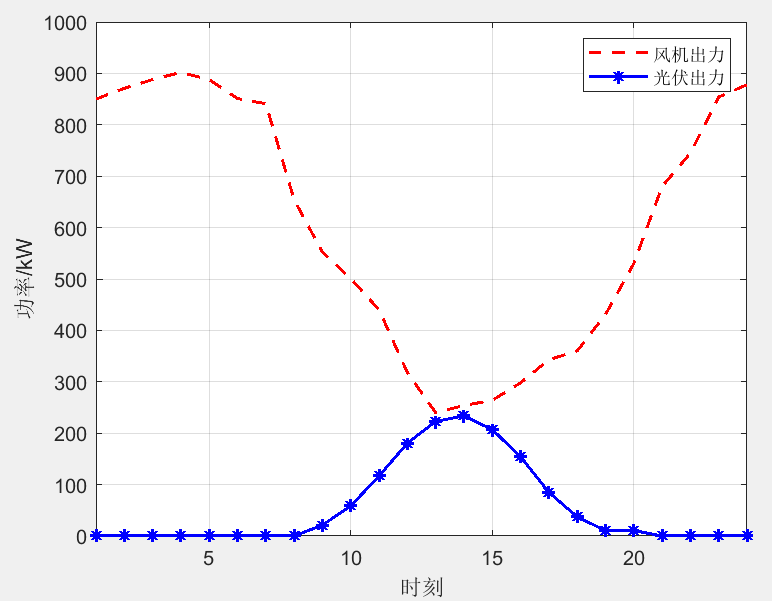
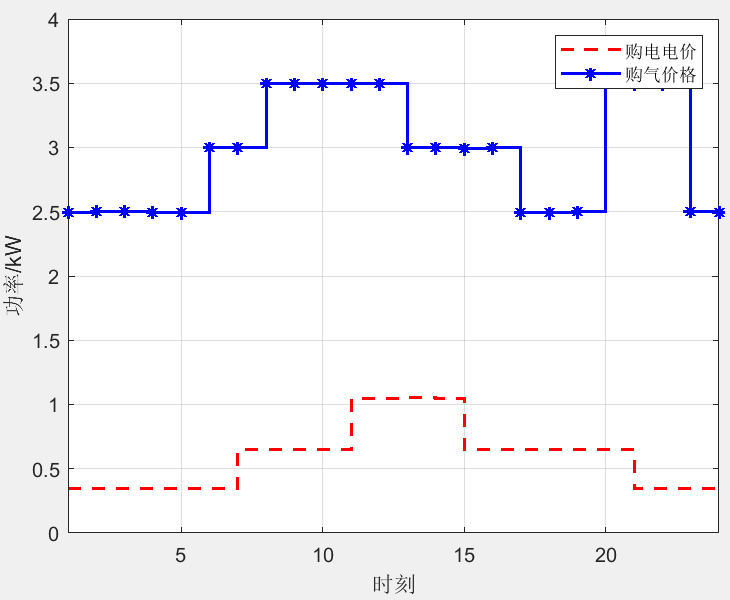
该程序实现的模型为综合能源系统利益分配优化调度,采用合作博弈方法,模型针对IES系统的P2G、电解槽、甲烷反应器、储氢罐、CHP和燃气锅炉等设备进行建模,实现基于合作博弈的IES协同优化调度模型,利用Shapley值法对合作剩余按贡献进行分配,程序采用matlab+cplex求解,程序注释清楚,方便学习!
部分代码
%% 决策变量定义P_wt=sdpvar(1,T); %风机消纳功率P_pv=sdpvar(1,T); %光伏消纳功率V_gas=sdpvar(1,T); %P2G产生天然气体积Q_co2=sdpvar(1,T); %制气厂消耗二氧化碳的量P_H2=sdpvar(1,T); %电解池产生的氢气量P_P2G=sdpvar(1,T); %P2G消耗电功率量P_h2cha=sdpvar(1,T); %储氢罐充气功率P_h2dis=sdpvar(1,T); %储氢罐放气功率H_h2cha=binvar(1,T); %储氢罐充气变量H_h2dis=binvar(1,T); %储氢罐放气变量P_H2total=sdpvar(1,T);E_h=sdpvar(1,T); %储氢罐放气功率P_CHPe=sdpvar(1,T); %CHP发电功率P_CHPh=sdpvar(1,T); %CHP发热功率P_CHPg=sdpvar(1,T); %CHP耗气功率Q_co2out=sdpvar(1,T); %CHP燃烧产生的co2P_be=sdpvar(1,T); %购电功率P_bg=sdpvar(1,T); %购气功率V_CB=sdpvar(1,T); %燃气锅炉进气量Q_CB=sdpvar(1,T); %燃气锅炉发热量P_MRh=sdpvar(1,T); %甲烷反应器输入氢功率P_MRg=sdpvar(1,T); %甲烷反应器输出天然气功率%% 风光模型C=[C,0<=P_wt<=S_w];C=[C,0<=P_pv<=S_p];%% P2G设备运行模型C=[C,Q_co2==alpha_co2*nita_ch4*load_H];C=[C,P_H2==nita_H2*P_P2G]; %电解槽产生氢气功率C=[C,P_H2total==P_H2+P_h2dis-P_h2cha];C=[C,0<=P_H2<=500];%% 甲烷反应器运行模型C=[C,P_MRg==nita_ch4*P_MRh]; %电解槽产生氢气功率C=[C,0<=P_MRg<=250];%% 储氢罐模型C = [C, H_h2dis + H_h2cha <= 1];C = [C, 0 <= P_h2cha <=H_h2cha*50];C = [C, 0 <= P_h2dis<= H_h2dis*50];for t = 2:24C = [C, E_h(t) == E_h(t-1) + 0.9*P_h2cha - P_h2dis/0.9];endC = [C, 0.1 <= E_h(:)/200 <= 0.9];C = [C, E_h(1)==E_h(24)];%% CHP运行约束C=[C,P_CHPe==P_CHPg*CHP_e];C=[C,P_CHPh==P_CHPg*CHP_h];C=[C,Q_co2out==P_CHPg*alpha_co2];C=[C,0<=P_CHPg<=600];for t=1:1:23C=[C,-50<=P_CHPg(t+1)-P_CHPg(t)<=50];end%% 燃气锅炉约束C=[C,Q_CB==K_gas*nita_CB*V_CB];C=[C,0<=Q_CB<=800];for t=1:1:23C=[C,-100<=Q_CB(t+1)-Q_CB(t)<=100];end%% 功率平衡约束C=[C,0<=P_be<=1000];C=[C,0<=P_bg<=1000];%电功率平衡C=[C,load_e+P_P2G==P_wt+P_pv+P_CHPe+P_be];%热功率平衡C=[C,load_h==P_CHPh+Q_CB];%气功率平衡C=[C,load_g+P_CHPg+V_CB==P_MRg+P_bg];%氢功率平衡C=[C,load_H+P_MRh==P_H2+P_h2dis-P_h2cha];
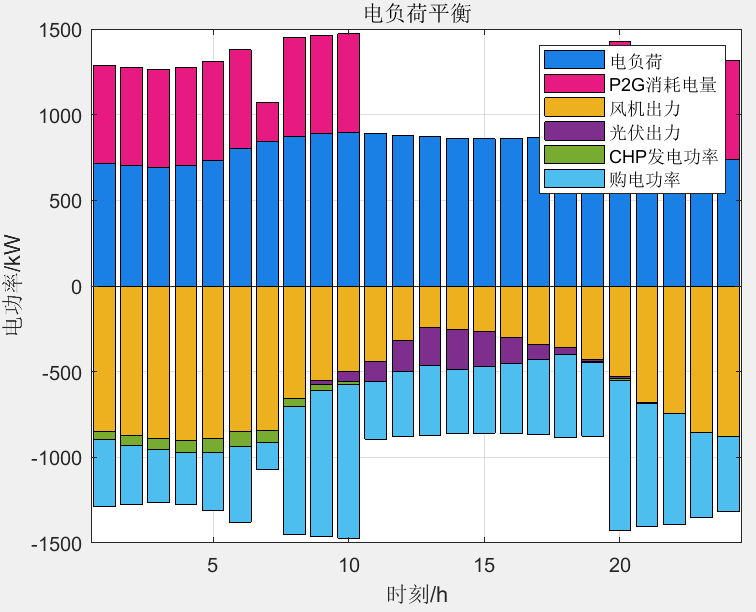
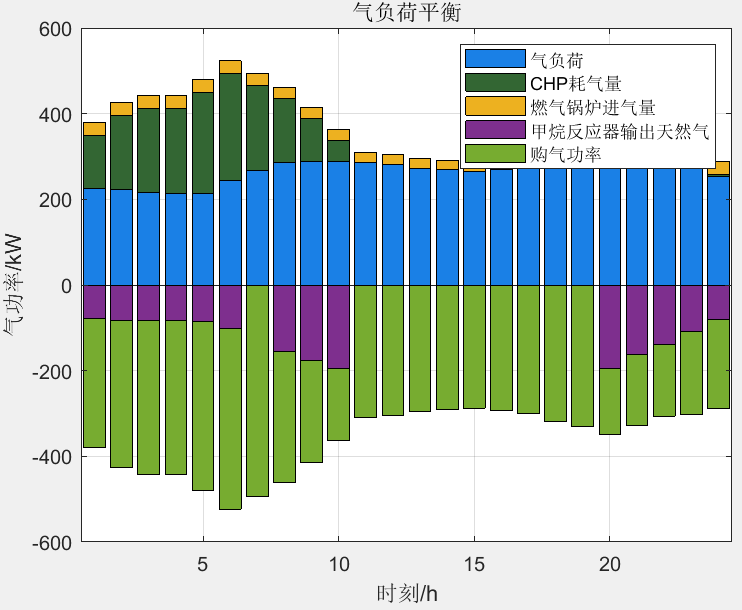
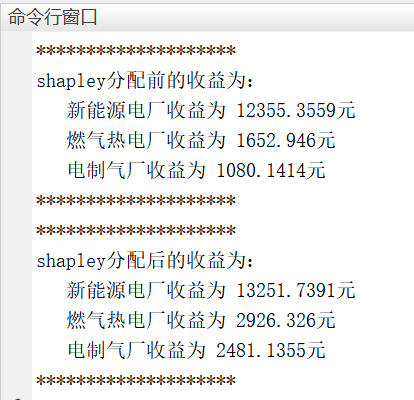
结果一览
下载链接
这篇关于Matlab|【免费】基于合作博弈的综合能源系统利益分配优化调度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!