代码随想录算法训练营14期第2天| 977.有序数组的平方 ，209.长度最小的子数组 ，59.螺旋矩阵II

977. 有序数组的平方https://leetcode.cn/problems/squares-of-a-sorted-array/

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

解题1：暴力破解法

首先可以用自带的Sort函数直接进行求解，也就是暴力破解法：

class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {for (int i = 0; i < nums.size();i++){nums[i] *= nums[i];}sort(nums.begin(), nums.end()); //快速排序方法return nums;  //C++的最后，别忘了return结果，不要还是老习惯};
};

时间复杂度：比较好理解，看到卡哥书上写的这里的时间复杂度度是O(n+nlogn)，这里

解题2：双指针法

看到书本上写了时间复杂度为O（n）的方法，故在这里也尝试一下

class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {vector<int> result(nums.size(), 0);int k = nums.size() - 1;for (int i = 0, j = nums.size() - 1;i <= j;){ //j的取值必须为nums.size() - 1，否则会        //报错，见后面if (nums[i] * nums[i] < nums[j] * nums[j]){result[k--] = nums[j] * nums[j];j--;}else if (nums[i] * nums[i] >= nums[j] * nums[j]){result[k--] = nums[i] * nums[i];i++;}else break;}return nums;};
};

感悟：

1.双指针法的优势在于，和一般先遍历获取信息的算法不同，双指针可以直接在第一次遍历的时候完成排序任务，减少了后续的操作，为此极大增强了其时间效率。

但是在处理时同样，其空间复杂度比前者要高，属于一种以空间换时间的做法

2.另外，j的区间一定要弄对，如果弄不对的话就会出现如下报错信息

因为C++语言处理比较底层（大概吧），所以错误信息没有那么好弄懂。这里的错误信息发生的原因在于j在跃出nums的容量时，vector型容器nums会分配一个新的空间，而在这个空间中的新的值就是-1094795586，其平方超过了21亿的int区间，所以会报错

Line 7: Char 45: runtime error: signed integer overflow: 
-1094795586 * -1094795586 cannot be represented in type 'int' 
(solution.cpp)SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:16:45

209. 长度最小的子数组https://leetcode.cn/problems/minimum-size-subarray-sum/

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

解题1：暴力破解法

首先仍然是暴力破解法，以i为起始点，j为终止点：

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int length = 0;int sum = 0;int result = INT32_MAX;for (int i = 0; i < nums.size();i++){sum = 0;for (int j = i; j < nums.size(); j++){sum += nums[j];if (sum >= target){length = j - i + 1;result = result < length ? result: length;break;}}}return result == INT32_MAX ? 0 : result; //冒号前为条件判定语句，条件成立则范围问号后的值//冒号后为默认赋值}
};

此方法中，时间复杂度为O(n)

解题2：滑动窗口法

和双指针思想类似，滑动窗口方法在改变双指针位置时便做到了条件判定，减少了迭代时间。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int length = 0;int sum = 0;int result = INT32_MAX;int i = 0;for (int j = i; j < nums.size(); j++){sum += nums[j];while (sum >= target){length = j - i + 1;result = result < length ? result: length;sum -= nums[i];i++;}}return result == INT32_MAX ? 0 : result; //冒号前为条件判定语句，条件成立则范围问号后的值//冒号后为默认赋值}
};

感悟：

1.第二种方法的优势还是在于时间复杂度，为O(n)，按照卡哥的说法，所有的元素都被遍历过了2次，所以时间复杂度应该为O(2n)

59. 螺旋矩阵 IIhttps://leetcode.cn/problems/spiral-matrix-ii/

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

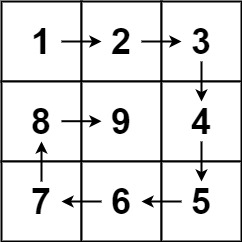
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> nums(n, vector<int> (n, 0)); //定义2维vector的方式int count = 1;int start_x, start_y =0;int offset = 1;int loop = n / 2;while (loop --){for (int j = start_y; j < n -offset; j++){ //第一圈offset应当为1，否则会溢出nums[start_x][j] = count++;}for (int i = start_x; i < n -offset; i++){nums[i][n - offset] = count++;}for (int j = n - offset; j > start_y; j--){nums[n - offset][j] = count++;}for (int i = n - offset; i > start_x; i--){nums[i][start_y] = count++;}start_y ++;start_x ++;offset ++;}if (n%2){nums[n/2][n/2] = count;}return nums;}
};