信号系统之快速傅里叶变换

本文主要是介绍信号系统之快速傅里叶变换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 使用复数DFT的实数DFT

本文的主题，如何使用 FFT 计算真正的 DFT？

由于 FFT 是一种用于计算复数 DFT 的算法，因此了解如何将实数 DFT 数据输入和输出复数 DFT 格式非常重要。图 12-1 比较了实数 DFT 和复数 DFT 存储数据的方式。实数 DFT 将一个 N 点时域信号转换为两个 N/2+1 点频域信号。​频域中的两个信号称为实部和虚部，分别保持余弦波和正弦波的幅度。

相比之下，复数DFT将两个N点时域信号转换为两个N点频域信号。两个时域信号称为实部和虚部，就像频域信号一样。

假设有一个 N 点信号，并且需要通过复数 DFT 计算实际 DFT。首先，将 N 点信号移动到复数 DFT 时域的实部，然后将虚部中的所有样本设置为零。计算复数 DFT 后，在频域中产生一个实数和一个虚数信号，每个信号由 N 个点组成。这些信号的样本 0 到 N/2 对应于真实 DFT 的频谱。

当包含负频率时，DFT的频域是周期性的。单一时期的选择是任意的；它可以在 -1.0 和 0、-0.5 和 0.5、0 和 1.0 之间选择，也可以在任何其他以采样率为基准的单位间隔之间进行选择。复数 DFT 的频谱包括 0 到 1.0 排列中的负频率。换言之，一个完整的周期从样本 0 延伸到样本 N-1，相当于采样率的 0 到 1.0 倍。正频率介于样本 0 和 N/2 之间，对应于 0 到 0.5。其他样本，介于 N/2+1 和 N-1 之间，包含负频率值（通常被忽略）。

使用复数逆 DFT 计算真正的逆 DFT 稍微困难一些。这是因为需要确保以正确的格式加载负频。复数 DFT 中的点 0 到 N/2 与实数 DFT 中的点相同，无论是实部还是虚部。对于实部，点 N/2+1 与点 N/2-1 相同，点 N/2+2 与点 N/2-2 相同，依此类推。这继续表明 N-1 点与点 1 相同。虚部使用相同的基本图案，只是符号发生了变化。也就是说，点 N/2+1 是点 N/2-1 的负数，点 N/2+2 是点 N/2-2 的负数，依此类推。请注意，样本 0 和 N/2 在此复制方案中没有匹配点。在实践中，将真实 DFT 的频谱加载到复数 DFT 阵列的样本 0 到 N/2 中，然后使用子程序在样本 N/2+1 和 N-1 之间生成负频率。表 12-1 显示了这样的程序。为了检查是否存在适当的对称性，在进行逆 FFT 后，查看时域的虚部。如果一切都正确，它将包含所有零（除了百万分之几的噪声，使用单精度计算）。

2 FFT 的工作原理

FFT 是一种复杂的算法，其细节通常留给专门研究此类事物的人。本节介绍FFT的一般操作，但忽略了一个关键问题：复数的使用。

在复数记数法中，时域和频域各包含一个由 N 个复点组成的信号。这些复点中的每一个都由两个数字组成，即实部和虚部。例如，当谈论复样本 X[42] 时，它指的是 ReX[42] 和 ImX[42] 的组合。换句话说，每个复变量包含两个数字。当两个复变量相乘时，必须将四个单独的分量组合在一起以形成乘积的两个分量。

FFT 的工作原理：

• 将 N 点时域信号分解为 N 个时域信号，每个时域信号由一个点组成。
• 第二步是计算与这些N个时域信号对应的N个频谱。
• 最后，将 N 频谱合成为单个频谱。

图 12-2 显示了 FFT 中使用的时域分解示例。在此示例中，一个 16 点信号通过 4 个独立的阶段。

• 第一阶段将 16 点信号分成两个信号，每个信号由 8 个点组成。
• 第二阶段将数据分解为4个点的4个信号。这种模式一直持续到有 N 个信号由单个点组成。每次将信号一分为二时，都会使用隔行分解，即将信号分成偶数和奇数样本。理解这一点的最好方法是检查图 12-2。这种分解需要 $Lo{g}_{2}N$ 级，即 16 点信号($2^4$)需要 4 级，512 点信号($2^7$)需要 7 级，4096 点信号($2^{1}2$)需要 12 级，以此类推。

分解无非是信号中样本的重新排序。图 12-3 显示了所需的重排模式:

• 在左侧，列出了原始信号的样本编号及其二进制等效物。
• 在右侧，列出了重新排列的样本编号，以及它们的二进制等价物。

重要的想法是二进制数是彼此的反转。例如，样本3(0011)与样本12(1100)交换。同样，样本14(1110)与样本7(0111)交换，依此类推。FFT时域分解通常通过比特反转排序算法进行。这涉及通过以二进制方式计数，将位从左翻转为右翻转（例如在图 12-3 中最右边的列中）来重新排列 N 个时域样本的顺序。

FFT 算法的下一步是找到 1 点时域信号的频谱。没有比这更容易的了；1点信号的频谱等于自身。这意味着执行此步骤不需要任何内容。现在 1 点信号中的每一个都是频谱，而不是时域信号。

FFT 的最后一步是以与时域分解发生的完全相反的顺序组合 N 频谱。这就是算法变得混乱的地方。不幸的是，位反转快捷方式不适用，必须一次返回一个阶段。第一阶段，将16个频谱(每个1点)合成为8个频谱(每个点2点)。在第二阶段，将 8 个频谱(每个 2 点)合成为 4 个频谱(每个 4 点)，依此类推。最后阶段产生 FFT 的输出，这是一个 16 点频谱。

图 12-4 显示了如何将两个频谱（每个频谱由 4 个点组成）组合成一个由 8 个点组成的单个频谱。这种合成必须撤消在时域中完成的隔行分解。换言之，频域操作必须对应于通过隔行扫描组合两个 4 点信号的时域过程。考虑两个时域信号，abcd 和 efgh。8 点时域信号可以通过两个步骤形成：

• 用零稀释每个 4 点信号，使其成为8点信号，然后将信号加在一起。也就是说，abcd 变为 a0b0c0d0，efgh 变为 0e0f0g0h。
• 将这两个 8 点信号相加会产生 aebfcgdh。如图12-4所示，用零稀释时域对应于频谱的重复。

因此，在FFT中，通过复制频谱，然后将复制的频谱相加，在FFT中进行组合。

为了在添加时匹配，两个时域信号以略有不同的方式用零稀释。在一个信号中，奇数点为零，而在另一个信号中，偶数点为零。换言之，其中一个时域信号（图12-4中的0e0f0g0h）被一个样本向右移动。这个时域偏移对应于将频谱乘以正弦曲线。时域中的位移等价于使用位移的 delta 函数对信号进行卷积。这会将信号的频谱乘以移位增量函数的频谱。偏移 delta 函数的谱是正弦曲线（见图 11-2）。

图 12-5 显示了将两个 4 点光谱组合成一个 8 点光谱的流程图。为了进一步减少这种情况，请注意，图 12-5 是由图 12-6 中的基本模式一遍又一遍地重复形成的。

这个简单的流程图因其有翅膀的外观而被称为蝴蝶。蝴蝶是FFT的基本计算元件，将两个复点转换为另外两个复点。

图 12-7 显示了整个 FFT 的结构。时域分解是通过比特反转排序算法完成的。将分解后的数据转换为频域不涉及任何内容，因此不会出现在图中。

频域合成需要三个环路。外部循环贯穿 $Lo{g}_{2}N$ 阶段（即图 12-2 中的每个级别，从底部开始并移动到顶部）。中间环路穿过正在处理的阶段中的每个单独的频谱（即图 12-2 中任何一个水平上的每个框）。最里面的环路使用蝶形来计算每个频谱中的点（即，循环遍历图 12-2 中任何一个框内的样本）。图 12-7 中的架空框确定循环的开始和结束索引，以及计算蝴蝶所需的正弦曲线。

3 FFT 程序

可以通过将时域信号与正弦波和余弦波相关联来计算真正的DFT。表 12-2 显示了用相同方法计算复数 DFT 的程序。在同类比较中，这是 FFT 改进的程序。

表 12-3 和 12-4 显示了两个不同的 FFT 程序，一个在 FORTRAN 中，一个在 BASIC 中。首先，将查看表 12-4 中的 BASIC 例程。此子例程产生的输出与表 12-2 中的关联技术完全相同，只是它的速度要快得多。图 12-7 中的框图可用于识别该程序的不同部分。数据被传递到数组中的这个 FFT 子例程：REX[] 和 IMX[]，每个子例程从样本 0 到 N-1 运行。从子例程返回后，REX[] 和 IMX[] 将被频域数据覆盖。这是 FFT 高度优化的另一种方式；输入、中间存储和输出使用相同的数组。这种对存储器的有效利用对于设计快速硬件来计算FFT非常重要。

虽然所有 FFT 程序都产生相同的数值结果，但需要注意编程中的细微变化。表 12-3 中列出的 FORTRAN 程序说明了重要的差异。该程序使用一种称为频率抽取(decimation in frequency)的算法，而前面描述的算法称为时间抽取(decimation in time)。在频率抽取算法中，位反转排序是在三个嵌套循环之后完成的。还有一些 FFT 例程可以完全消除位反转排序。这些变化都没有显著提高 FFT 的性能。

FFT 算法之间的重要区别在于数据如何输入和输出子程序。在 BASIC 程序中，数据进入和离开数组 REX[] 和 IMX[] 中的子程序，样本从索引 0 到 N-1。在FORTRAN程序中，数据在复数组 X() 中传递，样本从1到N。由于这是一个复变量数组，因此 X() 中的每个样本都由两个数字组成，一个实部和一个虚部。DFT 的长度也必须传递给这些子例程。在 BASIC 程序中，变量 N% 用于此目的。相比之下，FORTRAN 程序使用变量 M，该变量定义为等于 $Lo{g}_{2}N$。例如，M 将是 8 表示 256 点 DFT，12 表示 4096 点 DFT，以此类推。关键是，编写 FFT 子例程的程序员有许多与主机程序交互的选项。从 1 到 N 运行的数组（例如在 FORTRAN 程序中）尤其令人恼火。大多数 DSP 文献（包括本书）都解释了假设阵列从样本 0 到 N-1 运行的算法。例如，如果阵列从 1 到 N，则频域中的对称性约为点 1 和 N/2 + 1，而不是点 0 和 N/2。

使用复数 DFT 来计算实际 DFT 还有另一个有趣的优势。复数DFT在时域和频域之间比实际DFT更对称。也就是说，二元性更强。除其他外，这意味着反向 DFT 与正向 DFT 几乎相同。事实上，计算反向 FFT 的最简单方法是计算 Forward FFT，然后调整数据。表 12-5 显示了以这种方式计算逆 FFT 的子例程。

假设将这些 FFT 算法之一复制到计算机程序中并启动它运行。怎么知道它是否正常运行？调试通常使用两种技巧：

• 首先，从一些任意时域信号开始，例如来自随机数生成器的信号，然后通过FFT运行它。接下来，通过反向FFT运行生成的频谱，并将结果与原始信号进行比较。它们应该是相同的，除了舍入噪声（单个精度为百万分之几）。
• 正确操作的第二个测试是信号是否具有正确的对称性。当时域信号的虚部由所有零组成时（正常情况），如前所述，复数DFT的频域将在样本0和N/2周围对称。同样，当频域中存在这种正确的对称性时，逆 DFT 将产生一个时域，该时域的假想部分由所有零（加上舍入噪声）组成。这些调试技术对于使用 FFT 至关重要;熟悉他们。

4 速度和精度比较

当通过相关性计算 DFT 时（如表 12-2 所示），程序使用两个嵌套循环，每个循环运行 N 个点。这意味着操作总数与 N 乘以 N 成正比。因此，完成该计划的时间由以下因素给出：

其中 N 是 DFT 中的点数，$k_{DFT}$ 是比例常数。如果在嵌套循环中计算正弦和余弦值，则 $k_{DFT}$ 等于大约 25 微秒，在 100 MHz 的奔腾上。如果预先计算正弦和余弦值并将它们存储在查找表中，则 $k_{DFT}$ 将下降到大约 7 微秒。例如，一个 1024 点的 DFT 大约需要 25 秒，或者每个点将近 25 毫秒。

使用相同的策略，可以推导出 FFT 的执行时间。位反转所需的时间可以忽略不计。在每个 $Lo{g}_{2}N$ 阶段中，都有 N/2 个蝴蝶计算。这意味着程序的执行时间近似为：

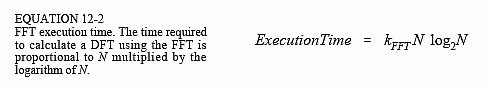
在 100 MHz Pentium 系统上，$k_{FFT}$ 的值约为 10 微秒。一个 1024 点 FFT 大约需要 70 毫秒才能执行，即每个点 70 微秒。这比通过相关性计算的 DFT 快 300 多倍！

$NLo{g}_{2}N$ 不仅小于 N，而且随着 $N^2$ 变大，它的增长速度要慢得多。例如，32 点 FFT 比相关方法快约 10 倍。然而，4096 点 FFT 的速度要快一千倍。对于较小的 N 值（例如，32 到 128），FFT 很重要。对于较大的 N 值（1024 及以上），FFT 绝对至关重要。图 12-8 以图形形式比较了两种算法的执行时间。

除了原始速度之外，FFT 还有另一个优势。FFT 的计算更精确，因为计算次数越少，舍入误差就越小。这可以通过获取任意信号的 FFT，然后通过反向 FFT 运行频谱来证明。这将重建原始时域信号，但从计算中增加了舍入噪声。通过计算两个信号之间差值的标准偏差，可以得到表征该噪声的单个数字。为了进行比较，可以使用通过相关性计算的 DFT 和相应的逆 DFT 来重复相同的过程。FFT的舍入噪声与DFT的相关性如何比较？请看图 12-9 中的亲眼目睹。

5 速度进一步提高

有几种技术可以使 FFT 更快；但改进只有大约 20-40%。在其中一种方法中，当每个信号仅由四个点组成时，时域分解提前两个阶段停止。使用高度优化的代码直接跳转到频域，而不是计算最后两个阶段，使用四点正弦波和余弦波的简单性。

另一种流行的算法消除了与时域的虚部为零和频谱对称相关的浪费计算。换言之，修改 FFT 以计算实际 DFT，而不是复数 DFT。这些算法称为实数 FFT 和实数逆 FFT（或类似名称）。预计它们比传统的 FFT 例程快约 30%。表 12-6 和 12-7 显示了这些算法的程序。

使用真正的FFT有两个小缺点：

• 首先，代码的长度大约是原来的两倍。
• 其次，调试这些程序稍微困难一些，因为不能使用对称性来检查是否正确运行。这些算法强制时域的虚部为零，频域具有左右对称性。对于调试，请检查这些程序是否产生与传统 FFT 算法相同的输出。

图 12-10 和 12-11 说明了实际 FFT 的工作原理。在图12-10中，（a）和（b）显示了一个时域信号，该信号由实部中的脉冲和虚部中的所有零组成。图（c）和（d）显示了相应的频谱。频域的实部在样本 0 和样本 N/2 周围具有偶数对称性，而虚部在这些相同点周围具有奇数对称性。

现在考虑图 12-11，其中脉冲位于时域的虚部，实部全为零。频域中的对称性是相反的；实数部分是奇数，而虚数部分是偶数。

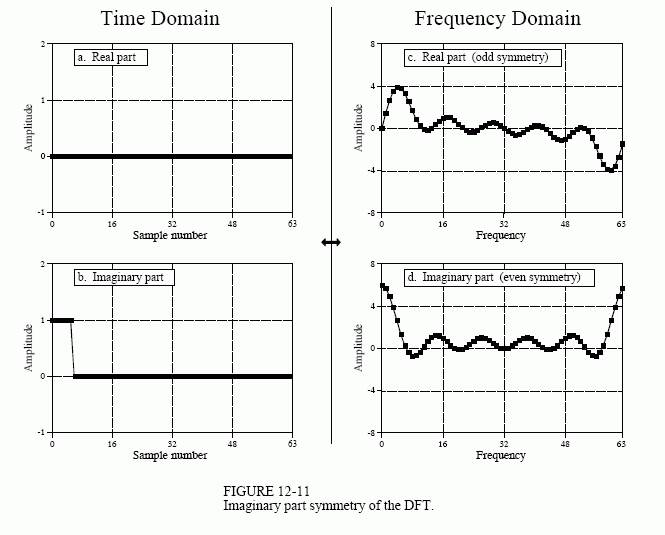
如果时域的两个部分都有信号怎么办？ 通过加性，频域是两个频谱的总和。关键要素是：由这两种对称性组成的频谱可以完美地分离成两个分量信号。其中一个信号放置在时域的实部，另一个信号放置在虚部。在计算复数DFT（当然是通过FFT）之后，使用偶数/奇数分解分离光谱。当需要通过两个或多个信号通过FFT时，该技术可将执行时间缩短约40%。

下一步是修改算法以更快地计算单个 DFT。通过使用隔行分解将输入信号分成两半。N/2 个偶数点被放置在时域信号的实部，而 N/2 个奇点被置于虚部。然后计算 N/2 点 FFT，所需时间约为 N 点 FFT 的一半。然后通过偶数/奇数分解分离产生的频域，从而产生两个交错时域信号的频谱。然后将这两个频谱组合成一个频谱，就像在FFT的最后一个合成阶段一样。

这篇关于信号系统之快速傅里叶变换的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---