本文主要是介绍国防科大、中大0706大气科学及南信大大物院初试复习宝典——第五章:大气热力学篇,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
零、前言
本人为24考研人,一开始想考中山大学,后来改为国防科技大学,最终总分390,因为一直有用博客做笔记的习惯,考后打算将考研期间的复习笔记无偿分享出来,因为之前在一些网站上买的资料太垃圾了,又贵又垃圾实在看不惯他们,还不如自己的笔记,买资料也建议看看有无直系学长总结的资料卖,就算要钱卖的也是干货和对学弟学妹的关心,我就很幸运遇到一个真心想帮学弟学妹在中大的学长
这个系列博客包含南信大大气物理学院,中山大学或国防科技大学0706大气科学研究生初试中超全知识点,三所学校所考内容参考书目相同,但考试题型不同,国防科技大学会考计算和推导,因此南信大、中大的考试内容是国防科大考试的子集,一篇顶三校考纲
各个知识点我会将重点标出以便大家复习,标了重点的一定要回参考书目中自己再弄懂一遍
文章内容大部分来自本人啃书得到,少部分来自购买资料,基本纯手敲
如果有疏漏和错误敬请在评论中指出,欢迎大家批评指正
一、热力学系统
- 气象上的热力学系统就是气象上热力学的研究对象,一般指空气微团
- 相对于气块的周围大气称为气块的环境,称为气层
1.1 气块
- 气块是宏观上体积非常小,微观上由大量空气分子组成
- 具有统计平均性和状态均衡性
- 气块与气层的相互作用通过做功,热传递和质量交换
1.2 三种系统
- 孤立系统:不交换能量,不交换质量,是一个与气层隔绝的系统
- 封闭系统:不交换质量,但是可以通过做功和热传导进行能量的交换
- 开放系统:既可以交换质量也可以交换能量
二、热力学过程
指气块由初始状态到终止状态的变化
2.1 四种过程
- 准静态过程:指一个系统在外界影响下经历的过程非常缓慢,在过程中任意时刻都是平衡态,即气块压强和气层压强始终相等
- 绝热过程:指气块和气层只通过做功的方式进行能量交换,没有热传导,绝热过程没有质量的交换
- 非绝热过程:气块和气层之间既通过做功产生能量交换,也通过热传导产生质量交换,非绝热过程可以有质量的交换,也可以没有质量的交换
- 可逆过程:过程的每一步向相反方向进行的时候都能回复原状,而且不引起外界任何变化,满足无摩擦,质量守恒,准静态的过程就是可逆过程,可逆过程时刻处于平衡态
三、热力学第一定律
热力学第一定律是能量转换与守恒定律
改变内能的两种方式:做功、热传导 改变内能的两种方式:做功、热传导 改变内能的两种方式:做功、热传导
3.1 基本公式
U − U 0 = W + Q U-U_0=W+Q U−U0=W+Q
- U − U 0 就是内能的改变量,是状态量 U-U_0就是内能的改变量,是状态量 U−U0就是内能的改变量,是状态量
- W表示系统与外界做功的交换,是过程量,W>0表示外界对系统做功
- Q表示系统与外界热量的交换,也是过程量,Q>0表示外界向系统输送热量
3.2 微分形式
d U = δ W + δ Q dU=\delta W+\delta Q dU=δW+δQ
之所以U用d,剩下两个用delta,是因为内能是状态量,做功和热传导是过程量
对于准静态系统,系统内部压强和外界压强始终相等,因此 p ˉ \bar p pˉ恒定,则dW可以写成 δ W = − p ˉ d V \delta W=-\bar pdV δW=−pˉdV
用压强乘体积的改变量表示外界对系统做功的大小,则微分形式可以表示成
d U = − p ˉ d V + δ Q dU=-\bar pdV+\delta Q dU=−pˉdV+δQ
3.3 比态量
由于大气的质量很难获取,因此常用比态量来表是上述方程,比态量就是强度量/质量
- 强度量常用的有内能U,热量Q,功W,熵S,焓H,自由能G和体积V,强度量是指没有方向的标量物理量,压强就不是强度量
- 而比态量就是强度量除以质量,一般用对应的小写字母表示,如比内能u=U/m、比热q=Q/m,比容 α = V / m = 1 / ρ \alpha=V/m=1/\rho α=V/m=1/ρ,比热q容易和比湿混淆,书写上仍用Q表示比热
- 将上式用比态量表示为
δ Q = m ( d u + p d α ) \delta Q=m(du+pd\alpha) δQ=m(du+pdα)
3.4 焓
焓H=U+pV,即内能和压能之和
- 比焓 h = H / m = u + p α h=H/m=u+p\alpha h=H/m=u+pα
- δ Q = d ( U + p V ) − V d p = d H − V d p \delta Q=d(U+pV)-Vdp=dH-Vdp δQ=d(U+pV)−Vdp=dH−Vdp,如果用比态量表示就是
δ Q = m ( d h − α d p ) \delta Q=m(dh-\alpha dp) δQ=m(dh−αdp) - 在等压过程中,焓的变化就是热量的变化
c p = δ Q d T = ( ∂ H ∂ T ) p c_p=\frac{\delta Q}{dT}=(\frac{\partial H}{\partial T})_p cp=dTδQ=(∂T∂H)p
3.5 比热
实验表明,一定质量的系统吸收或放出的热量与温度变化有密切关系
δ Q = m c d T , c 就为系统的比热容 \delta Q=mcdT,c就为系统的比热容 δQ=mcdT,c就为系统的比热容
- 在等压过程和等容过程中的比热称为定压比热 c p c_p cp和定容比热 c v c_v cv
- 对于等容过程, d α = 0 d\alpha=0 dα=0,第一定律就化为 d Q = d U = m d u = m c v d T dQ=dU=mdu=mc_vdT dQ=dU=mdu=mcvdT;即 d u = c v d T du=c_vdT du=cvdT
- 对于等压过程, d p = 0 dp=0 dp=0,第一定律化为 d Q = d H = m d h = m c p d T dQ=dH=mdh=mc_pdT dQ=dH=mdh=mcpdT,即 d h = c p d T dh=c_pdT dh=cpdT
3.6 结合状态方程
由 h = u + p α ; p α = R T 连立得 由h=u+p\alpha;p\alpha=RT连立得 由h=u+pα;pα=RT连立得
d h = d u + R d T = c v d T + R d T = c p d T ,可见 dh=du+RdT=c_vdT+RdT=c_pdT,可见 dh=du+RdT=cvdT+RdT=cpdT,可见
c p = c v + R c_p=c_v+R cp=cv+R
因此第一定理还可以写成(气象上常用的热力学方程)
δ Q = m ( c v d T + p d α ) = m ( c p d T − α d p ) \delta Q=m(c_vdT+pd\alpha)=m(c_pdT-\alpha dp) δQ=m(cvdT+pdα)=m(cpdT−αdp)
四、热力学第二定律
第二定律阐述的是系统状态变化的方向以及系统达到平衡或处于平衡的必要条件,其进行的限度是系统的熵达到最大
另一种表述:从平衡态开始而终于另一个平衡态的过程,将朝着系统与外界总熵增加的方向进行
4.1 公式表达
S − S 0 ≥ ∫ ω 0 ω δ Q T ˉ S-S_0 \geq \int_{\omega_0}^\omega \frac{\delta Q}{\bar T} S−S0≥∫ω0ωTˉδQ
- S − S 0 S-S_0 S−S0表示终态的熵-初态的熵, ω 表示状态 \omega表示状态 ω表示状态, T ˉ \bar T Tˉ表示环境温度
- 熵是状态量,因此与积分路径无关
- 在可逆过程中,上式取等号,同时可逆过程中时刻处于平衡态,因此温度等于环境温度, T = T ˉ , T=\bar T, T=Tˉ,取微分就为 d S = δ Q T dS=\frac{\delta Q}{T} dS=TδQ
- 定义系统熵:熵在可逆过程中的变化等于系统所吸收的热量与热源的绝对温度之比
- 因此对于可逆绝热过程, δ Q = 0 \delta Q=0 δQ=0,为等熵过程
- 但对于不可逆绝热过程 d S > δ Q / T > 0 dS>\delta Q/T>0 dS>δQ/T>0,为熵增过程,因此在不可逆过程中,系统总熵将增加
4.2 在第一定律中的表达
- 对于封闭系的可逆过程中,热量的变化 δ Q = T d S \delta Q=TdS δQ=TdS,第一定律则可以写成
d U = T d S − p d V dU=TdS-pdV dU=TdS−pdV
或 d H = T d S + V d p 或dH=TdS+Vdp 或dH=TdS+Vdp
4.3 自由焓(吉布斯自由能)
定义G=H-TS=U+pV-TS
取微分 d G = d U + p d V + V d p − T d S − S d T 取微分 dG=dU+pdV+Vdp-TdS-SdT 取微分dG=dU+pdV+Vdp−TdS−SdT
其中 d U + p d V − T d S < = 0 其中dU+pdV-TdS<=0 其中dU+pdV−TdS<=0
因此有 d G < = V d p − S d T 因此有dG<=Vdp-SdT 因此有dG<=Vdp−SdT
- 封闭系统在外界恒温恒压,只做体胀功,以及系统的初态、终态与外界温度和气压相等时,自由焓永不增加;对于可逆过程 Δ G = 0 \Delta G=0 ΔG=0,对不可逆过程 Δ G < 0 \Delta G<0 ΔG<0
4.4 小结
T d s = d u + p d α Tds=du+pd\alpha Tds=du+pdα
T d s = d h − α d p Tds=dh-\alpha dp Tds=dh−αdp
S d T = V d p − d G SdT=Vdp-dG SdT=Vdp−dG
五、热力学函数(麦克斯韦关系式)
记忆方法
- SUV,哈佛(HF),排骨汤(PGT)排列之后
- 同一行或同一列的就是写成微分的两个微分变量
- 从左到右遇到V或者T要加负号,第二列有dF=-SdT-pdV
- p与V对应,T与S对应
六、未饱和湿空气系统
- 未饱和湿空气:实际水汽压小于该系统的温度所对应的饱和水汽压,系统中无液态水和冰的存在
- 可以看作是理想气体
- 未饱和湿空气和干空气用热力学第一定律表示就为
对干空气 δ Q = m ( c d v d T + R d T d p p ) 对干空气\delta Q=m(c_{dv}dT+R_d T\frac{dp}{p}) 对干空气δQ=m(cdvdT+RdTpdp)
对未饱和湿空气 δ Q = m ( c m v d T + R m T d p p ) 对未饱和湿空气\delta Q=m(c_{mv}dT+R_m T\frac{dp}{p}) 对未饱和湿空气δQ=m(cmvdT+RmTpdp) - R m ≈ R d ( 1 + 0.608 q ) , R m R_m\approx R_d(1+0.608q),R_m Rm≈Rd(1+0.608q),Rm为未饱和湿空气的比气体常数
- c p m ≈ c p d ( 1 + 0.84 q ) c_{pm}\approx c_{pd}(1+0.84q) cpm≈cpd(1+0.84q),两者相差很小,实际当中将未饱和湿空气当作干空气处理也不会有太大误差
七、克拉珀龙——克劳修斯方程
- 相变平衡:水物质汽液两相平衡共存于系统且两相的水物质的质量保持不变,称为相变平衡;此时水汽压称为饱和水汽压;两相的温度,压强,1mol物质的吉布斯函数(化学势)相等且不发生变化
- 克拉珀龙——克劳修斯方程描述的就是相平衡时饱和水汽压随温度变化的关系式
7.1 相变潜热
定义相变潜热 l l l 为单位质量的1相态转变为同温度的2相态时,从外界吸收的热量
- 假设相变是在等温(即等压)条件下进行的,因此热量的改变量就是焓的改变量
l 1 , 2 = h 1 − h 2 l_{1,2}=h_1-h_2 l1,2=h1−h2
7.2 推导
- 对于可逆相变而言,有自由焓不变,即 Δ g = g 2 − g 1 = 0 \Delta g=g2-g1=0 Δg=g2−g1=0
- 即 − s 1 d T + α 1 d p = − s 2 d T + α 2 d p -s_1dT+\alpha_1 dp=-s_2 dT+\alpha_2 dp −s1dT+α1dp=−s2dT+α2dp
- 整理得到
d p d T = s 2 − s 1 α 2 − α 1 = h 2 − h 1 T ( α 2 − α 1 ) = l T ( α 2 − α 1 ) \frac{dp}{dT}=\frac{s_2-s_1}{\alpha_2 - \alpha_1}=\frac{h_2-h_1}{T(\alpha_2 - \alpha_1)}=\frac{l}{T(\alpha_2 - \alpha_1)} dTdp=α2−α1s2−s1=T(α2−α1)h2−h1=T(α2−α1)l - 方程中的p指的是平衡时的汽相压强,一般也可以用饱和水汽压表示
- 该方程揭示了两相平衡时温度,压强,相变潜热之间的关系
7.3 应用于水和汽两相的近似公式(记忆)
d p s d T = l v T ( α v s − α l s ) \frac{dp_s}{dT}=\frac{l_v}{T(\alpha_{vs} - \alpha_{ls})} dTdps=T(αvs−αls)lv
- 这个表示的就是从汽相通过相变转化为液相时候的方程
- 两相平衡时汽相的压强就是饱和水汽压E
- 汽相的比容远大于液相的,因此 ( α v s − α l s ) ≈ a v s (\alpha_{vs} - \alpha_{ls})\approx a_{vs} (αvs−αls)≈avs,并用 α v s = R v T E \alpha_{vs}=\frac{R_v T}{E} αvs=ERvT
- 因此方程可以近似为
d e s d T = e s l v R v T 2 ; l v 为蒸发潜热 \frac{de_s}{dT}=\frac{e_sl_v}{R_vT^2};l_v为蒸发潜热 dTdes=RvT2eslv;lv为蒸发潜热
八、干绝热方程(重中之重)
干绝热过程:在垂直运动过程中,气块所含的水汽始终未达到饱和,没有发生相变的绝热过程,满足下述三个条件,干绝热方程是可逆过程
8.1 气块垂直运动的三个假定条件
- 绝热条件:垂直运动中气块与气层始终不发生热量交换,因为气块在垂直运动中垂直速度较大,来不及和外界发生热量交换,同时短时间内由于辐射,湍流和分子传导等作用与外界交换的热量远小于其自身由于膨胀或压缩与外界交换的热量
- 准静态条件:气块压强与气层压强始终相等
- 静力平衡条件:气块做垂直运动时,气层是静止的
这样气块的气压随高度的变化和气层气压随高度的变化是一致的
8.2 方程本身
-
由于绝热过程,第一定律写为
0 = m ( c p m d T − R m T d p p ) 0=m(c_{pm}dT-R_mT\frac{dp}{p}) 0=m(cpmdT−RmTpdp)
积分后写为 T T 0 = ( p p 0 ) R m / c p m 积分后写为\frac{T}{T_0}=(\frac{p}{p_0})^{R_m/c_{pm}} 积分后写为T0T=(p0p)Rm/cpm -
可见干绝热过程中,气块的温度仅取决于气压
-
κ = R m c p m ≈ κ d = 0.286 \kappa =\frac{R_m}{c_{pm}}\approx\kappa_d=0.286 κ=cpmRm≈κd=0.286
九、位温(重中之重)
气块经过干绝热过程移动到1000hPa时对应的温度
由干绝热方程可得
θ m = T ( 1000 p ) R m / c p m \theta_m=T(\frac{1000}{p})^{R_m/c_{pm}} θm=T(p1000)Rm/cpm
可见位温由气块所在的位置和温度共同决定
9.1 干绝热过程位温守恒推导
两端取对数之后进行全微分,变形后得到
T c p m d θ m θ m = c p m d T − R m T d p p Tc_{pm}\frac{d\theta_m}{\theta_m}=c_{pm}dT-R_mT\frac{dp}{p} Tcpmθmdθm=cpmdT−RmTpdp
左右两边同乘质量m
m T c p m d θ m θ m = m ( c p m d T − R m T p d p ) = δ Q mTc_{pm}\frac{d\theta_m}{\theta_m}=m(c_{pm}dT-\frac{R_mT}{p}dp)=\delta Q mTcpmθmdθm=m(cpmdT−pRmTdp)=δQ
也可以写成
d s = c p m d θ m θ m ds=c_{pm}\frac{d\theta_m}{\theta_m} ds=cpmθmdθm
可见,位温的改变其实是由于热量的变化造成的,气块吸热其位温增高,放出时位温降低,而绝热过程中热量不变,因此位温守恒,同时比熵也是相等的,干绝热过程也称为等熵过程
9.2 位温的垂直变化
对热力学方程两端取对数之后对z求偏导
∂ θ ∂ z θ = ∂ T ∂ z T − R c p ∂ p ∂ z = − γ T + g c p 1 T \frac{\partial \theta}{\partial z \theta}=\frac{\partial T}{\partial z T}-\frac{R}{c_p}\frac{\partial p}{\partial z}=-\frac{\gamma}{T}+\frac{g}{c_p}\frac{1}{T} ∂zθ∂θ=∂zT∂T−cpR∂z∂p=−Tγ+cpgT1
其中 g c p \frac{g}{c_p} cpg就是干绝热递减率 γ v \gamma_v γv; γ \gamma γ就是气块温度递减率
∂ θ ∂ z = θ T ( γ v − γ ) ≈ θ T ( γ d − γ ) \frac{\partial \theta}{\partial z}=\frac{\theta}{T}(\gamma_v - \gamma)\approx \frac{\theta}{T}(\gamma_d - \gamma) ∂z∂θ=Tθ(γv−γ)≈Tθ(γd−γ)
可见当气层温度递减率=干绝热递减率时,位温不随高度变化;一般状况下大气垂直递减率小于干绝热递减率,因此一般而言,位温随高度是增加的
十、干绝热直减率
未饱和湿空气在可逆干绝热过程中温度随高度上升的降低率称为干绝热直减率 γ d = − d T d z \gamma_d=-\frac{dT}{dz} γd=−dzdT
10.1 推导
由热力学方程
0 = m ( c p m d T − R m T d p p ) 即 0=m(c_{pm}dT-R_mT\frac{dp}{p})即 0=m(cpmdT−RmTpdp)即
以及静力平衡方程,以及准静态假设条件
d p d z = d p ˉ d z = − ρ ˉ g = − p R T ˉ g \frac{dp}{dz}=\frac{d\bar p}{dz}=-\bar \rho g=-\frac{p}{R\bar T}g dzdp=dzdpˉ=−ρˉg=−RTˉpg
联立得(气块的气压和温度与气层近似看作相等)
γ d = − d T d z ≈ g c p m ≈ 9.8 ( k / k m ) \gamma_d=-\frac{dT}{dz}\approx \frac{g}{c_{pm}}\approx9.8 (k/km) γd=−dzdT≈cpmg≈9.8(k/km)
其中R是湿空气的比气体常数,cp是湿空气的比热,只是因为实际大气中q太小了,近似用干空气R与cp就足够精确了
10.2 露点在干绝热过程中的变化规律
由于在干绝热上升中,没有液态水凝结出来,因此比湿不变 q = 0.622 e p − 0.378 e ≈ 0.622 e p q=0.622\frac{e}{p-0.378e}\approx0.622 \frac{e}{p} q=0.622p−0.378ee≈0.622pe
两端取对数求积分得到
d l n q ≈ d l n e − d l n p = 0 dlnq\approx dlne-dlnp=0 dlnq≈dlne−dlnp=0
可见e和p的变化是相等的,即水汽压是随气压变化的,随着气压的降低水汽压也是降低的,水汽压和露点温度也是挂钩的,因此露点温度和气压也是相关的,气压越低,水汽压越小,温度越低,露点温度也会降低
由于水汽压e和气压p的变化是相同的,因此克劳修斯方程可以写为
d e d T d = l v e R v T d 2 与 d l n e = d l n p 连立得到 \frac{de}{dT_d}=\frac{l_v e}{R_vTd^2}与dlne=dlnp连立得到 dTdde=RvTd2lve与dlne=dlnp连立得到
β d = d T d d z = R v T d 2 l v p d p d z = − g T d 2 R v R d T ˉ v l v \beta_d=\frac{dT_d}{dz}=\frac{R_vT_d^2}{l_vp}\frac{dp}{dz}=-\frac{gT_d^2R_v}{R_d \bar T_v l_v} βd=dzdTd=lvpRvTd2dzdp=−RdTˉvlvgTd2Rv
若取 T d T ˉ v ≈ 1 \frac{T_d}{\bar T_v}\approx1 TˉvTd≈1,则 β d ≈ 1.7 k / k m \beta_d \approx 1.7k/km βd≈1.7k/km
10.3 抬升凝结高度
未饱和湿空气在干绝热上升中,温度递减率比露点递减率快,在上升到一定高度后,会出现温度和露点相等的时候,此时气块达到饱和,此时的高度称为抬升凝结高度
T 0 − γ d ( z c − z 0 ) = T d 0 − β d ( z c − z 0 ) T_0-\gamma_d(z_c-z_0)=T_{d0}-\beta_d(z_c-z_0) T0−γd(zc−z0)=Td0−βd(zc−z0)
这个式子表明,气块上升到抬升凝结高度过程中,气块温度和露点温度降低直到两者相等,解出来就为
z c = z 0 + T 0 − T d 0 γ d − β d ≈ z 0 + 123 ( T d − T d 0 ) z_c=z_0+\frac{T_0-T_{d0}}{\gamma_d - \beta_d}\approx z_0+123(T_d-T_{d0}) zc=z0+γd−βdT0−Td0≈z0+123(Td−Td0)
抬升凝结高度由初始时候的温度露点差决定,气块越接近饱和抬升凝结高度就越低
因此如果湿度大,温度露点查就小,更快达到抬升凝结高度,从而容易达到自由对流高度,CIN值就小
十一、可逆和不可逆湿绝热过程(重点)
可逆湿绝热过程:当水汽开始凝结并释放潜热时,若==凝结物保留在气块内,且当下沉增温时这些凝结物又蒸发,==所耗的潜热和原来释放的潜热相等,沿逆过程能回到原来状态的过程称为可逆湿绝热过程,可逆湿绝热过程是等熵过程
不可逆湿绝热过程:如果凝结物全部脱离气块,下沉时则没有可蒸发的水汽,气块处于未饱和状态,即下沉过程是干绝热过程,下沉到原来位置时温度就会比之前高,是不可逆的,由于凝结物要带走热量,因此不是严格的绝热过程,也称假绝热过程
这两种情况都是极端情况,实际大气的绝热过程介于两者之间
十二、湿绝热方程
相比干绝热方程,多了潜热项
c p d d T − α d p + L v d r s ≈ 0 c_{pd}dT-\alpha dp+L_v dr_s \approx 0 cpddT−αdp+Lvdrs≈0
Lv为相变潜热,dr为饱和水汽混合比的变化,可以理解为水汽混合比发生变化就要释放潜热或者吸收热量,导致热量的变化
- 具体来讲,混合比减少,说明水汽减少,液态水增加,有潜热释放,移到右侧就是大于0的,就等于向系统中提供了热量的效果
十三、假相当位温
在湿绝热过程中,如果凝集物脱离气块,但是潜热仍然保留在气块中,那么当它再按干绝热过程下沉到1000hP,其温度是比没有发生凝结时高的,因此在湿绝热过程中,位温不守恒
考虑了水汽作用后的位温,是气块经过假绝热过程上升直到水汽全部凝结脱落之后下降到1000hPa的温度
饱和湿气块的假相当位温公式:只要确定了p,T就可以确定其假相当位温
θ s e = θ d e x p ( r s l v c p d T ) \theta_{se}=\theta_d exp(\frac{r_sl_v}{c_{pd}T}) θse=θdexp(cpdTrslv)
对于未饱和湿空气而言,常用气块在凝结高度的假相当位温表示其假相当位温,是一个以(p,T, r 0 r_0 r0)为参数的态函数
θ s e c = θ d e x p ( r 0 l v c c p d T c ) \theta_{sec}=\theta_dexp(\frac{r_0 l_{vc}}{c_{pd}T_c}) θsec=θdexp(cpdTcr0lvc)
-
r为混合比
-
严格地来说,饱和式空气的假相当位温是随温度的减小而增大的,但是增大的量级很小,一般可以忽略不计,于是可逆湿绝热过程和假绝热过程近似是等假相当位温过程
-
而对于未饱和空气而言,在达到抬升凝结高度之前位温守恒,达到之后假相当位温守恒,因此对于未饱和空气而言假相当位温也是守恒,综上假相当位温在干,湿绝热过程中均是守恒的
-
当气块上升到水汽全部凝结出来,此时的假相当位温=位温
十四、假相当温度
位温和温度的转换公式,由位温公式
θ m = T ( 1000 p ) R m / c p m \theta_m=T(\frac{1000}{p})^{R_m/c_{pm}} θm=T(p1000)Rm/cpm移项之后得到
T = θ m ( p 1000 ) R m / c p m T=\theta_m(\frac{p}{1000})^{R_m/c_{pm}} T=θm(1000p)Rm/cpm
因此假相当温度就是用这个公式将假相当位温转换一下
T s e = θ s e ( p 1000 ) R m / c p m T_{se}=\theta_{se}(\frac{p}{1000})^{R_m/c_{pm}} Tse=θse(1000p)Rm/cpm
十五、湿绝热温度直减率
γ m = g c p d + l v c p d d r s d z = γ d + l v c p d d r s d z \gamma_m = \frac{g}{c_{pd}}+\frac{l_v}{c_{pd}}\frac{dr_s}{dz}=\gamma_d+\frac{l_v}{c_{pd}}\frac{dr_s}{dz} γm=cpdg+cpdlvdzdrs=γd+cpdlvdzdrs
当气块上升时,随高度增加水汽凝结,混合比减少, d r s d z < 0 \frac{dr_s}{dz}<0 dzdrs<0,当下沉的时候,随高度降低气温增加水蒸发,混合比增加,但是下沉是吸收潜热,L<0,整体还是会比因此不管上升还是下沉,湿绝热递减率都比干绝热递减率小
物理原因就是饱和湿空气上升的时候会水凝结,凝结释放潜热,起到补偿增温作用,温度递减率就会低,下沉的时候相反,水的蒸发需要吸收潜热,使温度递减率也会低
十六、焚风
- 气流经过山脉时被迫抬升,如果抬升凝结高度低于山高,则达到山顶之前就会有凝结物脱离气流
- 当气流过山后,由于没有或很少凝结物供蒸发,按干绝热递减率下沉
- 导致山后温度比山前同高度的温度高很多,湿度也小很多
十七、艾玛图(温度对数压力图——重中之重)
17.1 坐标
- 横坐标是线性坐标T
- 纵坐标是压强的对数坐标, y = l n 1000 p y=ln\frac{1000}{p} y=lnp1000
- 艾玛图上围成的面积就是循环过程中单位质量气块做的功
17.2 获取信息(重要,但好像不太好考)
- 饱和比湿:饱和比湿线上的数值就是饱和比湿
- 饱和水汽压:由于 q s ≈ 622 E ( T ) p q_s \approx 622\frac{E(T)}{p} qs≈622pE(T),如果p取622,就数值上水汽压就等于饱和水汽压,因此根据给定的温度找到等温线与622hPa的交点,读出该点的饱和比湿 q s q_s qs就是数值上的饱和水汽压E
- 假相当位温:气块上升到水汽全部凝结出来(先沿干绝热线上升到抬升凝结高度,之后沿湿绝热先上升直到水汽全部凝结),此时的假相当位温=位温,再沿干绝热线下降到1000hPa高度,此时的温度即假相当位温
- 假湿球位温 θ s w \theta_{sw} θsw:沿干绝热上升到凝结高度,再按湿绝热线下降到1000hPa高度对应的温度
- 假湿球温度 T s w T_{sw} Tsw:沿干绝热上升到凝结高度,再按湿绝热线下降到原先高度对应的温度
- 层结曲线:根据探空记录将各高度上的气压和温度(和露点温度)绘制在p,t图上
- 抬升凝结高度:初始点温度沿干绝热线上升;初始点露点沿等饱和比湿线上升,两者交点就是抬升凝结高度
- 对流凝结高度:下层为超绝热层,此时抬升凝结高度=对流凝结高度=自由对流高度
- 自由对流高度:正负面积的交点
- 热雷雨的预报:首先根据清晨的大气层结曲线确定当时的抬升凝结高度是多少,之后在抬升凝结高度做干绝热线,与地面相交的温度就是当天如果要发生热雷雨需要达到的地面最大气温
- 状态曲线:将绝热上升的空气快在不同高度的温度点绘制在图上,具体方式:绝热上升的路径就是到达抬升凝结高度之前是沿干绝热线,之后沿湿绝热线
十八、绝热混合
18.1 水平绝热混合
简化的等压绝热混合温度的计算式
T ≈ m 1 T 1 + m 2 T 2 m T\approx \frac{m_1T_1+m_2T_2}{m} T≈mm1T1+m2T2
对水汽压和位温也有同样形式的质量加权形式的混合后表达式
因此两股未饱和的空气混合后有可能会发生凝结
喷气飞机的尾流和开水壶喷出的雾气就是典型例子
18.2 垂直绝热混合
- 首先将两气块通过绝热膨胀或冷却压缩移到同一参考高度,该过程中位温和比湿守恒
- 之后在该高度上进行水平混合,同样是按质量加权混合,得到新的混合后的位温
- 之后用位温的逆公式,让气块绝热回到原来的高度
T = θ ( p 1000 ) κ T=\theta(\frac{p}{1000})^\kappa T=θ(1000p)κ,就可以得到垂直混合之后的温度
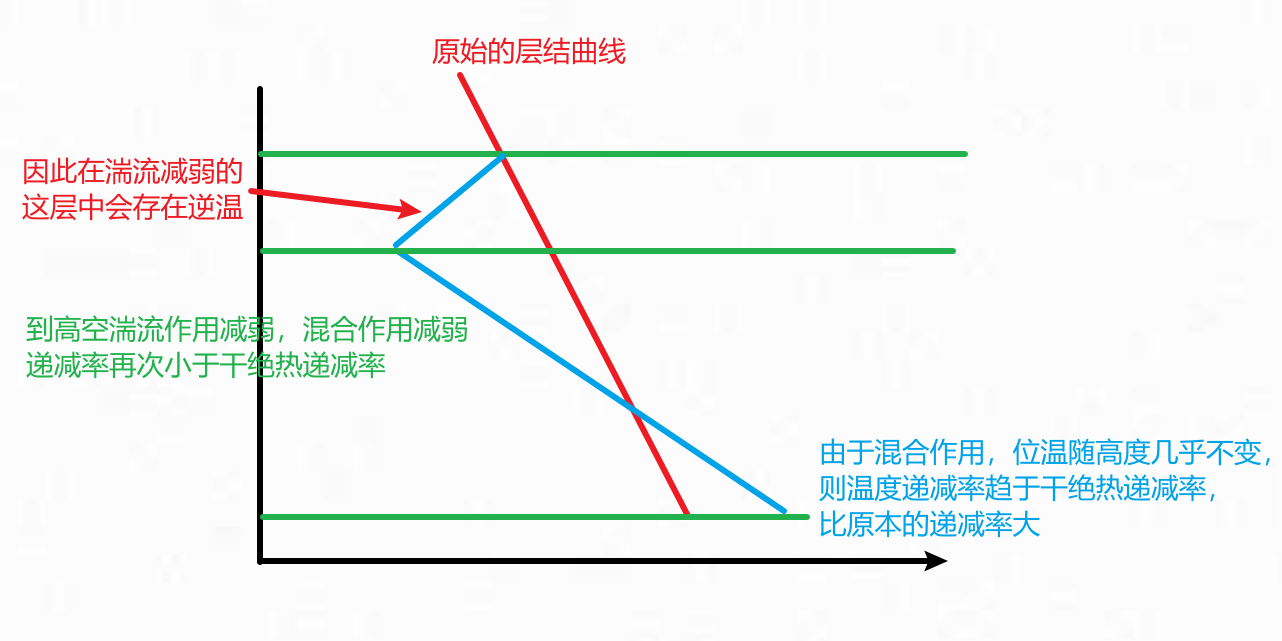
十九、湍流混合(湍流逆温——重要)
- 由于湍流的混合作用,会使气层内空气充分混合均匀,湿度,温度都将趋于一致
- 由上文中位温随高度的关系可知,当湍流混合导致位温垂直方向不变的时候,有气层温度递减率=干绝热递减率
- 因此在混合层(湍流作用较强),由于湍流作用会让气块趋于沿干绝热递减率上升
- 直到高空湍流的作用减弱的地方,空气不再混合得均匀,以至于到一定高度会恢复气层递减率低于干绝热递减率
- 那在这个湍流减弱的地方就会出现逆温层
二十、温湿参量(名词解释)
20.1 相当温度( T e T_e Te)/相当位温( θ e \theta_{e} θe)
系统经等压绝热蒸发过程成为湿空气之前,绝对干燥的空气具有的温度,因为蒸发吸热,因此在系统蒸发前绝对干燥的空气是等压绝热蒸发过程中可能有过的最高温度
相当位温就是将相当温度对应的位温
20.2 湿球温度( T w T_{w} Tw)
系统内的液态水蒸发使空气降温达到饱和时空气所具有的温度,是这个过程中的最低温度
- 实际中,用一个玻璃温度表球部用吸饱水的纱布包裹成为湿球,当周围空气未饱和时,纱布上的水分必然会蒸发并使周围空气降温;而达到饱和的时候达到定常,此时的温度即湿球温度
20.3 假湿球温度( T s w T_{sw} Tsw)和假湿球位温( θ s w \theta_{sw} θsw)
空气由原来的状态A沿干绝热线上升到抬升凝结高度之后,沿湿绝热线下降到原来的高度即假湿球温度,用 T s w T_{sw} Tsw表示
假湿球温度总是小于湿球温度
假湿球位温就是空气由原来的状态A沿干绝热线上升到抬升凝结高度之后,沿湿绝热线下降到1000hPa
假湿球位温在干绝热和湿绝热过程中都是保守的
20.4 假相当温度( T s e T_{se} Tse)和假相当位温( θ s e \theta_{se} θse)
气块先沿干绝热线上升到抬升凝结高度,之后沿湿绝热线上直到水汽耗尽,之后沿干绝热线下降到原始高度/1000hPa高度时对应的温度就是假相当温度/假相当位温
20.5 小结
在几个温湿参量当中,假相当位温和假湿球温度对于干绝热和湿绝热过程都是保守的
在分析锋面,气团,焚风的时候常用这两个温湿参量
抬升凝结高度处的温度<原来高度上的露点温度 < 假湿球温度 < 湿球温度 < 温度 < 虚温 < 相当温度 < 假相当温度
假湿球位温 < 位温 < 虚位温 < 假相当位温
由艾玛图可以很容易得知
二十一、大气稳定度(气块法——重要)
当物体处于静力平衡时,其平衡性质是不一样的,给一个外力使其偏离平衡位置后的运动趋势,可能维持平衡,可能加速偏离平衡位置,或在新的位置上静止
层结大气所具有的这种影响垂直运动的特性称为大气的静力稳定度
如果有个气块受力后产生垂直运动,撤去外力后,可能出现这几种类型的运动情况:
- 气块减速,回到原位——稳定
- 气块往原方向加速运动——不稳定
- 在新的位置静止——中性
大气稳定度是== 表示大气层结对气块能否产生对流的一种潜力的度量==
21.1 气块法的假设(重要)
- 假设气块做垂直运动时,周围空气始终处于静力平衡状态
- 气块与周围环境无混合
- 气块与周围环境的气压时刻相等
- 其假设就是气块法的局限性所在
21.2 垂直加速度判据(重要)
从气块的垂直加速度入手,垂直加速度 = 垂直方向受力 / 质量
F = − ∂ p ∂ z d z − m g F=-\frac{\partial p}{\partial z}dz-mg F=−∂z∂pdz−mg
同时除以 m = ρ d z m=\rho dz m=ρdz(因为是单位面积,因此体积就是1dz)
d w d z = − 1 ρ ∂ p ∂ z − g \frac{dw}{dz}=-\frac{1}{\rho}\frac{\partial p}{\partial z}-g dzdw=−ρ1∂z∂p−g
而 ∂ p ∂ t = − ρ e g \frac{\partial p}{\partial t}=-\rho_e g ∂t∂p=−ρeg即环境温度大气的密度
d w d t = ρ e ρ g − g = ρ e − ρ ρ g \frac{dw}{dt}=\frac{\rho_e}{\rho}g-g=\frac{\rho_e - \rho}{\rho}g dtdw=ρρeg−g=ρρe−ρg
由此可见,气块和环境的密度差决定了气块的加速度
由准静力条件得
ρ e ρ = T v T v e ≈ T T e \frac{\rho_e}{\rho}=\frac{T_v}{T_{ve}}\approx \frac{T}{T_{e}} ρρe=TveTv≈TeT
d w d t = T − T e T e g \frac{dw}{dt}=\frac{T - T_e}{T_e}g dtdw=TeT−Teg
因此用气块和环境的温差也可以判断加速度方向
注意密度之比和温度之比是反比,密度是环境-气块,温度是气块-环境
21.3 用减温率表示的垂直加速度(重要)
气块减温率用 γ \gamma γ表示,气层减温率用 Γ \Gamma Γ表示
则经过一小段位移之后, T 0 T_0 T0为平衡时温度
T = T 0 − γ d z ; T e = T 0 − Γ d z T=T_0-\gamma dz;T_e=T_0-\Gamma dz T=T0−γdz;Te=T0−Γdz
将上式带入后得到
d w d t = Γ − γ T e g d z \frac{dw}{dt}=\frac{\Gamma - \gamma}{T_e}gdz dtdw=TeΓ−γgdz
也就是用环境和气块温度递减率之差也可以表征气块加速度
如果气层温度递减率更大,说明气块温度高,是不稳定的
对于含有液态水的饱和气层,则用 γ m 与 γ \gamma_m与\gamma γm与γ进行比较
21.4 用位温表达的稳定度(重要)
将气层的位温表达式等式两边取对数之后对z进行微分
1 θ ˉ ∂ θ ˉ ∂ z = 1 T ˉ ∂ T ˉ ∂ z − R d p ˉ c p d ∂ p ∂ z = − 1 T ˉ γ + g c p d 1 T ˉ \frac{1}{\bar \theta}\frac{\partial \bar \theta}{\partial z}=\frac{1}{\bar T}\frac{\partial \bar T}{\partial z}-\frac{R_d}{\bar p c_{pd}}\frac{\partial p}{\partial z}=-\frac{1}{\bar T}\gamma+\frac{g}{c_{pd}}\frac{1}{\bar T} θˉ1∂z∂θˉ=Tˉ1∂z∂Tˉ−pˉcpdRd∂z∂p=−Tˉ1γ+cpdgTˉ1
从而得到
∂ θ ˉ ∂ z = θ ˉ T ˉ ( γ d − γ ) \frac{\partial \bar \theta}{\partial z}=\frac{\bar \theta}{\bar T}(\gamma_d - \gamma) ∂z∂θˉ=Tˉθˉ(γd−γ)
可见当干绝热递减率大于气层的递减率时,是稳定的,环境位温随高度升高
如下结论:
- 气层的位温随高度变化情况与 γ d − γ \gamma_d-\gamma γd−γ相同
- 气层位温随高度升高——稳定
- 气层位温随高度降低——不稳定
- 对于含有液态水的饱和气层,则用假相当位温随高度的变化进行比较
21.5 饱和但不含有液态水的气层稳定度
- 饱和但不含有液态水的气层上升时是沿湿绝热线,下沉时则是沿干绝热线,因此稳定度要视扰动方向而定
21.6 绝对、条件、绝对不(重要,理解)
- 绝对不稳定 γ > γ d \gamma > \gamma_d γ>γd
- 绝对稳定 γ < γ m \gamma < \gamma_m γ<γm
- 条件稳定 γ m < γ < γ d \gamma_m < \gamma < \gamma_d γm<γ<γd
- 如果含有液态水,上升下沉都按湿绝热,那就是不稳定的
- 如果饱和但是不含液态水,上升按湿绝热,是不稳定的,下沉按干绝热,是稳定的
- 如果是未饱和,那就是稳定的
- 条件稳定 γ = γ d \gamma = \gamma_d γ=γd:
- 如果含有液态水,是不稳定的
- 如果饱和但不含液态水,上升不稳定,下沉中性
- 如果未饱和,则是中性的
- 条件稳定 γ = γ m \gamma=\gamma_m γ=γm:
- 如果含有液态水,是中性的
- 如果饱和但不含有液态水,上升中性,下沉稳定
- 如果未饱和则为稳定
二十二、气层不稳定能量
∫ z 0 z d w d t d z = ∫ z 0 z ( T v − T ˉ v T ˉ v ) g d z \int_{z_0}^z\frac{dw}{dt}dz=\int_{z_0}^z(\frac{T_v-\bar T_v}{\bar T_v})gdz ∫z0zdtdwdz=∫z0z(TˉvTv−Tˉv)gdz
∫ z 0 z d w d t d z = ∫ z 0 z d w d t w d t = 1 2 ( w 2 − w 0 2 ) = ∫ z 0 z ( T v − T ˉ v T ˉ v ) g d z \int_{z_0}^z\frac{dw}{dt}dz=\int_{z_0}^z\frac{dw}{dt}wdt=\frac{1}{2}(w^2-w_0^2)=\int_{z_0}^z(\frac{T_v-\bar T_v}{\bar T_v})gdz ∫z0zdtdwdz=∫z0zdtdwwdt=21(w2−w02)=∫z0z(TˉvTv−Tˉv)gdz
左边是动能增量,右边是做的功;可见,浮力和重力合力做的功,从一个高度到另一个高度能做这么多功,根据功与能量的关系,说明储存了这么多的能量
- 如果 ∫ z 0 z ( T v − T ˉ v T ˉ v ) g d z \int_{z_0}^z(\frac{T_v-\bar T_v}{\bar T_v})gdz ∫z0z(TˉvTv−Tˉv)gdz>0,则表示气层对气块做正功,称气块具有不稳定能量
- 反之气层对气块是稳定的,称气层具有负不稳定能量
22.1 在艾玛图上的分析
∫ z 0 z ( T v − T ˉ v T ˉ v ) g d z = R d ∫ p 0 p ( T v − T ˉ ) v d ( − l n p ) = R d ∫ p 0 p ( T v − T ˉ ) v d ( l n 1000 p ) \int_{z_0}^z(\frac{T_v-\bar T_v}{\bar T_v})gdz=R_d\int_{p_0}^p(T_v-\bar T)_v d(-lnp)=R_d\int_{p_0}^p(T_v-\bar T)_v d(ln\frac{1000}{p}) ∫z0z(TˉvTv−Tˉv)gdz=Rd∫p0p(Tv−Tˉ)vd(−lnp)=Rd∫p0p(Tv−Tˉ)vd(lnp1000)
其中 l n 1000 p ln\frac{1000}{p} lnp1000为艾玛图的纵坐标
于是在艾玛图上表现出来的就是不稳定能量与状态曲线和层结曲线围成的面积成正比,比例系数为 R d R_d Rd
- 绝对稳定型:气块温度总是小于气层温度,因此一直都是负面积,
- 绝对不稳定型:气块温度总是大于气层温度,不稳定能量面积为正,只要受到微小扰动,气层就会释放不稳定能量,转换为气块上升的动能
- 潜在不稳定型:存在一个交点,交点下方是负面积,上方是正面积,这个交点就是自由对流高度LFC;在该高度一下气块只能在外力的作用下强迫抬升,超过后就可以获得加速度自由上升;但之后如果状态曲线和层结曲线还有交点,又会出现负能量,该点称为平衡高度,也称为对流上限,越过该点之后气块获得向下的加速度,使气块减速
- 对于绝对不稳定型,如果低层是干绝热气层,即环境温度随高度以干绝热率递减,在某一高度发生凝结后围成面积就都为正,这个高度就叫对流凝结高度,此时对流凝结高度就是抬升凝结高度也是自由对流高度
- 在相同的温度层结下,湿度越高,抬升凝结高度就会低,气块越快沿湿绝热线上升,温度降低更慢,自由对流高度更低,正面积就越大
二十三、对流
只要存在一定的冲击力就可以产生对流,对流是否发展就要取决于大气稳定度,对流的发展需要不稳定能量,充沛的水汽,足够的对流冲击力
对流又分为动力对流和热力对流
23.1 动力对流
- 如果抬升凝结高度位于自由对流高度以下,要使气块上升到该高度需要依靠外力作用,一般认为自由对流高度是动力对流云的云底高度
23.2 热力对流(热雷雨、对流凝结高度——重点)
- 假设空气湿度不变,日出之后由于太阳对地面的加热,靠近地面的气层显著增温,由于湍流作用气层的温度递减率逐渐趋于干绝热递减率(湍流逆温中的理论)
- 直到从当时的抬升凝结高度直接引一条干绝热线到地面,地面对应的温度就是作为热力对流温度出现的判别指标
- 因为直接从抬升凝结高度引干绝热线,就意味着抬升高度以下气层被加热到递减率和干绝热递减率相同了,这样只要有一点扰动,气块就可以自由上升到抬升凝结高度,此时CIN为0,之后沿湿绝热线上升
- 也就是抬升凝结高度和自由对流高度重合,这个高度也称为对流凝结高度CCL
二十四、夹卷作用
- 实际观测中,云内的温度递减率一般大于湿绝热递减率而与云外温度递减率接近,同时云内水分也比计算值小1/3-1/2,这说明对流云发展过程中与云外空气有强烈的混合
- 湍流夹卷:通过云顶和侧边界,云内外通过热量、动量、水分和质量的湍流交换
- 动力夹卷:由于云内气流的加速上升,跟你举质量连续性要求,四周空气必然会流入云中进行补偿
二十五、气层稳定度
大范围的空气层上升或下沉运动,导致整层气层的升降,导致大气温度递减率和湿度垂直分布的变化,使气层的稳定度发生变化,导致强烈对流或使气层更加稳定
25.1 未饱和气层下沉逆温的形成(重要)
- 如果未饱和气块在下沉过程中是辐散的,那么根据质量守恒其水平方向面积增大,厚度减小
- 由于厚度变小,气块上界的下沉距离比气层下界的下沉距离长,因此上界的温度升高更多,如果距离足够大,上层的增温更多可能就会比下层的温度高,形成逆温
25.2 整层下沉/抬升后温度递减率改变(推导、不重要)
由质量守恒,下沉后质量不变
ρ 1 A 1 Δ z 1 = ρ 2 A 2 Δ z 2 \rho_1A_1\Delta z_1=\rho_2A_2\Delta z_2 ρ1A1Δz1=ρ2A2Δz2
Δ z 1 Δ z 2 = ρ 2 A 2 ρ 1 A 1 = A 2 p 2 T 1 A 1 p 1 T 2 \frac{\Delta z_1}{\Delta z_2}=\frac{\rho_2 A_2}{\rho_1 A_1}=\frac{A_2p_2T_1}{A_1p_1T_2} Δz2Δz1=ρ1A1ρ2A2=A1p1T2A2p2T1
这个式子要跟温度递减率联系在一起,之前公式中,位温随高度的变化会出现递减率和干绝热递减率的关系,因此往位温守恒上想
又由于在干绝热过程中虚位温守恒,因此经过下沉之后虚位温之差不变,有
∂ θ ∂ z 1 Δ z 1 = ∂ θ ∂ z 2 Δ z 2 \frac{\partial \theta}{\partial z_1}\Delta z_1=\frac{\partial \theta}{\partial z_2}\Delta z_2 ∂z1∂θΔz1=∂z2∂θΔz2
∂ θ ∂ z 2 = ∂ θ ∂ z 1 A 2 p 2 T 1 A 1 p 1 T 2 \frac{\partial \theta}{\partial z_2}=\frac{\partial \theta}{\partial z_1}\frac{A_2p_2T_1}{A_1p_1T_2} ∂z2∂θ=∂z1∂θA1p1T2A2p2T1
将位温随高度的变化式带进去
∂ θ ∂ z 1 = θ 1 T 1 ( γ d − Γ 1 ) \frac{\partial \theta}{\partial z_1}=\frac{\theta_1}{T_1}(\gamma_d - \Gamma_1) ∂z1∂θ=T1θ1(γd−Γ1)
得到
Γ 2 = γ d − ( γ d − Γ 1 ) p 2 A 2 p 1 A 1 = Γ 1 + ( γ d − Γ 1 ) ( 1 − p 2 A 2 p 1 A 1 ) \Gamma _2 = \gamma _d -(\gamma _d - \Gamma _1)\frac{p_2A_2}{p_1 A_1}=\Gamma_1 + (\gamma_d-\Gamma_1)(1-\frac{p_2A_2}{p_1 A_1}) Γ2=γd−(γd−Γ1)p1A1p2A2=Γ1+(γd−Γ1)(1−p1A1p2A2)
- 因此下沉/上升之后的温度递减率可以根据之前的温度递减率和气压之差算出
- 求 Γ 1 \Gamma_1 Γ1的时候用到 Δ T Δ z \frac{\Delta T}{\Delta z} ΔzΔT,用静力学方程将其换为与气压,温度之间的关系来求
二十六、位势稳定度(对流性不稳定——重中之重)
未饱和气层整层抬升的过程中,由于垂直方向空气湿度的差异会导致不同高度气块达到饱和先后的差异,对稳定度会有影响
下面假设在处置气层一定高度内为等温大气,但由于垂直方向湿度的差异,导致露点温度垂直方向有差异
26.1 位势不稳定(下湿上干)
- 下湿上干的话低层的露点温度高于上层
- 整层抬升的过程中,下层更快达到抬升凝结高度,之后沿湿绝热线上升
- 而上层由于露点温度更低,沿干绝热上升时间更长,温度降低更多之后才达到抬升凝结高度
- 这样整层抬升到之后,本来上下等温的气层会变成上方温度低,下方温度高
- 原本 γ > γ m \gamma > \gamma_m γ>γm的经过抬升之后变成 γ > γ m \gamma>\gamma_m γ>γm,由稳定变为了不稳定
- 也就是低层A点的假相当位温大于高层B点的假相当位温,就会发生位势不稳定
26.2 位势稳定(下干上湿)
- 下干上湿,下层的露点温度低于上层,上层先到达抬升凝结高度
- 整层抬升到,上层的温度就会比下层的高,形成逆温
- 这样就变得更加稳定
也就是低层A点的假相当位温小于高层B点的假相当位温,就会发生位势不稳定
26.3 小结
- 假相当位温的高低就可以判断一开始处于相同温度的气层谁先达到抬升凝结高度
- 如果假相当位温随高度降低的,那么就是位势不稳定的;反之就是位势稳定的
d θ s e d z < 0 不稳定 \frac{d\theta_{se}}{dz}<0 不稳定 dzdθse<0不稳定 - 这里用假湿球位温进行分析也是一样的效果
- 对流性不稳定是一种潜在不稳定,往往需要大范围的抬升运动,所以一般需要有天气系统或大地形作用才能产生
- 对流性不稳定造成的对流性天气往往比较强烈,范围也较大
二十七、大气逆温的产生原因(重要)
- 辐射逆温:白天地表吸收太阳辐射迅速增温,低层大气温度升高;夜晚地表向外发出长波辐射,导致地面迅速冷却,近地层形成逆温层;在晴朗无风的夜晚条件下最有利于辐射逆温的形成,因为晴朗夜晚地面的有效辐射大,无风让上层的热量难以通过湍流向下输送,有利于地面降温而形成逆温
- 平流逆温:冷地表上空有暖空气流过,低层空气迅速降温,导致上层空气温度高于低层温度导致逆温
- 地形逆温:山坡辐射降温快于山谷,冷空气沿地形下沉至山谷,山谷的暖空气被迫抬升,导致逆温
- 融雪逆温:类似平流逆温,暖空气流经雪地区,冰雪融化吸热,暖空气低层温度下降形成逆温
- 锋面逆温:不论是冷锋还是暖锋,暖空气总是在冷空气上方,从而形成逆温,因此在冷空气区可以观察到逆温
- 下沉逆温:在高压控制区,由于高空存在大规模的下沉气流;气流下沉的过程中,由于环境气压越来越大,气块在垂直方向的厚度会减少,水平方向增加;由于厚度的改变,导致一个气块中高处的气流下沉后,下沉的距离会比低处的气流下沉距离长,因此上层的温度增加更多,于是导致了下沉逆温
- 湍流逆温:上面单独讲了
二十八、气层法不稳定判据
- 可画图解决,气块走气块的,气层走气层的,之后看谁的温度高来判断
- 较为复杂,考的可能性不大
这篇关于国防科大、中大0706大气科学及南信大大物院初试复习宝典——第五章:大气热力学篇的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









