马普所Nerf新作《TensoRF》阅读笔记

链接：

1. Arxiv链接：https://arxiv.org/pdf/2203.09517.pdf
2. 主页链接：https://apchenstu.github.io/TensoRF/
3. 代码链接：https://github.com/apchenstu/TensoRF

视频：

作者是上科大虞老师学生陈安沛，现在德国马普所AG组做博士后，非常优秀的一篇nerf文章。

创新点：

本文提出了一种nerf重建与表达的新范式，核心思想是将单个4D神经辐射场利用张量分解技术，使用多个紧凑的因子化的低秩张量组件来重建，即下图：

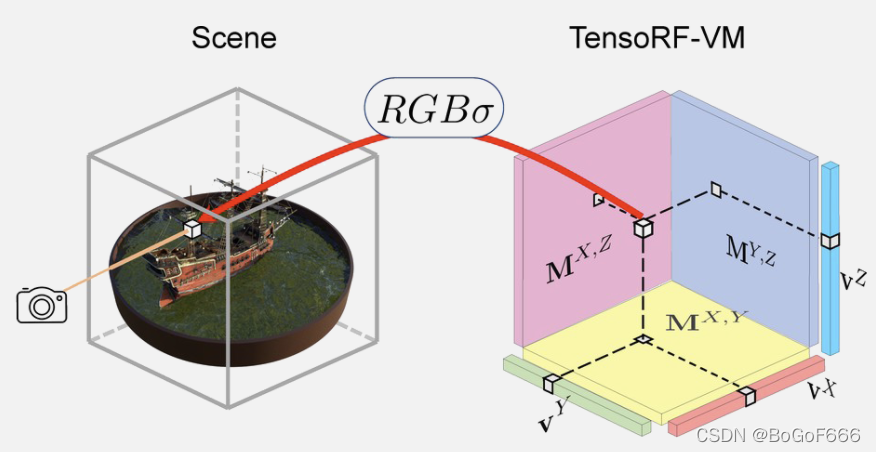
左边是场景，右边是用了一些低秩张量组件来描述左边场景的外观(RGB)与几何变化($\sigma$)，XYZ每个维度都存在一组matrix和vector，体积密度（$\sigma$）和颜色(RGB)可以通过计算matrix与vector的外积（outer product）得到，这么做的好处是极大的提升了重建效率(训练时间)与效果(PSNR)，降低了存储成本(模型存储大小)，如下图：

方法：

- 分解方式：

首先，本文提出了两种分解方式（如下图）：

1. CP分解：将场景张量T分解为多个向量外积的和，$\tau ={\sum }_{r=1}^R{V}_r^1\circ V_r^2\circ V_r^3$, $\tau \in {\mathbb{R}}^{I\times J\times K}$
2. VM分解：将场景张量T分解为多个向量-矩阵外积的和, $\tau ={\sum }_{r=1}^{R_1}{V}_r^1\circ M_r^{2,3}+{\sum }_{r=1}^{R_2}{V}_r^2\circ M_r^{1,3}+{\sum }_{r=1}^{R_3}{V}_r^3\circ M_r^{1,2}$, 其中$M_r^{2,3}\in {\mathbb{R}}^{J\times K}$, $M_r^{1,3}\in {\mathbb{R}}^{I\times K}$, $M_r^{1,2}\in {\mathbb{R}}^{I\times J}$
   

- 训练框架：

1. 首先输入是
   

实验指标：

总结

这篇工作还有个好处，就是不像同期工作Plenoxels和Instant-ngp需要定制化的cuda kernel，代码完全基于标准的pytorch编写，省去了很多编译以及部署时的潜在麻烦。