判断平面多边形的凹凸性

本文主要是介绍判断平面多边形的凹凸性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对于平面多边形的三角化处理也是计算机图形学里面的一个领域，最近由于项目的需要，需要对平面多边形进行剖分，特此对其作了些研究。

在对平面多边形进行处理的时候，很多时候需要知道多边形的凹凸性，本文介绍两种方法来进行平面多边形凹凸性的判定，文章后面会给出示例代码。

1、使用角度和判断凹凸性

我们知道，任意n个顶点的凸多边形可以分解成(n-2)个三角形，一个三角形的内角和是180°，所有三角形的内角和是(n-2)*180°，这一点，对于凸多边形或者凹多边形来说都是一样的，但是对于一个凸多边形来说，不存在内角大于外角，而凹多边形则会存在。

因此，将多边形每个顶点处较小的角（内角或外角）相加，凸多边形得到(n-2)*180°,而凹多边形则小于它。至于如何判断小角，我们可以使用几何工具---向量点乘。我们知道，向量点乘可以用来等价求两个向量的夹角，它的值（即角度）总是以较短的弧度来度量的。

以下是代码的示例：

bool IsHollow(std::vector<Position3> curveloopPoints)const{//使用角度和判断凹凸性：凸多边形的内角和为（n-2）*180°auto num = curveloopPoints.size();float angleSum = 0.0;for (int i = 0; i < num; i++){Vector3 e1;if (i==0){e1 = curveloopPoints[num - 1] - curveloopPoints[i];}else{e1 = curveloopPoints[i - 1] - curveloopPoints[i];}Vector3 e2;if (i==num-1){e2 = curveloopPoints[0] - curveloopPoints[i];}else{e2 = curveloopPoints[i + 1] - curveloopPoints[i];}//标准化并计算点乘e1.normalize(); e2.normalize();float mdot = e1%e2;//计算较小值float theta = acos(mdot);//加和angleSum += theta;}//计算内角和float convexAngleSum = float((num - 2))*YZ_PI;//判断凹凸性if (angleSum<(convexAngleSum-(float(num)*0.00001))){/*if (HollowPoints.size()>0){*///m_IsHollow = true;//}return true;//是凹}return false;//否则是凸}

2、使用矢量判断凹凸性，检测多边形的凸点

检测多边形上是否有凹点，如果没有则为凸多边形。其原理是，凸多边形的每个顶点的转向都应该一致，不一致的点 就是凹点。

我们判断一个顶点的转向，使用的是另一个几何工具---向量叉乘。

这里我们需要平面的法向量，根据法向量来检测多边形的每个顶点：

用相邻的两个边向量计算该顶点的法向量，接着用多边形的法向量和点的法向量点乘，若点乘值为负（方向相反），则该顶点就是一个凹点。

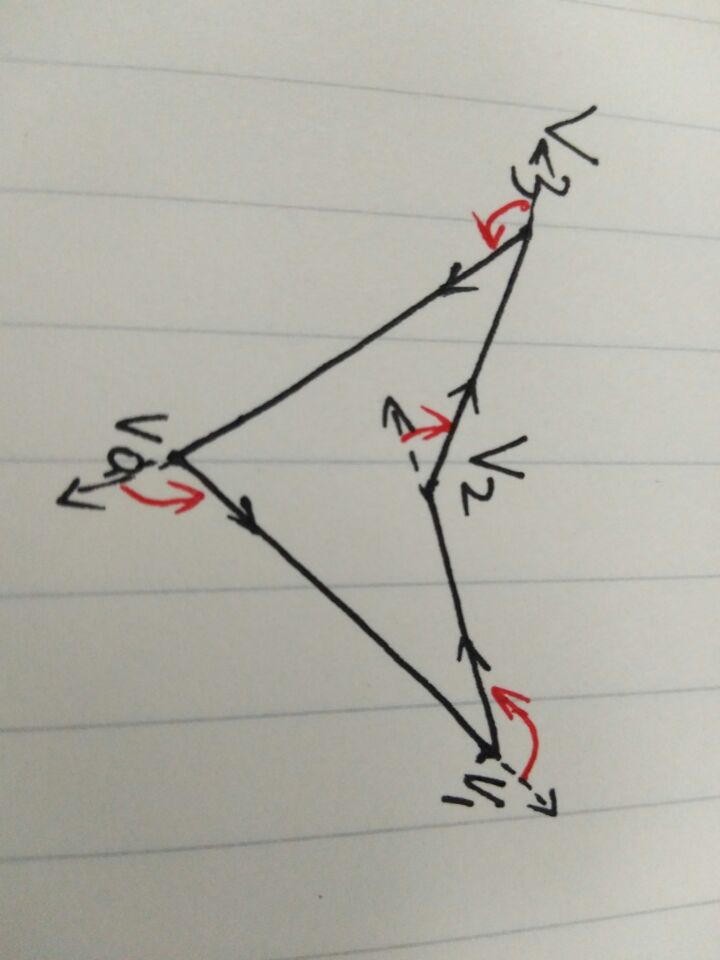
如下图所示，红色旋转方向为逆时针的顶点是多边形的凸点。

以下是方法的示例代码，函数返回的是凹点坐标：

const std::vector<Position3>& IsHollow_Vec(std::vector<Position3> curveloopPoints)const{//假设传进来的顶点数组都是按照顺时针或者逆时针遍历的，且没有重复点//使用法向量判断凹凸性，检测多边形上是否有凸点，每个顶点的转向都应该一致，若不一致则为凹点std::vector<Position3> HollowPoints;auto num = curveloopPoints.size();Vector3 HollowNor = (curveloopPoints[num-1] - curveloopPoints[0])* (curveloopPoints[1] - curveloopPoints[0]);Vector3 Nor;for (int i = 0; i < num;i++){if (i==0)//第一个点{Nor = (curveloopPoints[0] - curveloopPoints[num - 1])* (curveloopPoints[1] - curveloopPoints[0]);if ((Nor%HollowNor)>0.0)//如果点乘大于0{HollowPoints.push_back(curveloopPoints[i]);}}else if (i==num-1)//最后一个点{Nor = (curveloopPoints[i] - curveloopPoints[i - 1])* (curveloopPoints[0] - curveloopPoints[i]);if (((Nor%HollowNor) > 0.0))//如果点乘大于0{HollowPoints.push_back(curveloopPoints[i]);}}else//中间点{Nor = (curveloopPoints[i] - curveloopPoints[i - 1])* (curveloopPoints[i+1] - curveloopPoints[i]);if (((Nor%HollowNor) > 0.0))//如果点乘大于0{HollowPoints.push_back(curveloopPoints[i]);}}}return HollowPoints;}

 

以上两种判断多边形凹凸性的方法来自于《3D数学基础图形与游戏开发》一书，并由自己编程实现。

这篇关于判断平面多边形的凹凸性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---