谭平老师课——相机模型

本文主要是介绍谭平老师课——相机模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

RANSAC：选出最大的inlier的集合。做模型拟合离不开这个算法。(RANSAC为Random Sample Consensus的缩写，它是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。它于1981年由Fischler和Bolles最先提出)

思想：随机挑最少的点去拟合，然后评价这次拟合的怎么样
选出投票数最多的模型，选出符合这个模型的点为inliers，但是模型不是最后的模型
假定：inliers互相之间是一致的；outliers得到的模型互相不一致(不团结)
理论上不能处理outlliers数超过50%的，且外点比较团结的情况
概率：希望某次挑出来的最小拟合点正好都是inliers，有个公式能得到需要迭代多少次

拟合模型用的样本点越少(8点法，4点法等)，算法越稳定，因为可以容忍更大比例的outliers

注意：迭代过程中可以动态的估计外点的比例(先假设为50%)，因为每次随机采样后评估这个模型的时候，
就可以得到外点和内点，这时真正的的内点比例肯定大于等于这次的。(比例用于设定迭代的次数)

第10章几何和相机模型
齐次坐标：定义线、点、点和线的关系
有齐次坐标后点和线的关系就很好表示了，点在线上，就是点的齐次坐标(3维)点乘线的坐标=0。
两直线叉乘得到交点坐标
两个点的叉乘得到一条直线
点和线是对偶的，在平面射影几何中对点成立的定理对线也成立，因为他俩都是用3维向量表示
齐次坐标的最后一个坐标是0的话表示无穷远点
有无穷多个无穷远点，而且这些点都在（0,0,1）这条直线上，数量积为0

椭圆：conics
二次曲线和一个3乘3的对称矩阵对应，有6个元素，但是只有5个自由度，因为是up to scale的，也就是关心的是各元素之间的比值而不是具体的值

两条直线平行=其交点在无穷远点，所以变换要保持平行还是平行，只要保持那个无穷远直线不变就行

3维点加上第4维的坐标，变成齐次坐标，也就是变成射影空间的一个点
3维空间中点和平面对偶

射影几何：(射影几何是研究图形的射影性质，即它们经过射影变换后，依然保持不变的图形性质的几何学分支学科)
s相似变换(放缩旋转平移)——保留角度 a仿射变换——保留平行底下行都是001
p射影变换——只保留3个点共线的结构（就是Homography ） (一般拍的照片中只保留了projective的信息)，然后依次恢复a和s
直线叉乘得到交点坐标底下行不是001
射影几何中的所有元素都是equel up to scale的

相机(数学)模型：
不是线性的，因为有除以z操作
写成齐次坐标形式后，就成了矩阵乘法(相机的投影矩阵)，变成线性的了

将世界坐标系的原点移到相机坐标系的原点，重合 (目的是将世界坐标系中的点变换到相机坐标系)

60度的FOV镜头，一般不会有畸变，但是鱼眼那种广角的会有畸变

相机矩阵由外参和内参构成

有一个分析代数误差(没有几何意义，就是用数学变换)、几何误差(两个对应点中假设其中一个是精确已知的，另一个是包含噪声的，需要互相投影)、
重投影误差(两个对应点都有精确的和投影后的有噪声的点)的讲解 ——单应矩阵时讲的

相机矩阵(内参+外参)的每行和每列都有几何意义
计算相机光心的坐标在相机模型2中第37分钟
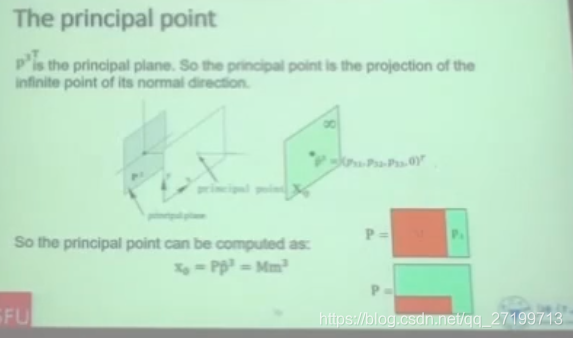
principal plane平面和相机成像平面平行，但是在相机的中心点上。点的深度是到这个平面的距离
Principal point指的是图像的中心点坐标，后又变成光心的坐标了
指的是凸透镜的中心，也就是小孔，也就是光心

标定：见课件

光流：运动有多大 warping（金字塔）
近处的物体运动大，远处的物体运动小

应对外点的方法：RANSAC和鲁棒核函数

两条直线平行=其交点在无穷远点，所以变换要保持平行还是平行，只要保持那个无穷远直线不变就行

3维点加上第4维的坐标，变成齐次坐标，也就是变成射影空间的一个点
3维空间中点和平面对偶在这里插入图片描述
最后一行就是真实的点到图像平面的映射，映射到距离光心d的位置，3维坐标变成两维的图像坐标
之前学的affine等之类的都是线性变换，而相机模型不是线性的，因为有除法，但是变成齐次坐标就成了线性的了。
大家都喜欢线性的。
负号是因为为了变成右手坐标系，将z轴朝向成像平面的反向了。
在这里插入图片描述
上面那个矩阵就是相机的投影矩阵
这样就成了线性的了
将摄影几何方法用进来就成了线性的了

这个投影矩阵是up to scale的，如上矩阵同乘-d，最后得到的2维非齐次投影点坐标一样

正交(平行)投影，直接将z坐标去掉就可以，d相当于是无穷大

以上都是3维点在本个相机坐标系中定义描述的
接下来引入世界坐标系
以上只是引入了一个参数d，接下来还要引入相机的位置和朝向信息
在这里插入图片描述

（0）得到相机矩阵：
当3维点在世界坐标系中定义时，首先需要将其变换到本相机坐标系中(也可以理解为将相机坐标系变到和世界坐标系重合，这样世界坐标系中的3D点就能向相机坐标系投影了)，这就需要知道相机的位姿，而且相机的位姿(相机的位置和朝向)是在世界坐标系中描述的；然后再投影到图像平面。
这两种变换当引入齐次坐标后都变成线性的了，也就是矩阵相乘。

在这里插入图片描述
先进行平移：-c，因为相机的中心在c(世界坐标系中定义)处，做-c的平移将其移到世界坐标系的中心。然后原点就重合了。

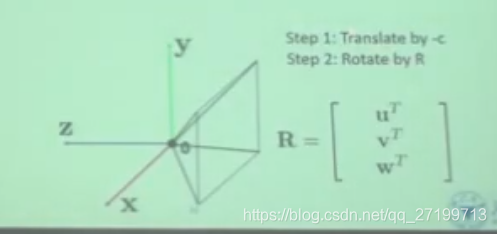
然后是旋转，将3个轴aline上。

这个矩阵是K矩阵：
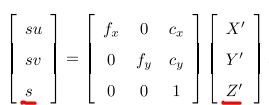
在这里插入图片描述

相机的投影矩阵：

内参：就是相机运动时是不会变的，比如焦距

下面讲如何从相机矩阵3乘4矩阵中恢复出参数，比如：中心c，朝向R等。上个过程的逆过程

（1）确定相机中心：三维
在这里插入图片描述
P把相机中心坐标(待求)变换到（0，0，0）位置。

（2）相机的每一个列向量啥意思：
x=[0 1 0 0]T 表示一个沿着y轴的一个无穷远点，沿着y轴一直走到无穷远就到了这个点
相机矩阵的第2列表示y方向的无穷原点在图像上的投影坐标
在这里插入图片描述
第4列是世界坐标系的原点在图像坐标系下的坐标

（3）朝向，每一行是什么意思：
第3行是一个平面叫 principal plane(和图像平面平行但是在相机的中心点上)，该平面上的会被投影到无穷远点，其中的三个元素是该平面的法向量，也就是平面的朝向，也即相机在世界坐标系下的朝向，这就是几何意义
在这里插入图片描述
（4）确定光心 principal point ，二维

（5）求深度——3维点到principla plane的距离
知道了相机矩阵，则任何3维点的深度都可以求出
思想：将3维点和相机中心的连线向相机朝向方向投影

总结：