永磁同步电机高频注入位置观测

2024-02-28 21:12
文章标签 观测 注入 位置 高频 永磁 同步电机

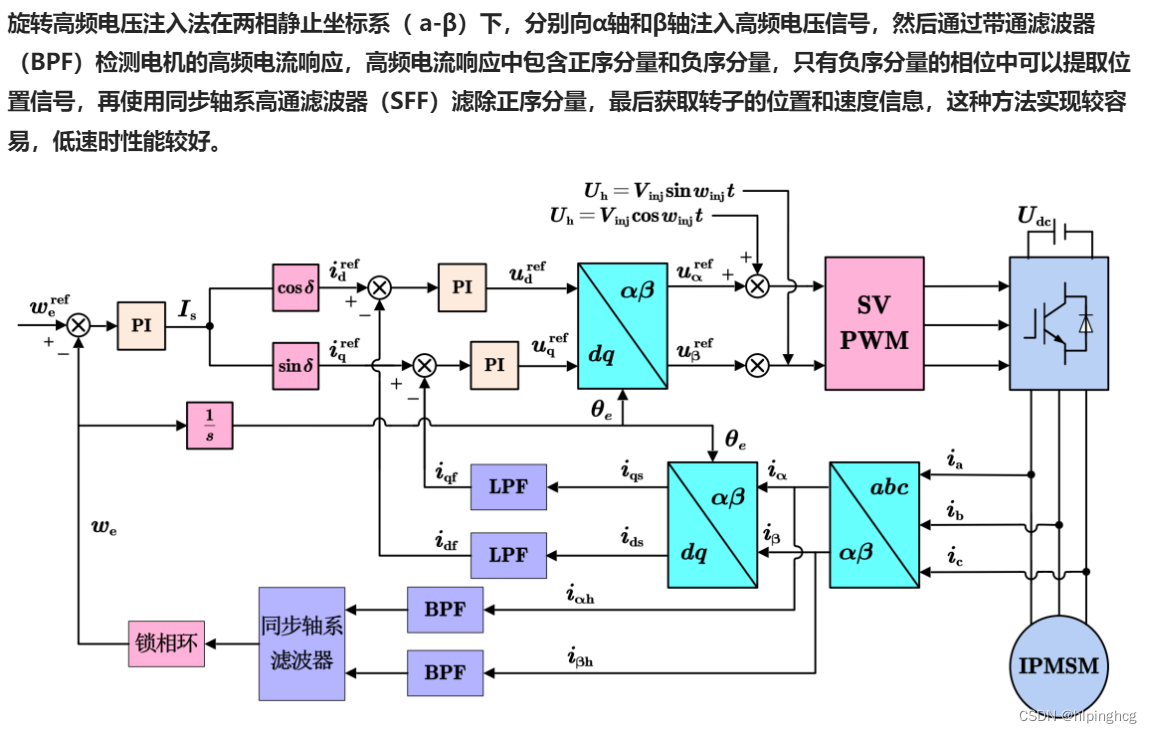
本文主要是介绍永磁同步电机高频注入位置观测，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 1、前言
  • 2、旋转高频注入法
    • 2.1 旋转高频注入法原理分析
    • 2.2 旋转高频注入法仿真
  • 3、脉振高频正弦注入法
    • 3.1 脉振高频正弦注入法原理分析
    • 3.2 脉振高频正弦注入法仿真
  • 4、脉振高频方波注入法
    • 4.1 脉振高频方波注入法原理分析
    • 4.2 脉振高频方波注入法仿真
  • 参考

写在前面：本人能力、时间、技术有限，没有对一些细节进行深入研究和分析，也难免有不足和错误之处，欢迎交流和指正。本人写博客主要是学习过程的记录。

1、前言

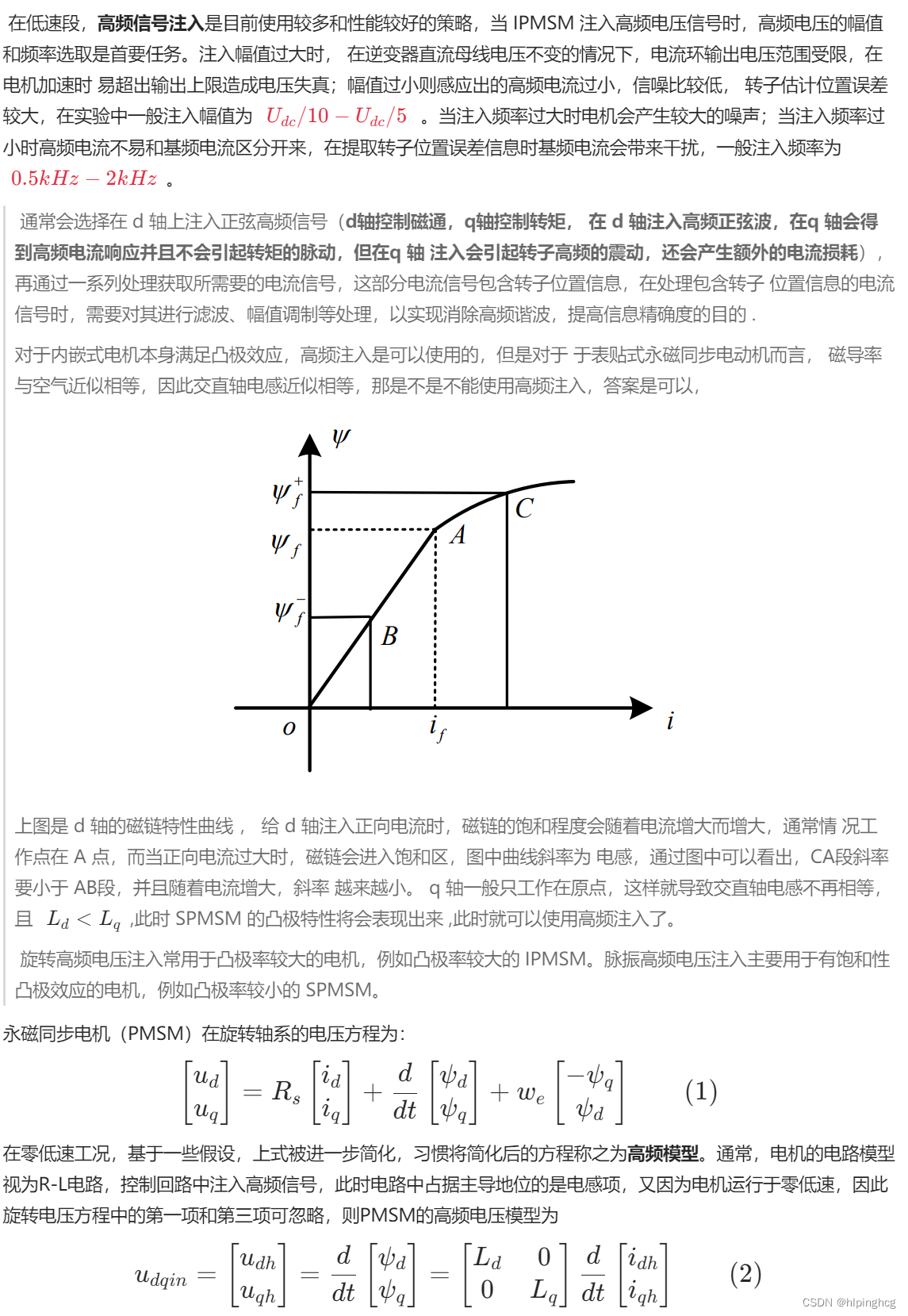
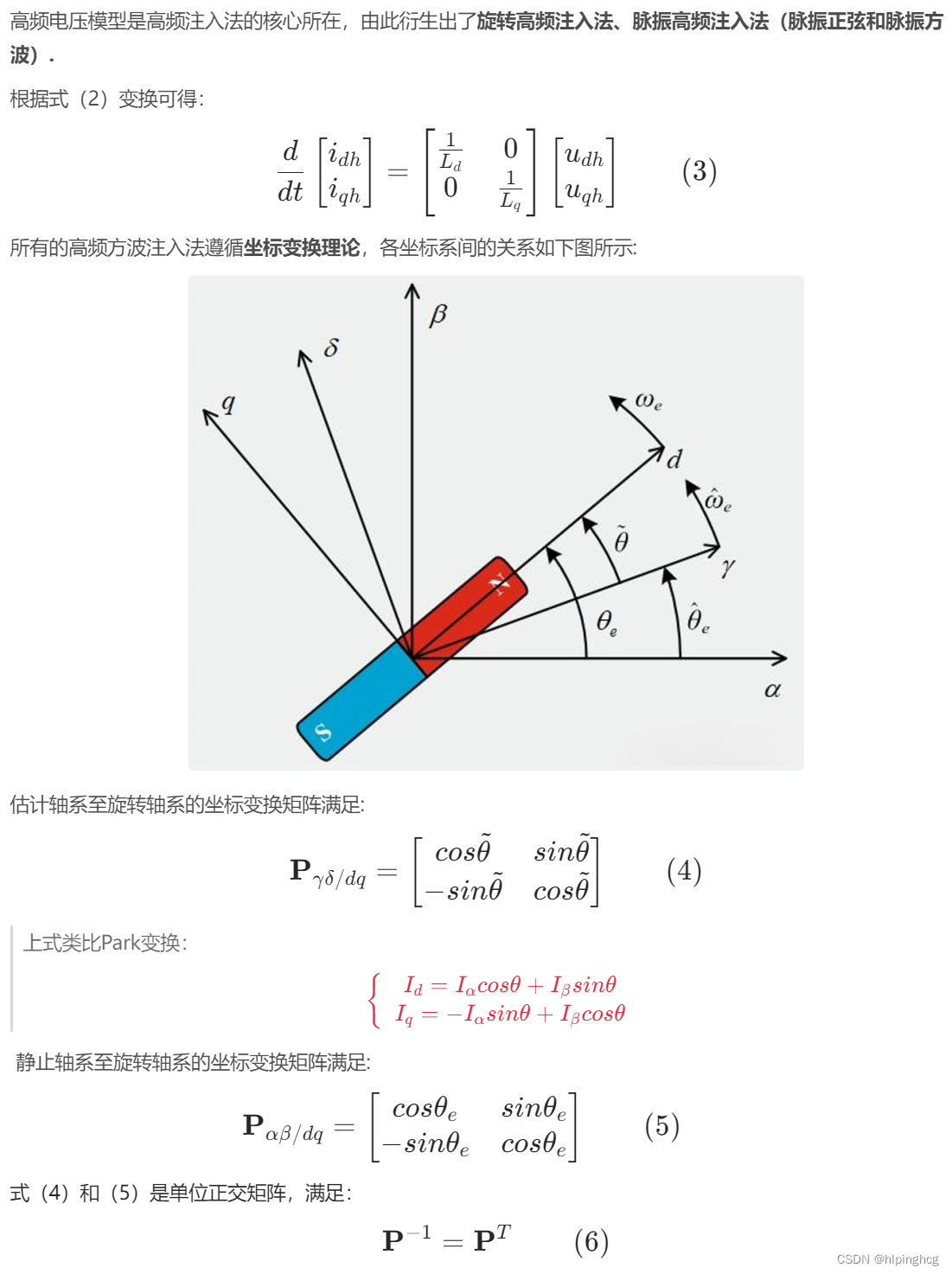
在这里插入图片描述
在这里插入图片描述
旋转高频注入法、脉振高频正弦注入法和脉振高频方波注入法的信号注入、响应信号提取轴满足下表：
在这里插入图片描述

2、旋转高频注入法

2.1 旋转高频注入法原理分析

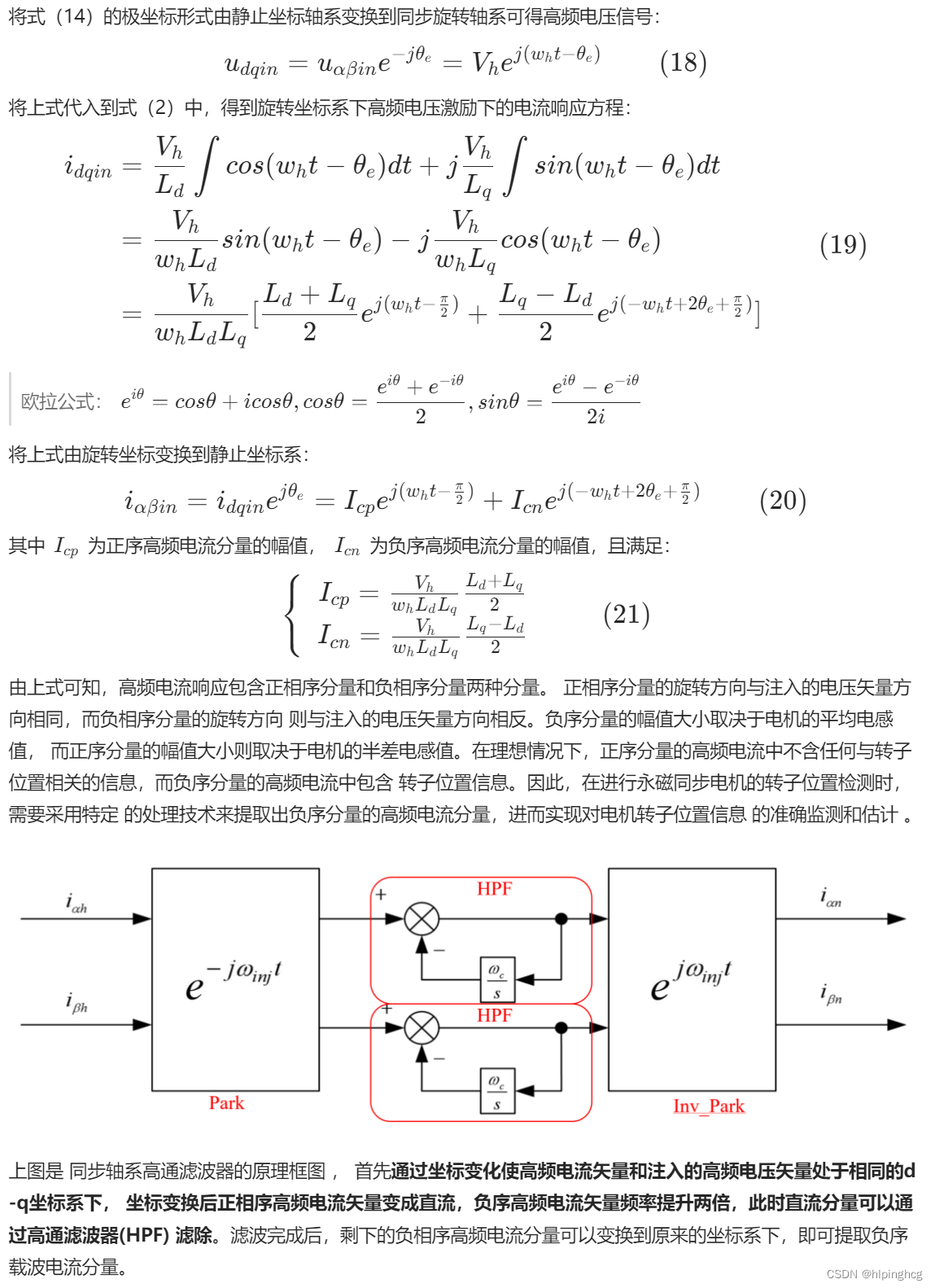
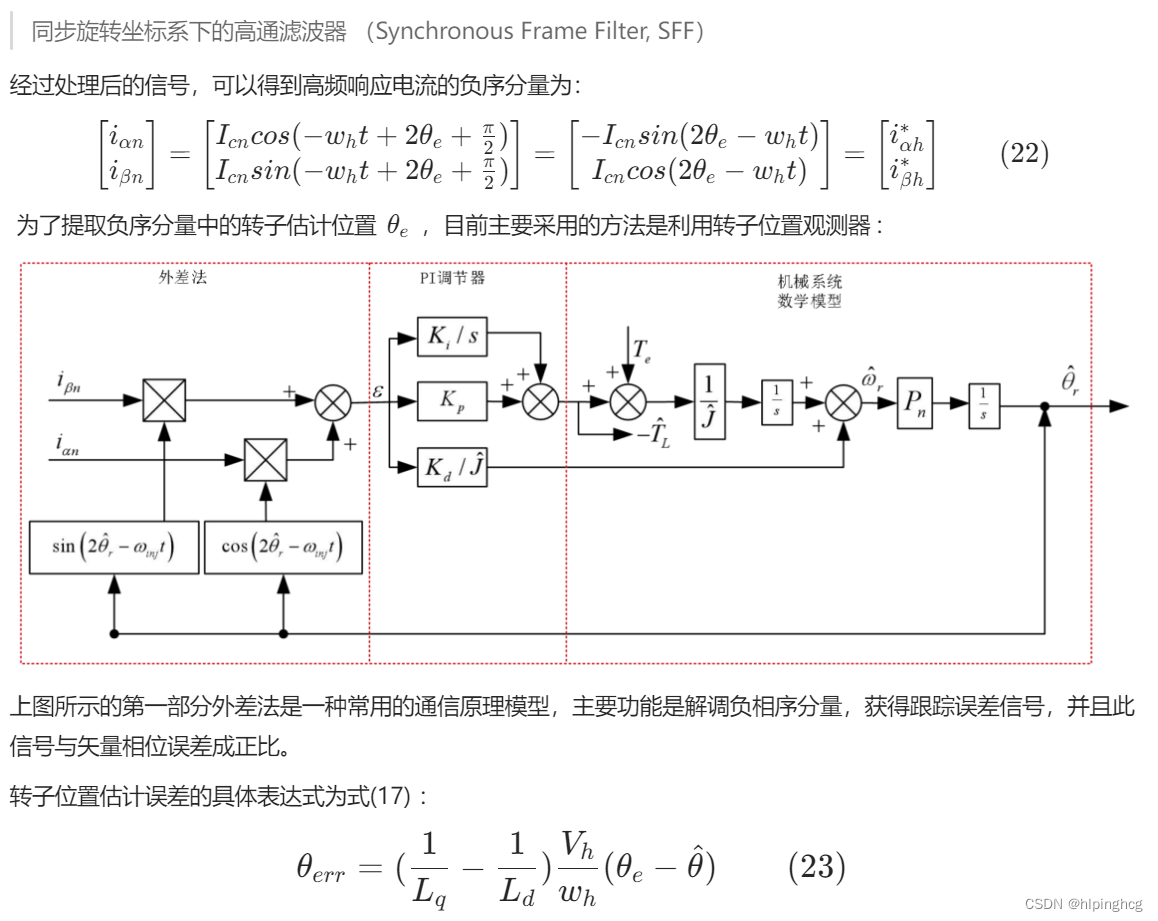
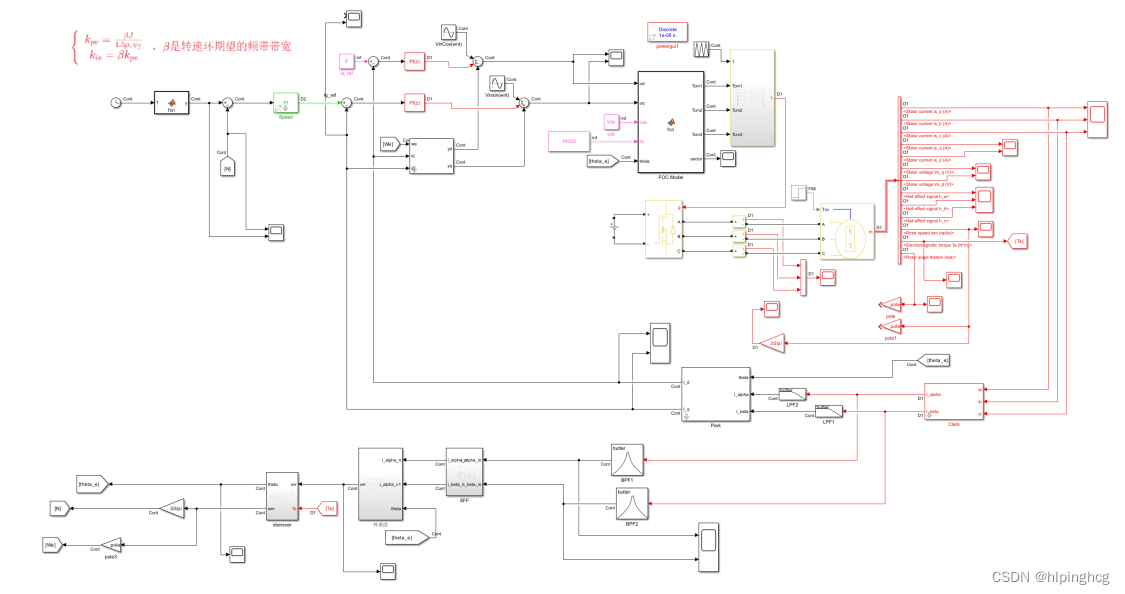
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.2 旋转高频注入法仿真

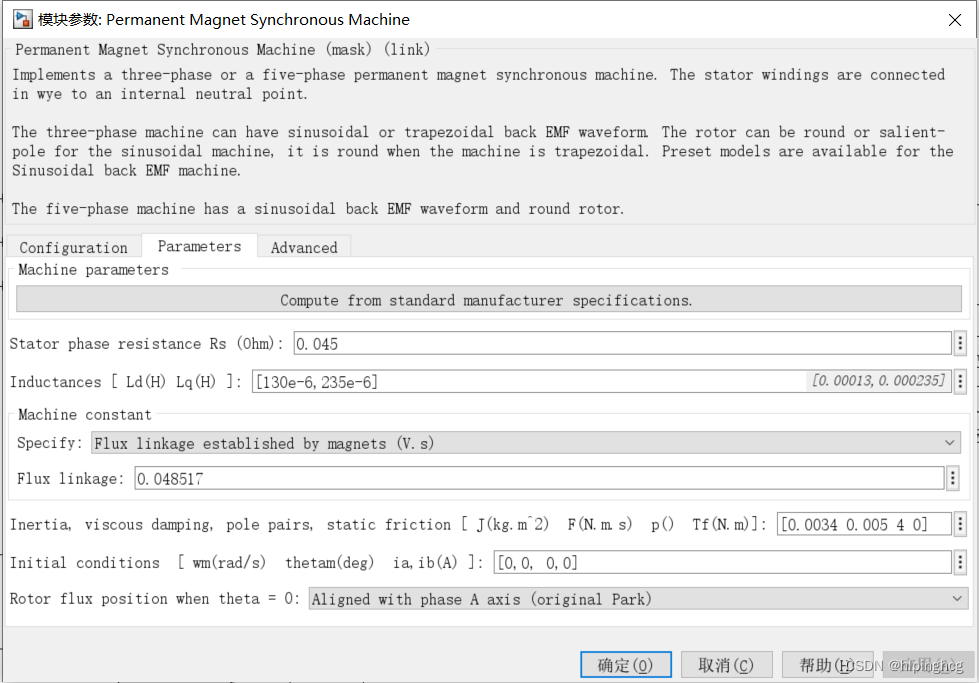
在这里插入图片描述
电机参数：

Vdc=311;
Rs=0.33;
Ld=5.2e-3;
Lq=17.4e-3;
flux=0.646;
J=0.008;
B=0.008;
pole=2;
fx=0;
wc=1000;

参数计算脚本：

function fcn(~)%----------------------------------------基本参数--------------------------------------------------------%
%4V/1000rpm
r=0.33;
Ld=5.2e-3;
Lq=17.4e-3;
Ts=0.0001;
%Ke=4/1000; 
pole=2;
J=0.008;
B=0.008;
flux=0.646;
fx=0;%----------------------------------------PI等参数计算--------------------------------------------------------%
%由反电动势常数计算磁链
%flux=10*sqrt(6)*Ke/(pi*pole);
% r : 欧姆
% LS：H%电流环PI计算
A=[Ld/r Lq/r];
wc=2*pi/(min(A));
kcpd=wc*Ld;
kcpq=wc*Lq;
kci=wc*r;%速度环PI计算
wn=wc/20;
Ba_temp=(wn*J-B)/(1.5*pole*flux);
%观察仿真结果，我们可以看出，系统响应速度较快，但是振荡得比较严重，系统不稳定。
%所以我们可以调节有功阻尼增益，减小有功阻尼增益，由表达式可以看出，转速环带宽与阻尼增益成正比。
% 根据自动控制原理可知，带宽越大，系统的快速性越好，稳定变差。B_a=0.13/10 B_a=0.013。PI参数不变。
Ba=Ba_temp/10;
kvp=wn*J/(1.5*pole*flux);
kvi=wn*kvp;%----------------------------------------数据打印--------------------------------------------------------%
str='wc value is: ';
str=[str,num2str(wc)];
disp(str);str='kcpd value is: ';
str=[str,num2str(kcpd)];
disp(str);str='kcpq value is: ';
str=[str,num2str(kcpq)];
disp(str);str='kci value is: ';
str=[str,num2str(kci)];
disp(str);str='wn value is: ';
str=[str,num2str(wn)];
disp(str);str='Ba value is: ';
str=[str,num2str(Ba)];
disp(str);str='kvp value is: ';
str=[str,num2str(kvp)];
disp(str);str='kvi value is: ';
str=[str,num2str(kvi)];
disp(str);

计算结果：
在这里插入图片描述
模型总览：
模型下载地址: 永磁同步电机旋转高频注入初始位置辨识simulink仿真
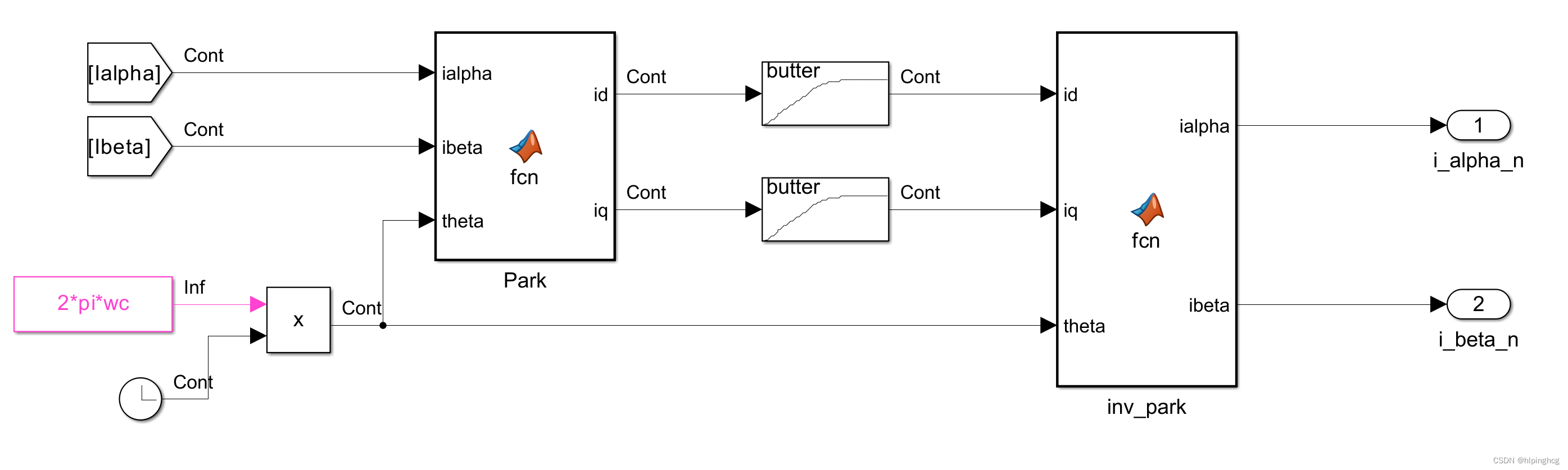
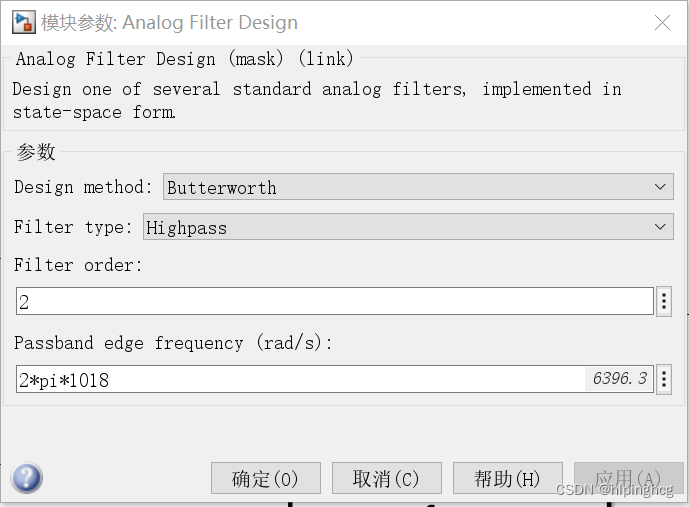
在这里插入图片描述
同步轴高频滤波：
在这里插入图片描述
这里的高频滤波截至频率为
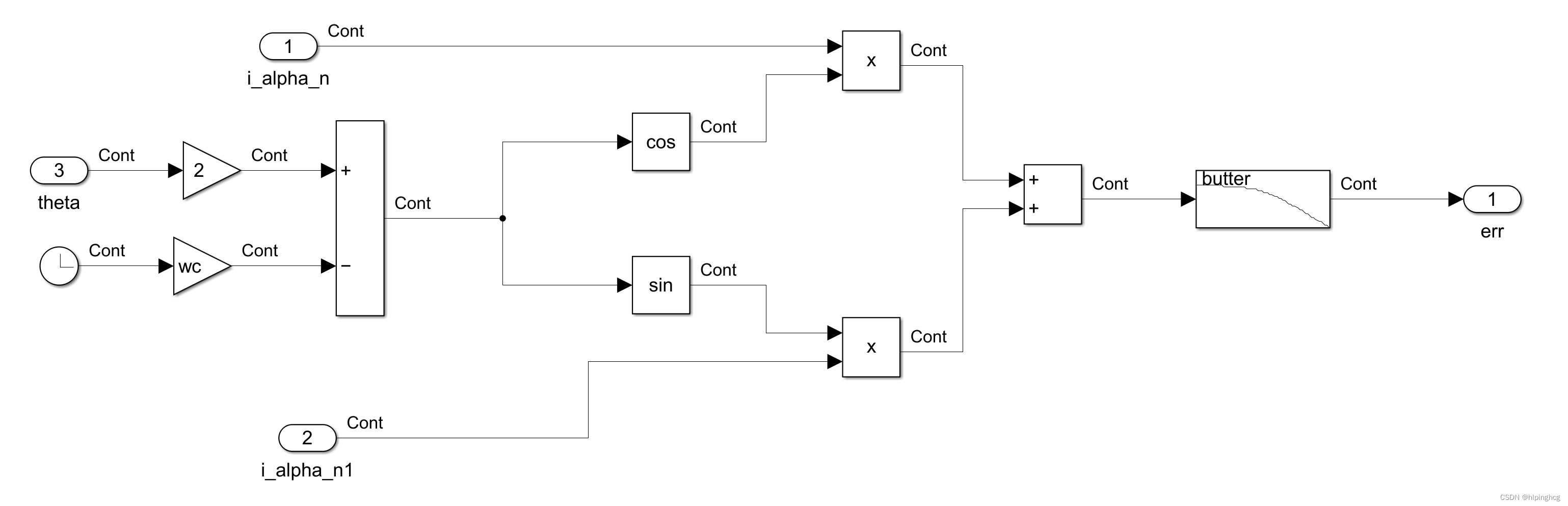
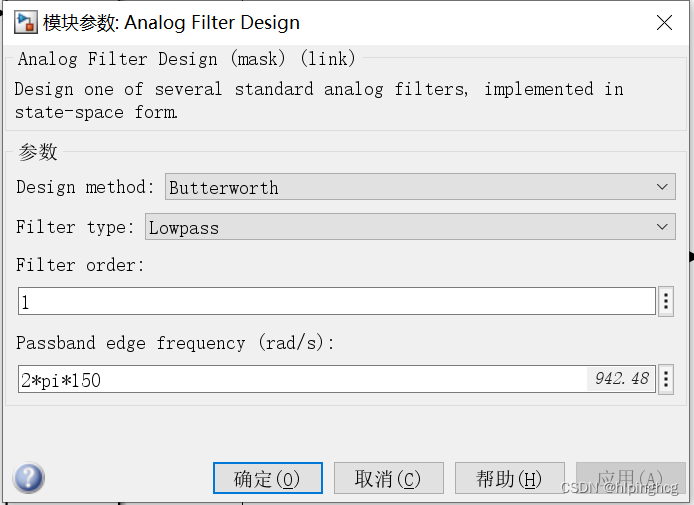
在这里插入图片描述
外差法模块：
在这里插入图片描述
低通滤波器截至频率为：
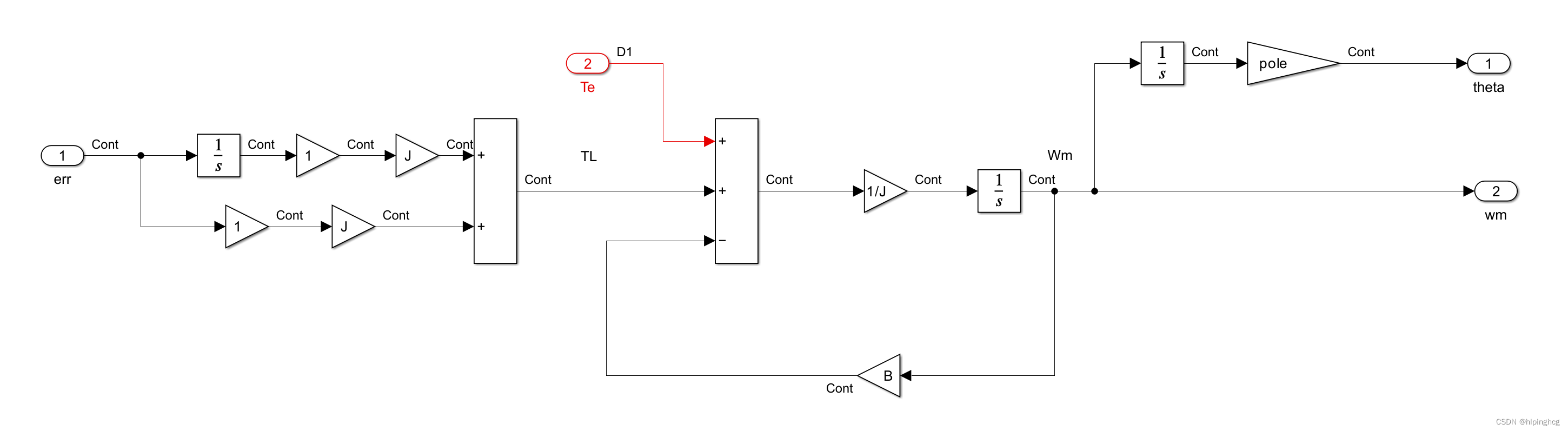
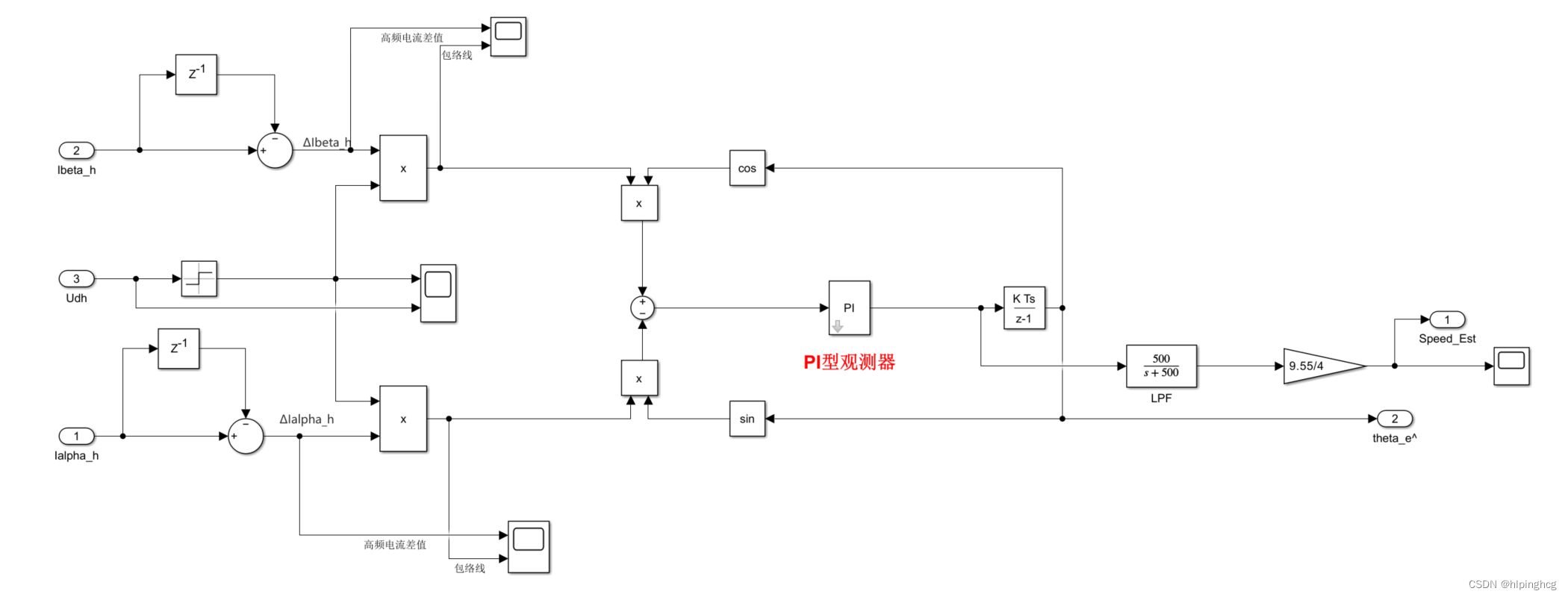
在这里插入图片描述
位置观测模块：
在这里插入图片描述
这里很多人会问，角度误差经过PI后为什么式负载转矩TL，我的理解就是在离散系统中，单位时间的角度误差为角速度，经过PI后变为角加速度，再乘以J（转动惯量）就变为负载转矩TL。
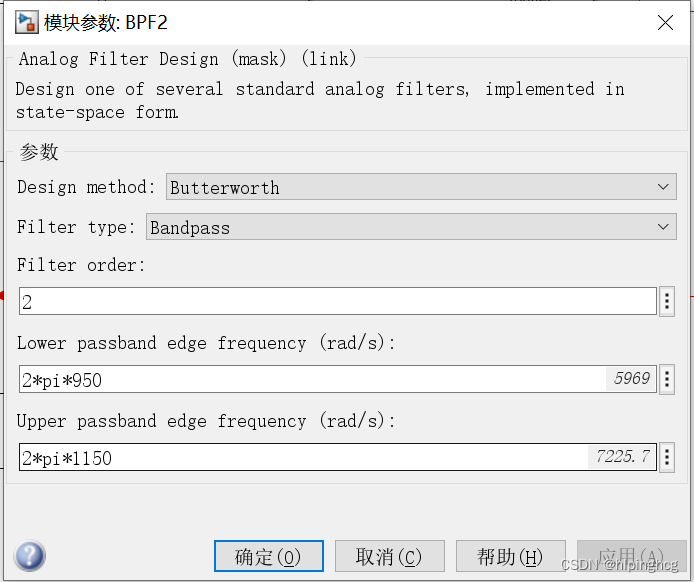
带通滤波器：
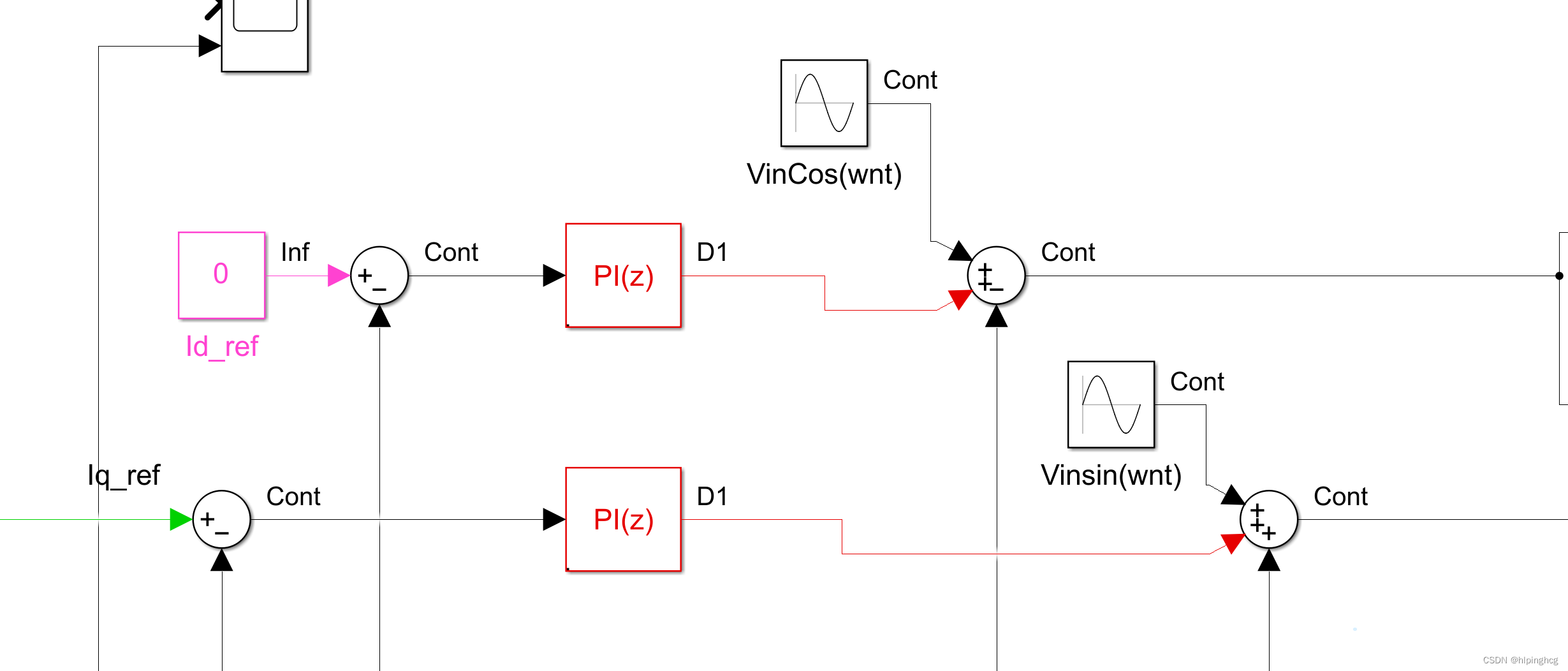
在这里插入图片描述
注入信号：
在这里插入图片描述
仿真结果：
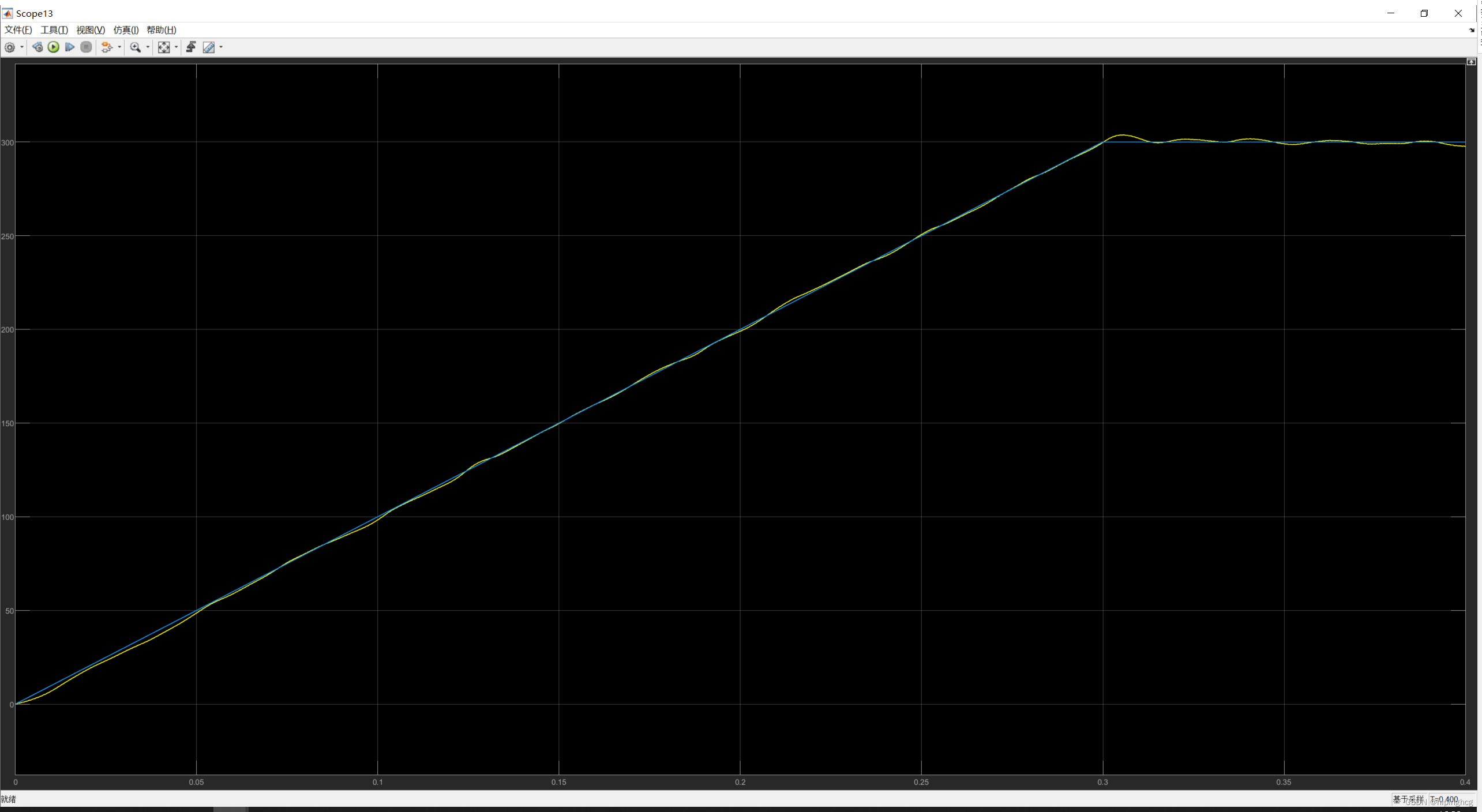
给定速度与实际速度
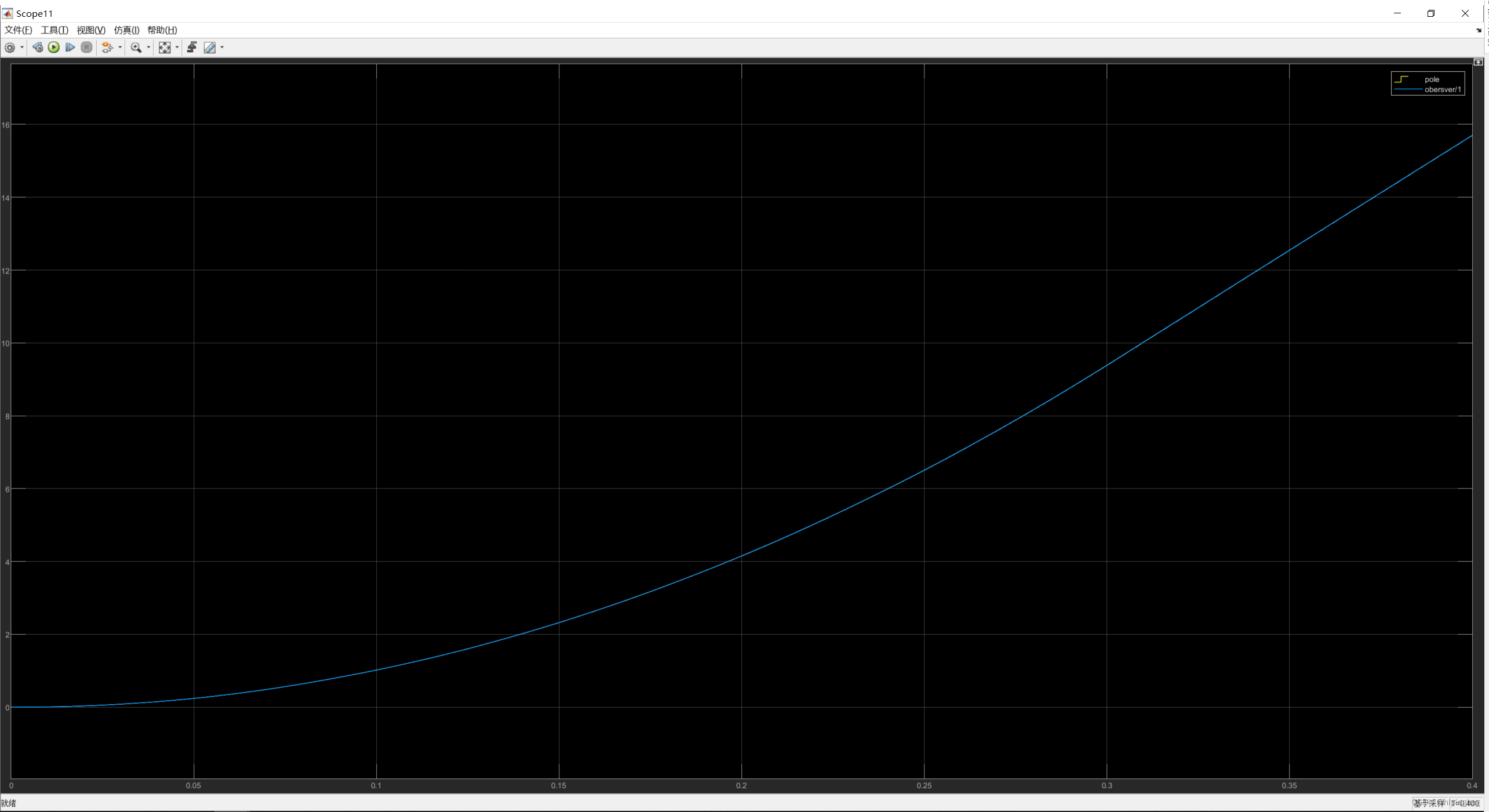
在这里插入图片描述
观测位置与实际位置
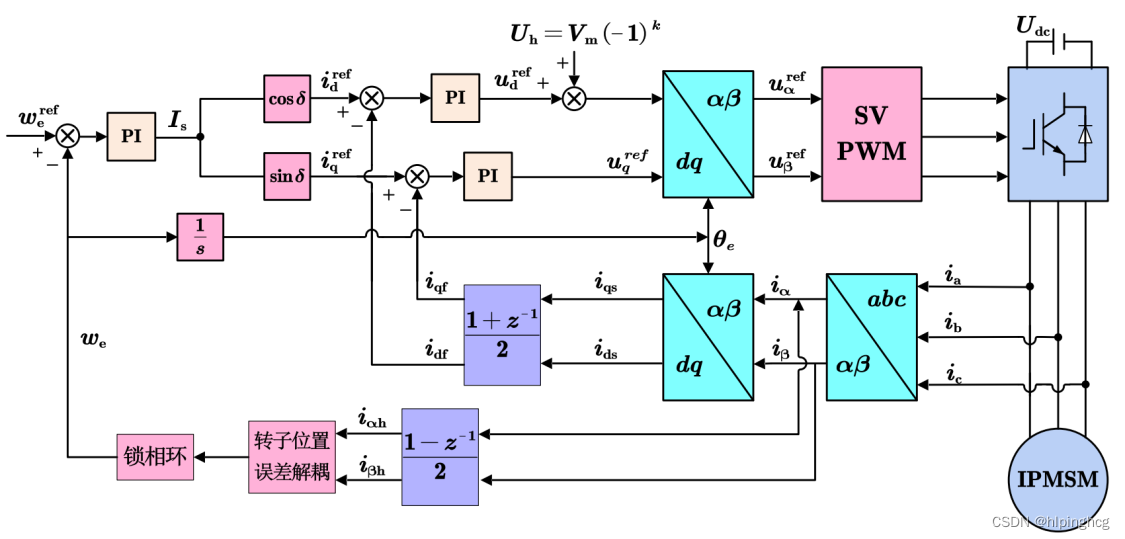
在这里插入图片描述

3、脉振高频正弦注入法

3.1 脉振高频正弦注入法原理分析

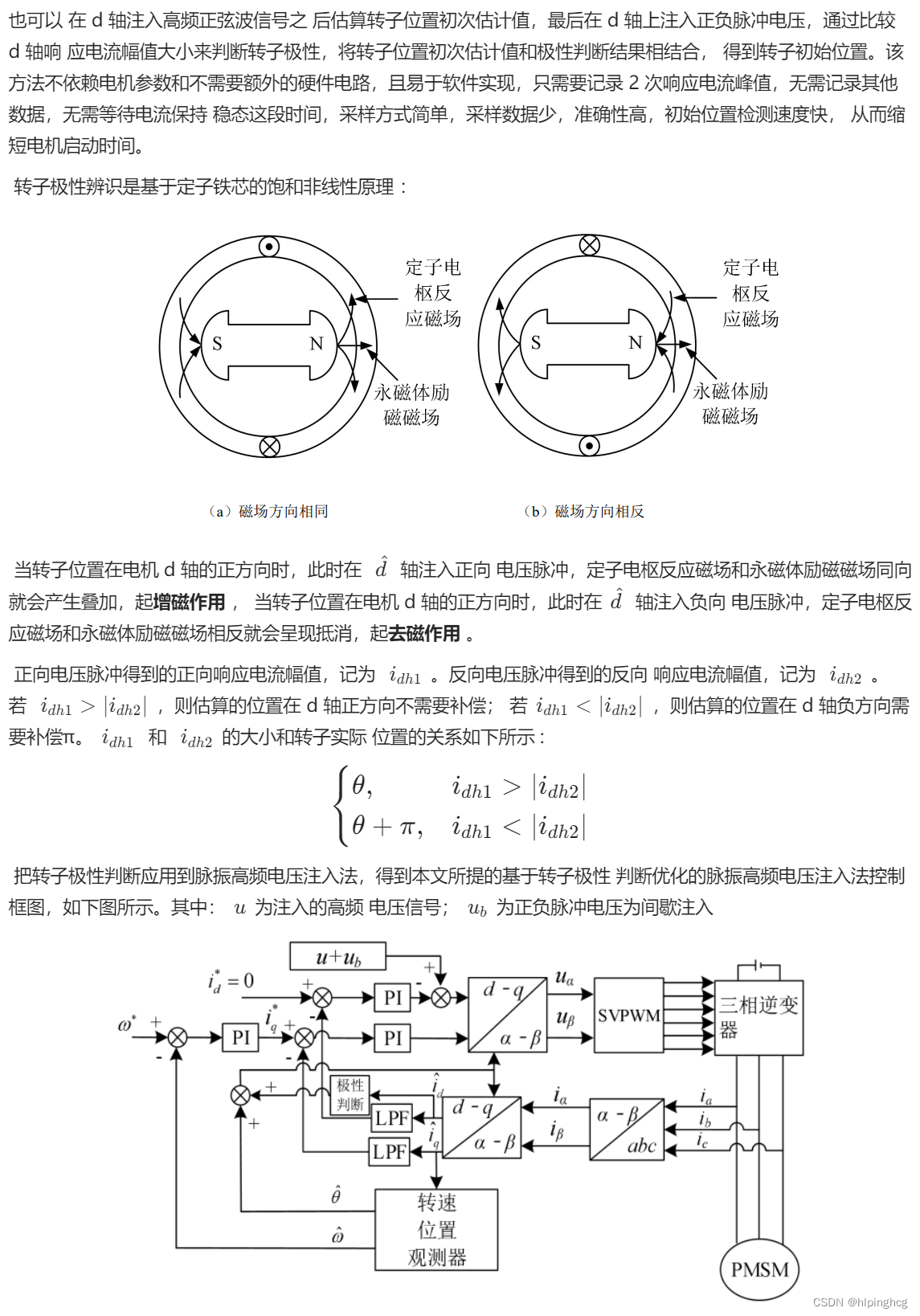
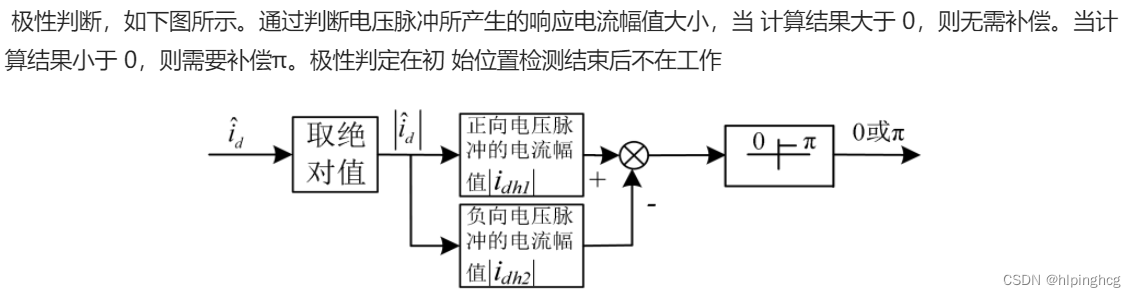
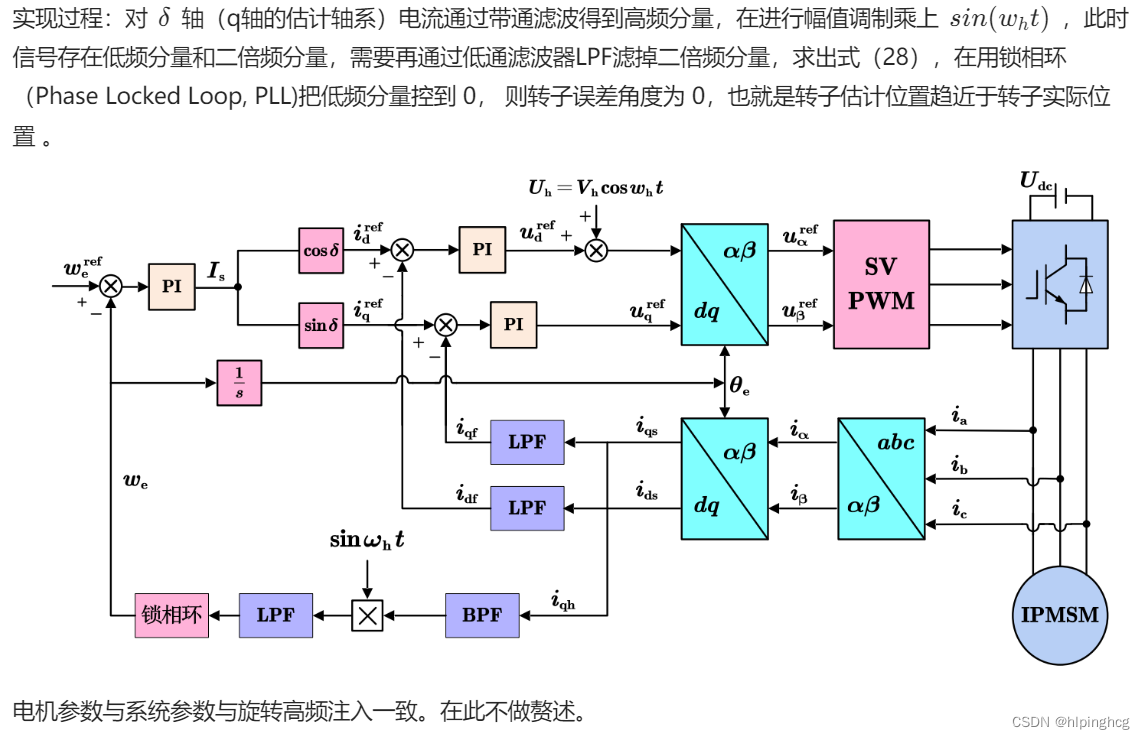
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.2 脉振高频正弦注入法仿真

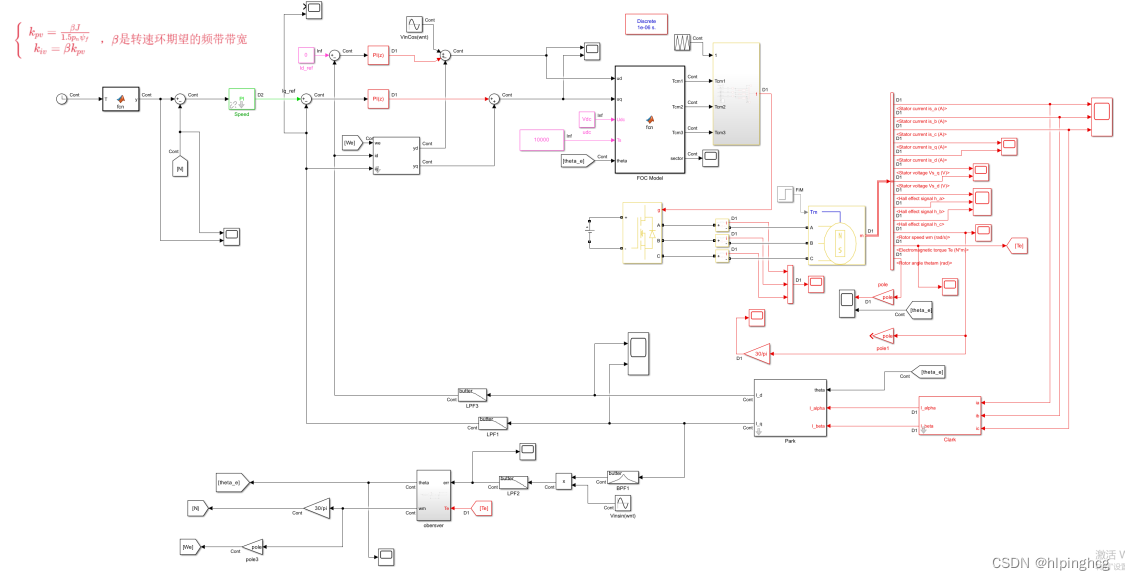
在这里插入图片描述
模型总览：
模型下载地址：永磁同步电机脉振正弦注入初始位置辨识simulink仿真
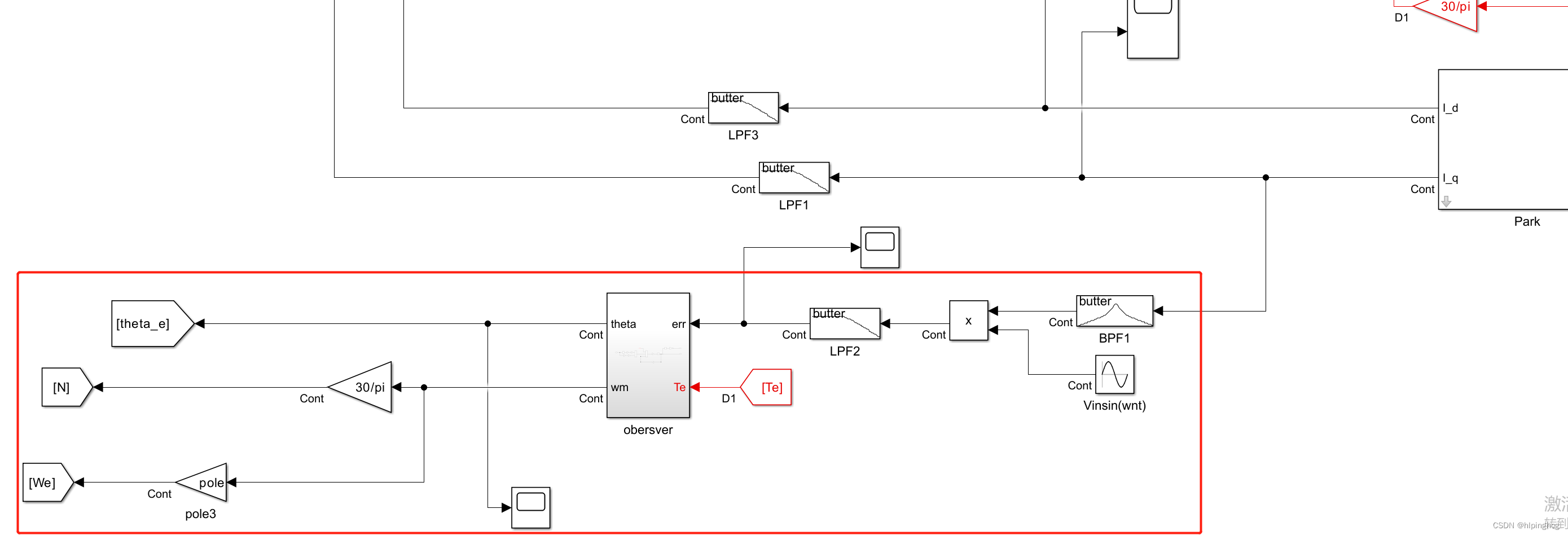
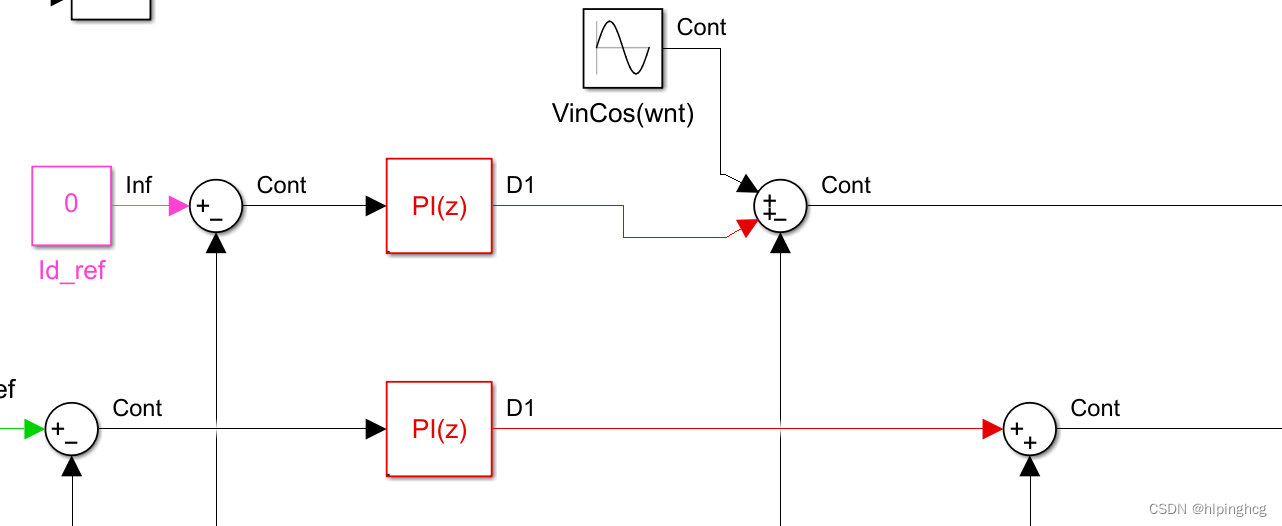
在这里插入图片描述
位置观测部分：
在这里插入图片描述
其中sin参数为：
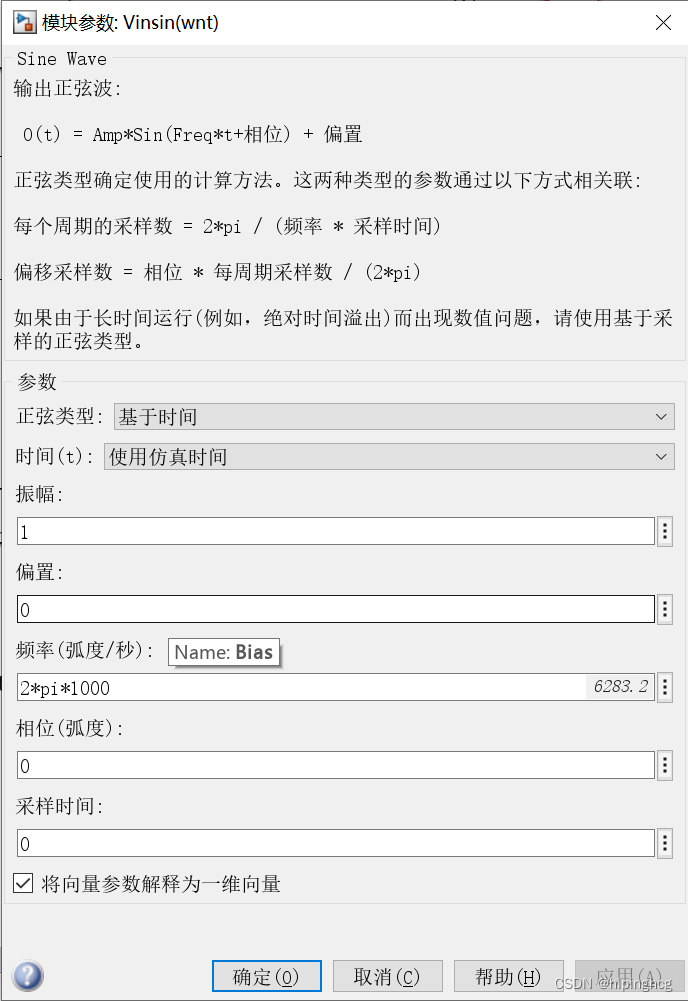
在这里插入图片描述
信号注入：
在这里插入图片描述仿真结果：
给定速度与实际速度
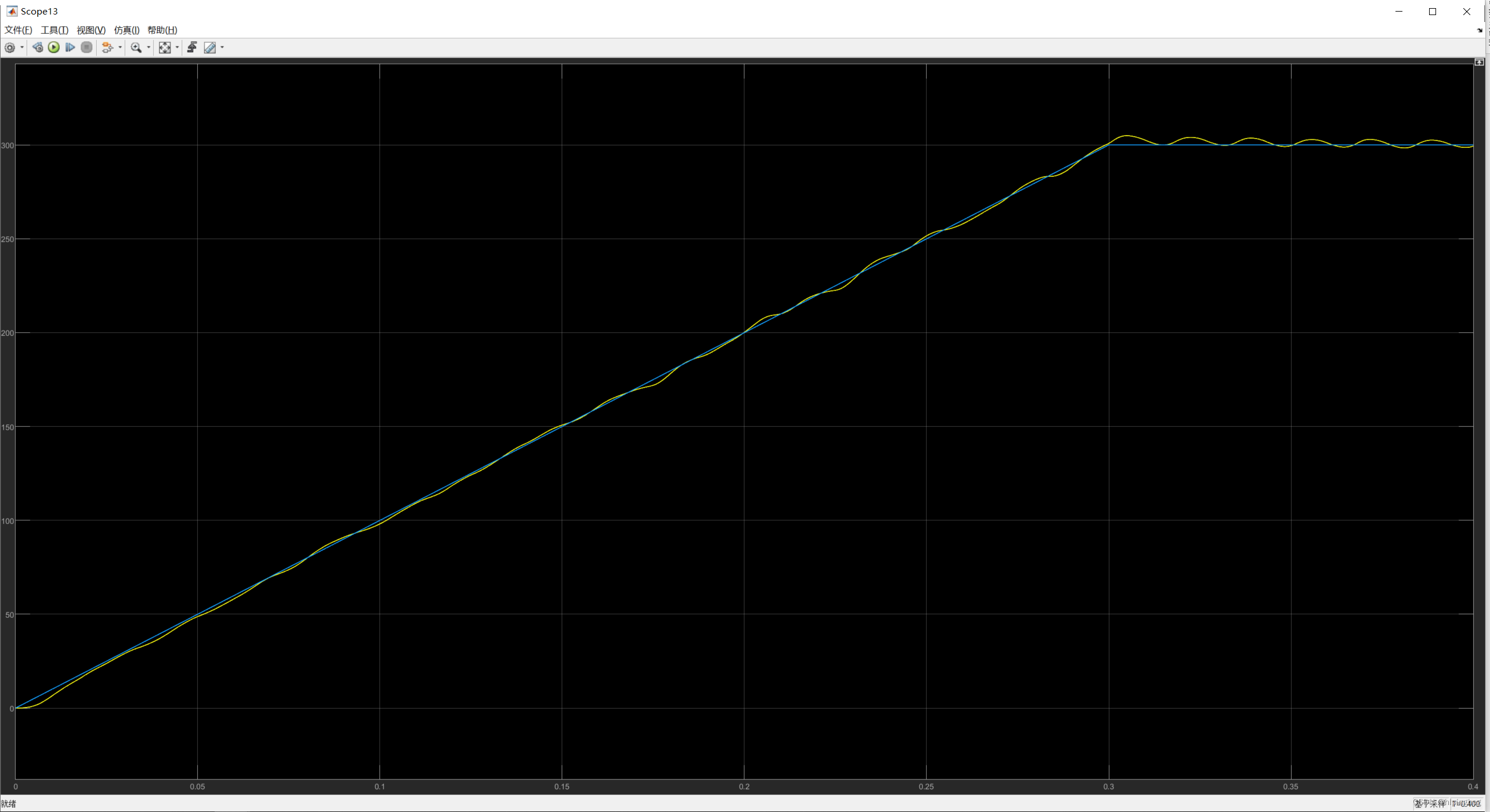
在这里插入图片描述
观测位置与实际位置
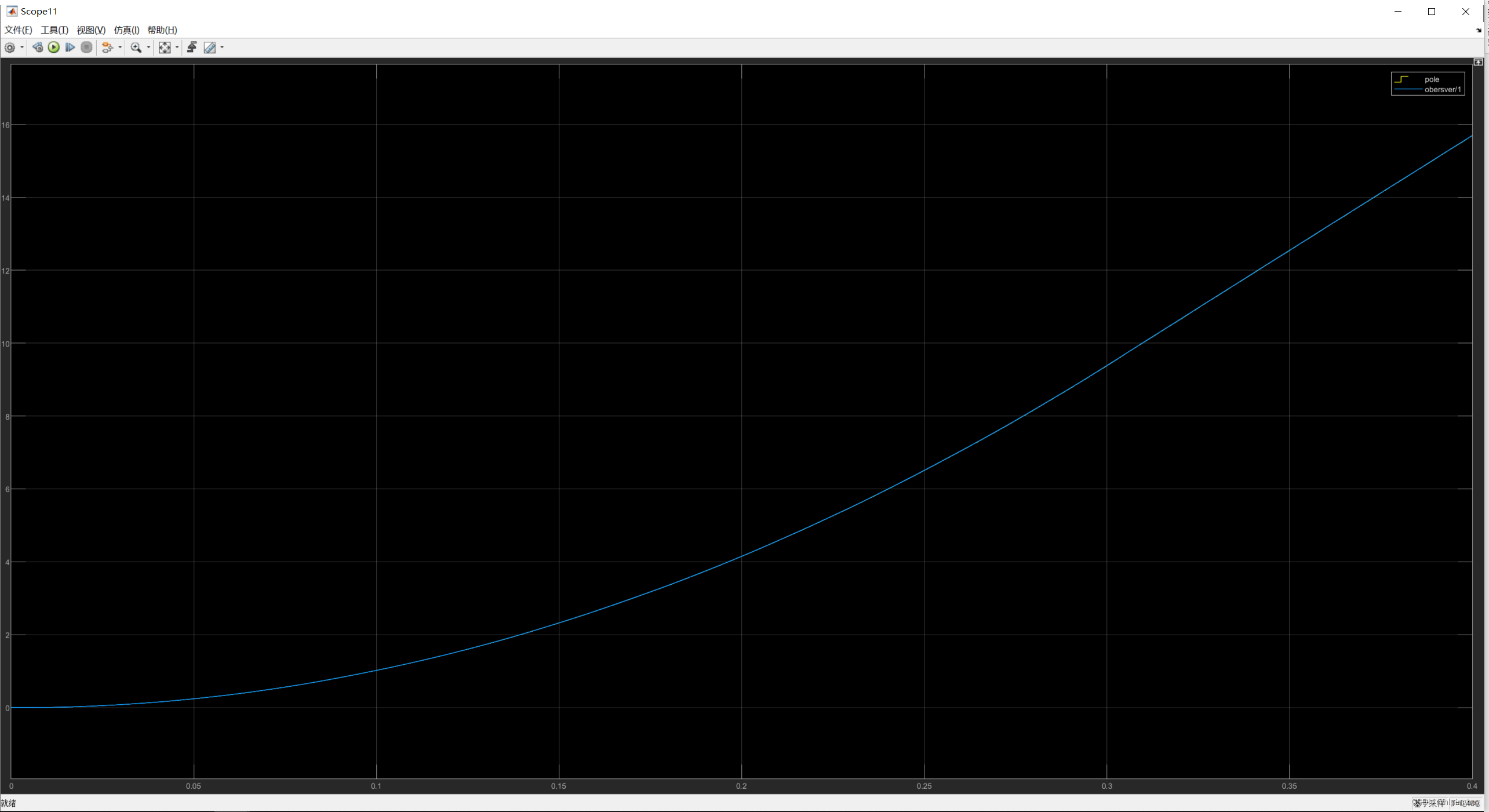
在这里插入图片描述
误差（ 1 0 − 3 10^{-3} 10−3级）
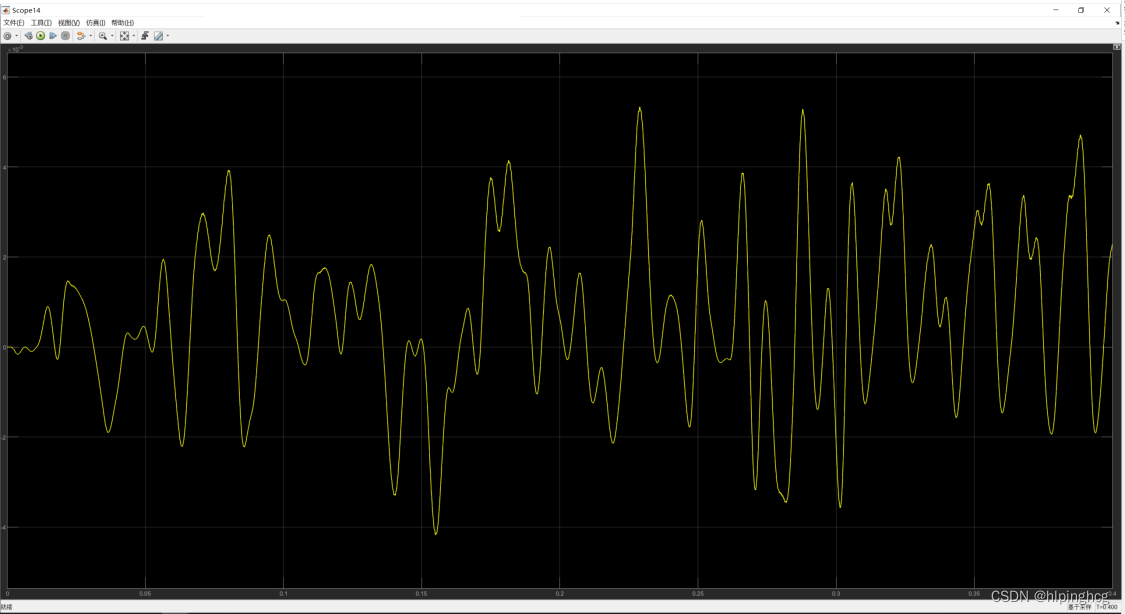
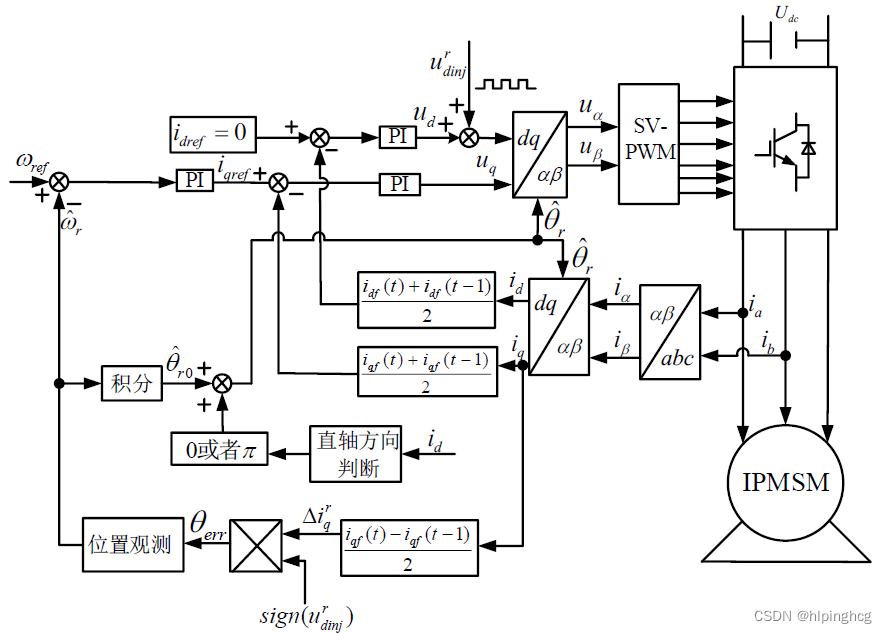
在这里插入图片描述

4、脉振高频方波注入法

4.1 脉振高频方波注入法原理分析

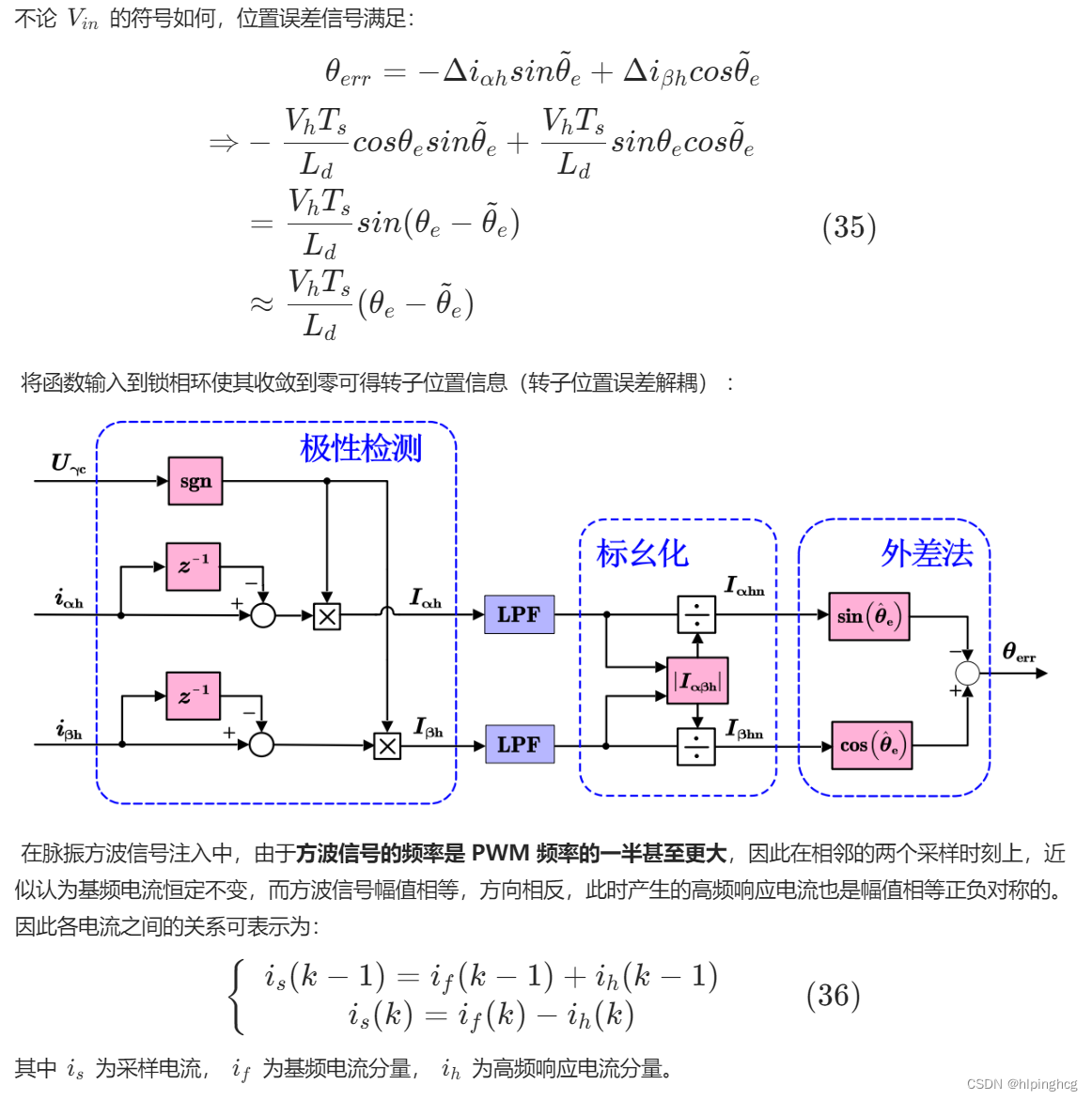
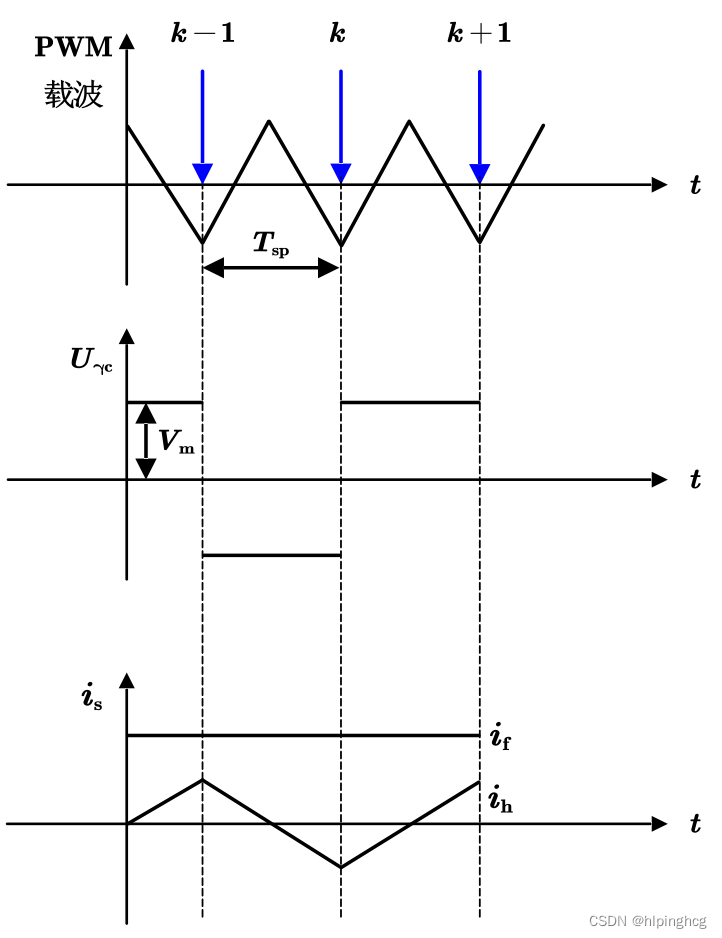
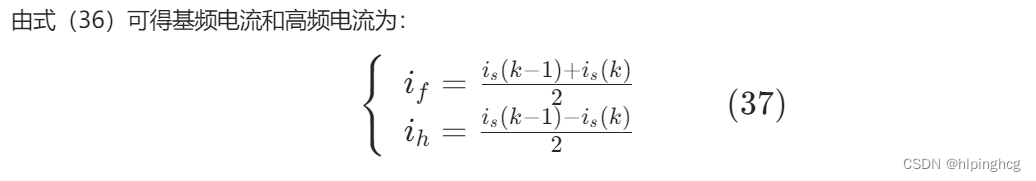
在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述

4.2 脉振高频方波注入法仿真

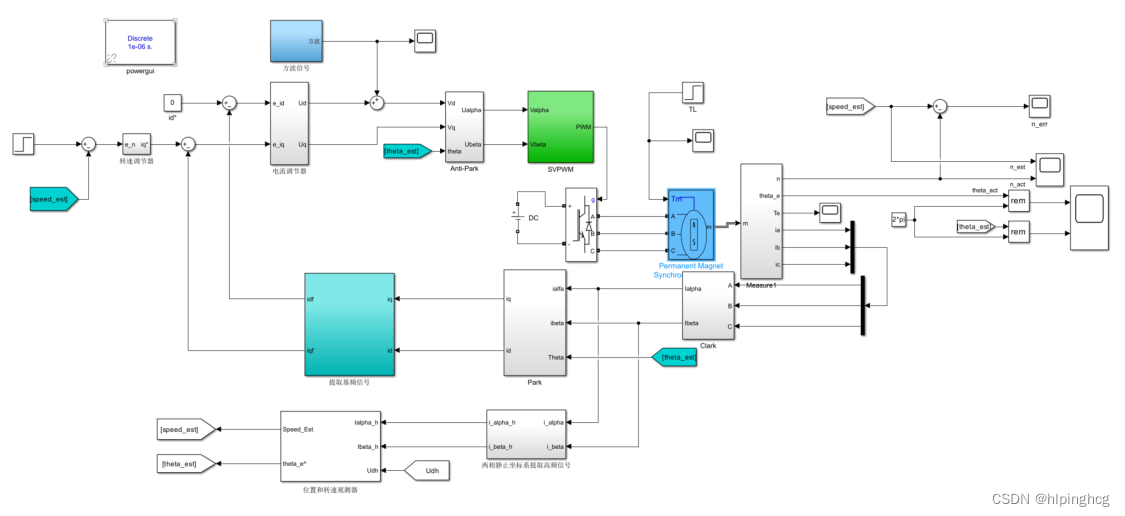
在这里插入图片描述
在这里插入图片描述
电机参数：
在这里插入图片描述
模型总览：
模型下载地址：永磁同步电机脉振方波注入初始位置辨识simulink仿真
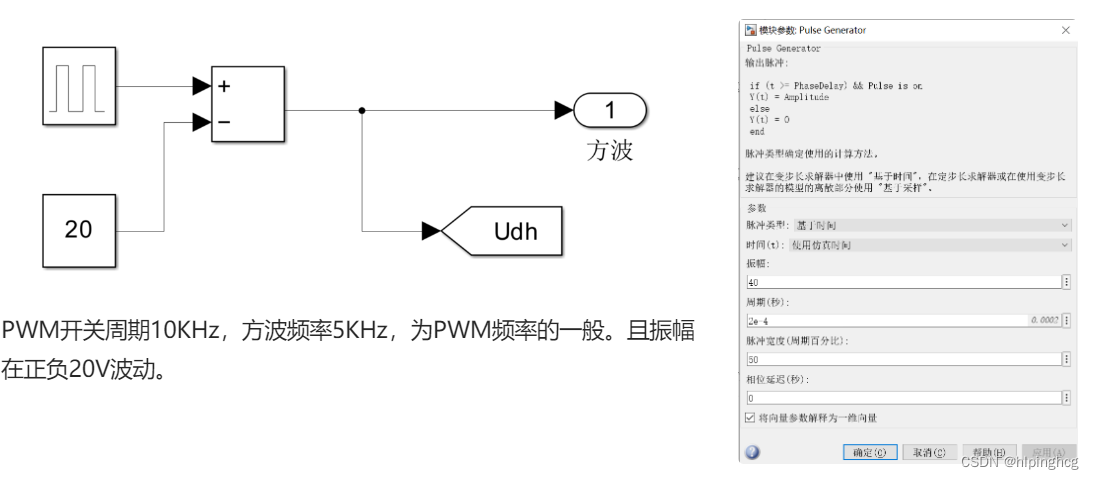
在这里插入图片描述
方波生成模块：
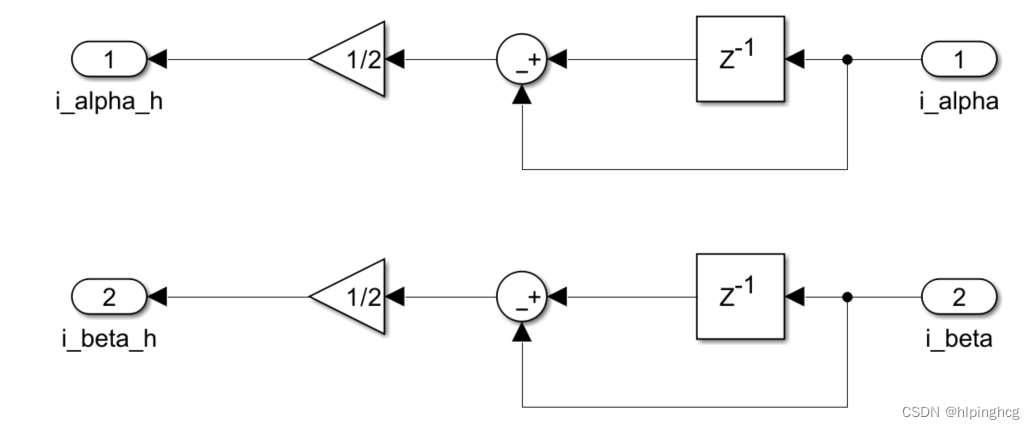
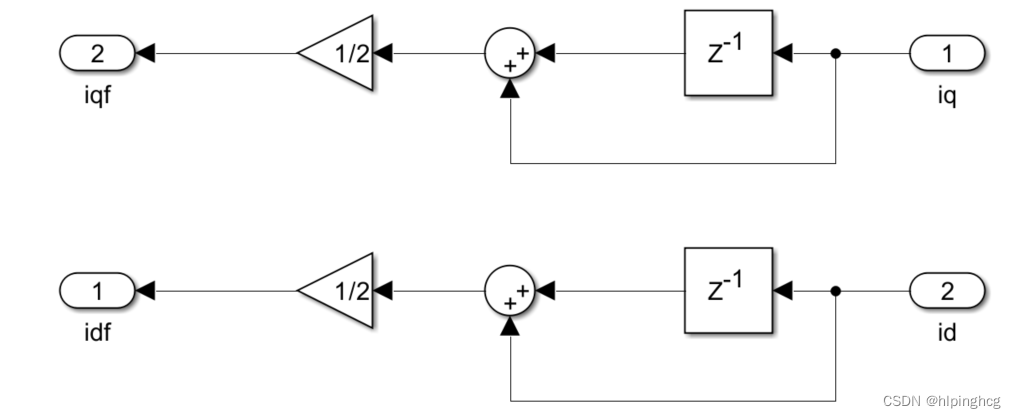在这里插入图片描述
基频提取模块：

在这里插入图片描述高频电流提取模块：
在这里插入图片描述
位置和速度观测模块：
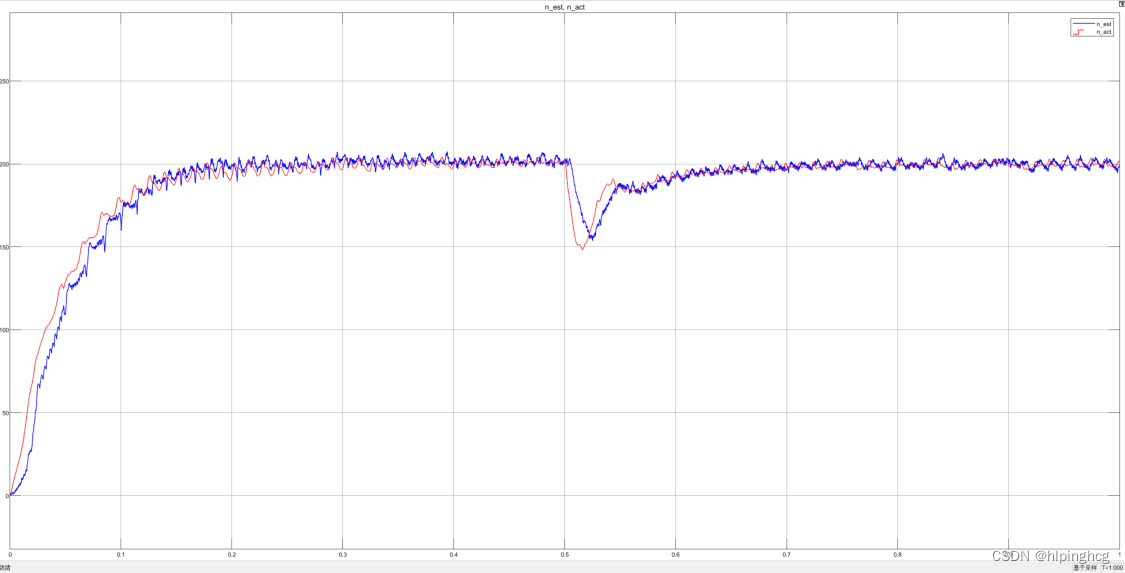
在这里插入图片描述
在这里插入图片描述
观测速度和反馈速度仿真波形：
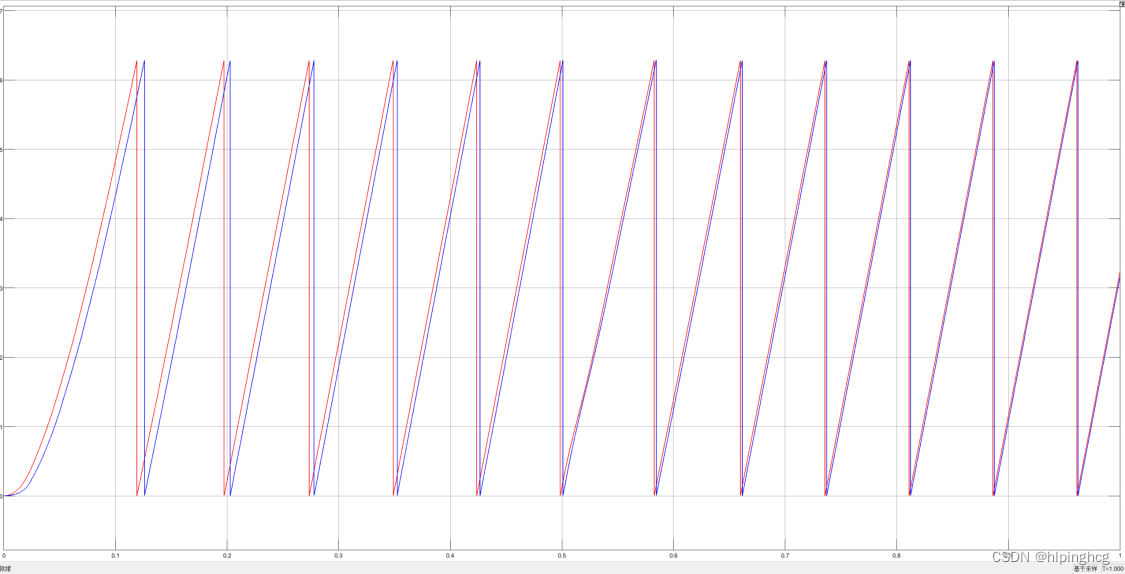
在这里插入图片描述
观测位置与反馈位置仿真波形（电角度）

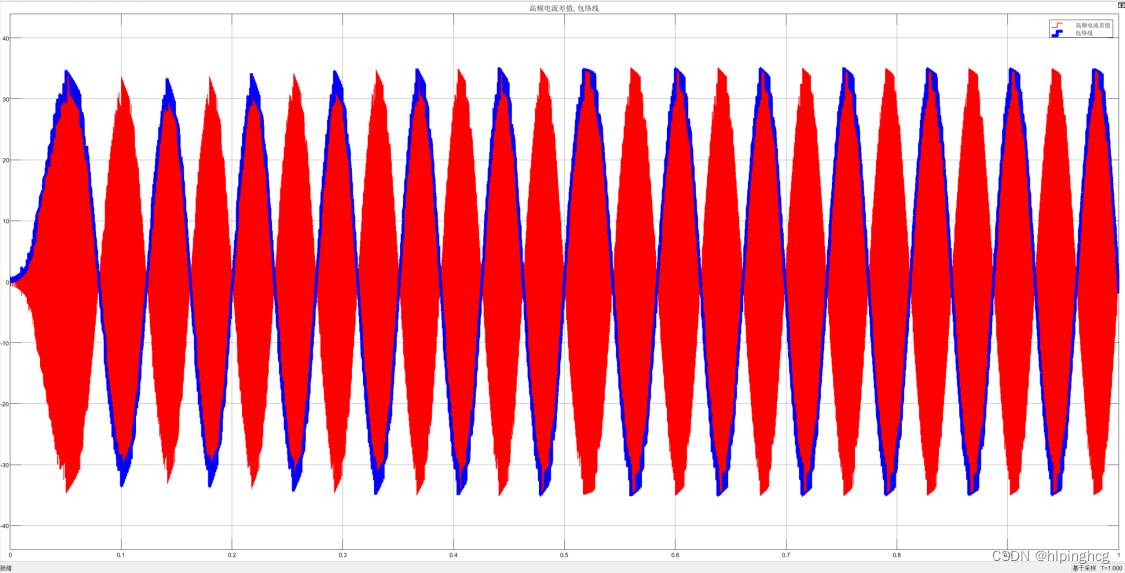
在这里插入图片描述
高频电流差值与包络线波形：

在这里插入图片描述

参考

【1】坐标变换的艺术—PMSM高频注入法公式推导
https://blog.csdn.net/qq_50632468/article/details/124513629
【2】无感FOC之高频注入法——永磁同步电机控制
https://blog.csdn.net/qq_2545470942/article/details/125780928
【3】通俗易懂脉振高频注入法
https://zhuanlan.zhihu.com/p/379999313
【4】基于脉振高频电压信号注入法的PMSM无位置传感器控制原理和仿真
https://blog.csdn.net/weixin_44312889/article/details/121799846
【5】袁雷. 现代永磁同步电机控制原理及 MATLAB 仿真[M]. 北京航空航天大学出版社, 2016.
【6】Yoon Y D, Sul S K, Morimoto S, et al. High-bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J]. IEEE transactions on Industry Applications, 2011, 47(3): 1361-1370.
【7】陈亦斌.基于脉振高频电压注入法的SPMSM无位置传感器控制研究[D].浙江理工大学,2023.DOI:10.27786/d.cnki.gzjlg.2023.001206.
【8】基于旋转高频注入法的永磁同步电机无位置传感器控制
https://blog.csdn.net/weixin_44312889/article/details/121583689
【9】张志良.永磁同步电机高频信号注入初始位置自检测及无传感器运行[D].江苏科技大学,2023.DOI:10.27171/d.cnki.ghdcc.2023.000969.
【10】李鹏飞.电动汽车永磁同步电机无位置传感器复合控制研究[D].安徽工程大学,2023.DOI:10.27763/d.cnki.gahgc.2023.000397.
【11】翟继林. 基于高频信号注入的永磁同步电机无位置传感器控制研究[D].兰州交通大学,2024.DOI:10.27205/d.cnki.gltec.2023.000720.
【12】刘鸿钰. 基于改进的高频方波注入的IPMSM无位置传感器控制研究[D].长安大学,2023.DOI:10.26976/d.cnki.gchau.2023.000315.
【13】基于高频方波电压信号注入的永磁同步电机无传感器控制仿真及其原理介绍：
https://blog.csdn.net/weixin_44312889/article/details/129114282?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-129114282-blog-107780148.235v43pc_blog_bottom_relevance_base2&spm=1001.2101.3001.4242.1&utm_relevant_index=3
【14】李文涛. 基于高频方波注入永磁同步电机无位置传感器控制技术研究[D].中国矿业大学,2021.DOI:10.27623/d.cnki.gzkyu.2020.000444.

这篇关于永磁同步电机高频注入位置观测的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/756637。

相关文章

SpringBoot中@Value注入静态变量方式

SpringBoot中@Value注入静态变量方式

《SpringBoot中@Value注入静态变量方式》SpringBoot中静态变量无法直接用@Value注入,需通过setter方法,@Value(${})从属性文件获取值,@Value(#{})用... 目录项目场景解决方案注解说明1、@Value("${}")使用示例2、@Value("#{}"php
阅读更多...
深入浅出Spring中的@Autowired自动注入的工作原理及实践应用

深入浅出Spring中的@Autowired自动注入的工作原理及实践应用

《深入浅出Spring中的@Autowired自动注入的工作原理及实践应用》在Spring框架的学习旅程中,@Autowired无疑是一个高频出现却又让初学者头疼的注解,它看似简单,却蕴含着Sprin... 目录深入浅出Spring中的@Autowired：自动注入的奥秘什么是依赖注入？@Autowired
阅读更多...
Spring 依赖注入与循环依赖总结

Spring 依赖注入与循环依赖总结

《Spring依赖注入与循环依赖总结》这篇文章给大家介绍Spring依赖注入与循环依赖总结篇,本文通过实例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友参考下吧... 目录1. Spring 三级缓存解决循环依赖1. 创建UserService原始对象2. 将原始对象包装成工
阅读更多...
Spring-DI依赖注入全过程

Spring-DI依赖注入全过程

《Spring-DI依赖注入全过程》SpringDI是核心特性,通过容器管理依赖注入,降低耦合度,实现方式包括组件扫描、构造器/设值/字段注入、自动装配及作用域配置,支持灵活的依赖管理与生命周期控制,... 目录1. 什么是Spring DI？2.Spring如何做的DI3.总结1. 什么是Spring D
阅读更多...
Java Spring的依赖注入理解及@Autowired用法示例详解

Java Spring的依赖注入理解及@Autowired用法示例详解

《JavaSpring的依赖注入理解及@Autowired用法示例详解》文章介绍了Spring依赖注入（DI）的概念、三种实现方式（构造器、Setter、字段注入）,区分了@Autowired（注入... 目录一、什么是依赖注入（DI）？1. 定义2. 举个例子二、依赖注入的几种方式1. 构造器注入（Con
阅读更多...
如何使用Lombok进行spring 注入

如何使用Lombok进行spring 注入

《如何使用Lombok进行spring注入》本文介绍如何用Lombok简化Spring注入,推荐优先使用setter注入,通过注解自动生成getter/setter及构造器,减少冗余代码,提升开发效... Lombok为了开发环境简化代码，好处不用多说。spring 注入方式为2种，构造器注入和setter
阅读更多...
springboot项目打jar制作成镜像并指定配置文件位置方式

springboot项目打jar制作成镜像并指定配置文件位置方式

《springboot项目打jar制作成镜像并指定配置文件位置方式》：本文主要介绍springboot项目打jar制作成镜像并指定配置文件位置方式,具有很好的参考价值,希望对大家有所帮助,如有错误... 目录一、上传jar到服务器二、编写dockerfile三、新建对应配置文件所存放的数据卷目录四、将配置文
阅读更多...
python3如何找到字典的下标index、获取list中指定元素的位置索引

python3如何找到字典的下标index、获取list中指定元素的位置索引

《python3如何找到字典的下标index、获取list中指定元素的位置索引》：本文主要介绍python3如何找到字典的下标index、获取list中指定元素的位置索引问题,具有很好的参考价值,... 目录enumerate()找到字典的下标 index获取list中指定元素的位置索引总结enumerat
阅读更多...
如何更改pycharm缓存路径和虚拟内存分页文件位置(c盘爆红)

如何更改pycharm缓存路径和虚拟内存分页文件位置(c盘爆红)

《如何更改pycharm缓存路径和虚拟内存分页文件位置(c盘爆红)》：本文主要介绍如何更改pycharm缓存路径和虚拟内存分页文件位置(c盘爆红)问题,具有很好的参考价值,希望对大家有所帮助,如有... 目录先在你打算存放的地方建四个文件夹更改这四个路径就可以修改默认虚拟内存分页js文件的位置接下来从高级-
阅读更多...
PyCharm如何更改缓存位置

PyCharm如何更改缓存位置

《PyCharm如何更改缓存位置》：本文主要介绍PyCharm如何更改缓存位置的实现方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录PyCharm更改缓存位置1.打开PyCharm的安装编程目录2.将config、sjsystem、plugins和log的路径
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2