本文主要是介绍【自然语言处理四-从矩阵操作角度看 自注意self attention】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
自然语言处理四-从矩阵操作角度看 自注意self attention
- 从矩阵角度看self attention
- 获取Q K V矩阵
- 注意力分数
- softmax
- 注意力的输出
- 再来分析整体的attention的矩阵操作过程
- 从矩阵操作角度看,self attention如何解决问题的?
- W^q^ W^k^ W^v^这三个矩阵怎么获得?
从矩阵角度看self attention
上一篇文章,【自然语言处理三-自注意self attention】介绍了如何实现selft attention,但没有介绍,为何自注意力就能解决参数扩张、无法并行等问题,仅仅用语言描述太过干涩,从矩阵操作的角度则可以清晰的了解,self attention的运作机制以及它如何解决这些问题的。
首先,还是先给出self attention的整体流程图
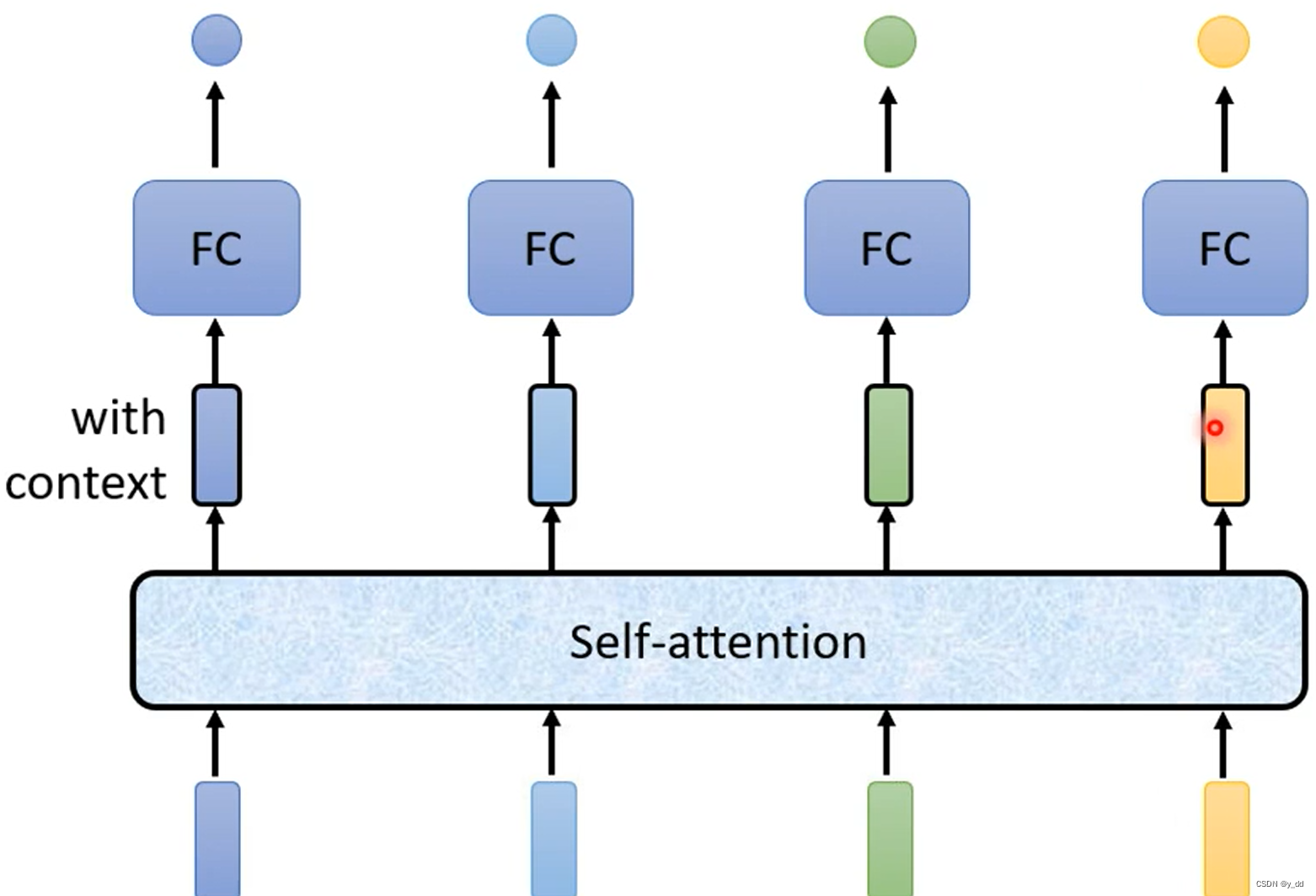
中间这个attention层,从输入到attention层的输出,就是我们是实现的目标,下面是一个简单的图示:
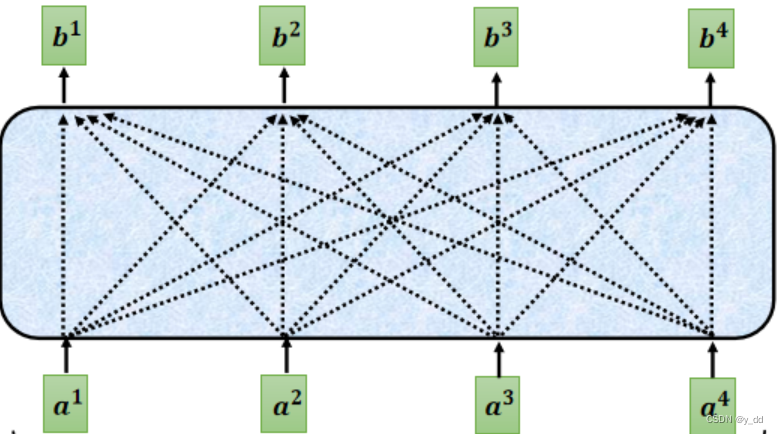
下面我们就从矩阵操作的角度来描述,具体如何实现中间这个self attention层。
获取Q K V矩阵
首先是根据输入乘上矩阵,获取qi,ki,vi
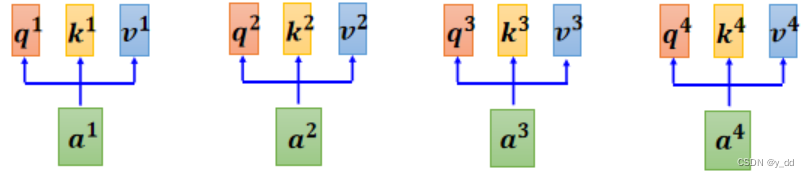
当我们将(ai,…an)整合成一个矩阵的时候,实际上这个操作是这样的:
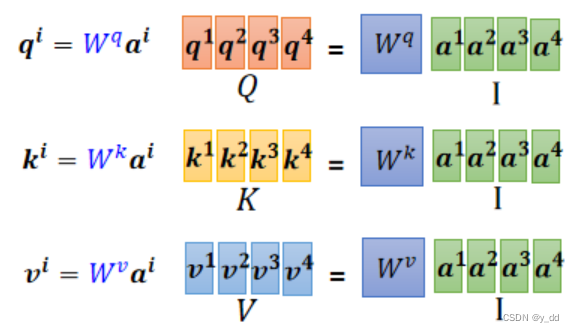
这样我们的Q K V矩阵就是针对整个输入的了。
注意力分数
a1对于ai的注意力分数,是q1和ki的点乘,当然这个点乘操作在上文介绍过,可以有别的方法。
这个过程同样可以合并成一个矩阵操作,如下图:A矩阵中的每一列,就是ai对于其他输入的注意力分数
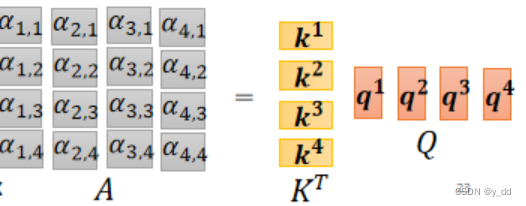
softmax
上述获取的A矩阵执行softmax操作

注意力的输出
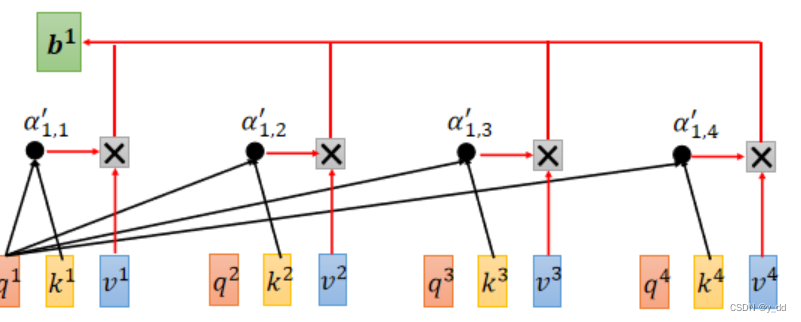
softmax后的注意力分数,与其他输入的vi做乘法操作,获取最终注意力层的一个输出。
这个过程同样可以合并矩阵操作,如下:
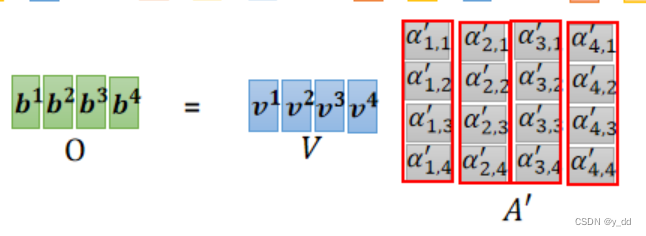
最终的的这个O矩阵就是注意力的输出。
再来分析整体的attention的矩阵操作过程
这个总体的过程,可以用下面更简略的图来表示:
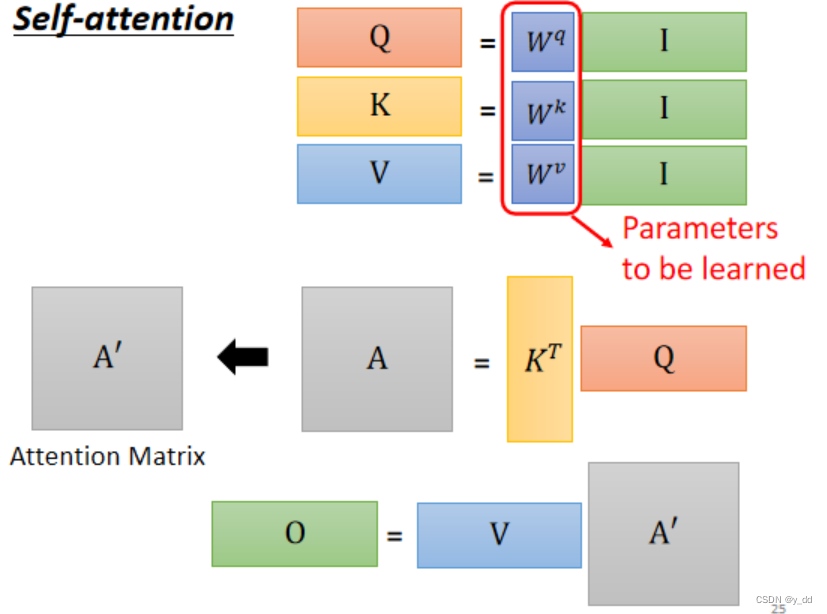
从矩阵操作角度看,self attention如何解决问题的?
1.解决参数可能急剧扩张的问题
我们从上面整体的矩阵操作过程来看,实际上只有三个矩阵Wq Wk Wv的参数需要学习,其他都是经过矩阵运算。
参数不会出现剧增
2.解决无法并行的问题
矩阵对于每个输入的操作,是并行的,不再像seq2seq架构一样,是按照时间步,一步步操作。
3.解决记忆能力的问题
attention的分数是基于全体输入的,且没有经过时间步的传播,因此记忆是基于全句子的,且信息没有丢失
Wq Wk Wv这三个矩阵怎么获得?
从整体流程来看,要实现attention,最关键的就是找到合适的Wq Wk Wv矩阵,那么这三个矩阵是怎么获得的呢?
它们是靠学习获得的,初始化后,经过模型输出,然后经过反向传播,通过调整误差,一步步的精确化了这三个矩阵
这篇关于【自然语言处理四-从矩阵操作角度看 自注意self attention】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




