【动态规划之路径问题】路径条数与带障碍物的路径条数

⭐️前面的话⭐️

本篇文章将介绍动态规划之路径条数的问题，我将通过两道力扣上面的题来介绍使用动态规划来解决路径条数问题以及路上存在障碍物时路径的条数。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年10月17日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《算法》，📚《算法导论》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

⭐️【引入】路径条数问题：62. 不同路径⭐️

🔐题目详情

62. 不同路径

难度中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

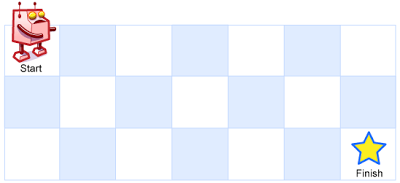
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

💡解题思路

题目的意思是一个机器人从左上角到达右下角的路径数，当然是有限制条件的，条件就是只能向右走或者向下走。

由于本题较为简单，因此将使用本题带你进入动态规划的大门，对于一道问题如果想使用动态规划解决，思考过程如下：

1. 这道题如何使用动态规划，能不能使用动态规划。
2. 如果能够使用动态规划，尝试着定义一个状态。
3. 定义好状态后，尝试去挖掘已知的状态，或者说是确定初始的状态。
4. 确定好初始状态之后，尝试推导状态转移方程。
5. 算法设计完成后，试着分析其时空复杂度。

下面我们以这个步骤来解决这道题。

状态定义: 我们不妨定义$f[i][j]$表示从左上角到位置$(i,j)$的路径条数。

确定初始状态： 当$i=0,j=0$的时候，从原点到达原点的路径数可以认为路径条数为1，即$f[0][0]=1$。

状态转移方程： 一共可以分为三种情况：

1. $i=0,j>0时$，此时到达位置(i,j)只能是左边的位置(i,j-1)移动而来，即$f[i][j]=f[i][j-1]$。
2. $i>0,j=0时$，此时到达位置(i,j)只能是上面的位置(i-1,j)移动而来，即$f[i][j]=f[i-1][j]$。
3. $i>0,j>0时$，此时到达位置(i,j)，可以是上面的位置(i-1,j)移动而来，也可以是左边的位置(i, j-1)移动而来，所以$f[i][j]=f[i-1][j]+f[i][j-1]$。

最终$f[n-1][m-1]$即就是从原点到达右下角的路径条数。

🔑源代码

class Solution {public int uniquePaths(int m, int n) {//状态定义 f[i][j]为起点到(i,j)位置的路径总数int[][] f = new int[n][m];//初始状态 f[0][0] = 1f[0][0] = 1;//状态转移for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (i == 0 && j > 0) f[i][j] = f[i][j - 1];else if (j == 0 && i > 0) f[i][j] = f[i - 1][j];else if (i > 0 && j > 0) f[i][j] = f[i - 1][j] + f[i][j - 1];}}return f[n - 1][m - 1];}
}

$时间复杂度：O(m\ast n)$
$空间复杂度：O(m\ast n)$

🌱总结

如何确定该题可以使用动态规划？
因为到达位置(i,j)的路径数根据题目只能向下或向右走，可以依赖(i-1,j)和(i,j-1)位置进行推导。
如何确定本题的状态定义的？
更多的成分就是猜或者感觉吧，根据上面所说，一个状态依赖前面的状态，可以尝试定义状态$f[i][j]$为到达(i,j)位置的路径条数。
对状态转移的要求是什么？
不重复也不漏掉状态，如果对某个状态重复计算或者缺少某个状态的值的更新，那么得到的结果一定是错误的，需要检查状态转移过程是否正确或者状态定义是否可行。
如何分析动态规划的时空复杂度的？
时间复杂度就是更新状态的次数，有多少个状态更新，时间复杂度就是多少，空间复杂度就是你申请动态规划数组的大小。

⭐️【路上有障碍物】63. 不同路径 II⭐️

🔐题目详情

63. 不同路径 II

难度中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

💡解题思路

这道题想对于上一道题的区别就是路上可能存在障碍物，对于统计的路径条数不能存在障碍物，其实很简单，就是当位置(i,j)没有障碍物的时候，与上一道题一样，位置(i,j)存在障碍物的时候，表示此路不通，将到达(i,j)位置的路径条数为$0$。

据以上分析，我们可以在上一道题的基础之上给出状态定义以及推导的过程：

状态定义: 我们不妨定义$f[i][j]$表示从左上角到位置$(i,j)$的路径条数。

确定初始状态： 当$i=0,j=0$的时候，从原点到达原点的路径数可以认为路径条数为1，即$f[i][j]=1$，如果原点就存在障碍物，路径条数为0，即$f[0][0]=0$。

状态转移方程： 一共可以分为四种情况：

1. 没有遇到障碍物，$i=0,j>0时$，此时到达位置(i,j)只能是左边的位置(i,j-1)移动而来，即$f[i][j]=f[i][j-1]$。
2. 没有遇到障碍物，$i>0,j=0时$，此时到达位置(i,j)只能是上面的位置(i-1,j)移动而来，即$f[i][j]=f[i-1][j]$。
3. 没有遇到障碍物，$i>0,j>0时$，此时到达位置(i,j)，可以是上面的位置(i-1,j)移动而来，也可以是左边的位置(i, j-1)移动而来，所以$f[i][j]=f[i-1][j]+f[i][j-1]$。
4. 遇到障碍物，$f[i][j]=0$。

最终$f[n-1][m-1]$即就是从原点到达右下角的路径条数。

🔑源代码

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {//状态定义 f[i][j]表示到位置(i, j)的路径数int n = obstacleGrid.length;int m = obstacleGrid[0].length;int[][] f = new int[n][m];//初始状态 ob...[0][0] == 1 f[0][0] = 0 否则1f[0][0] = obstacleGrid[0][0] == 1 ? 0 : 1;//状态转移 ob...[i][j] == 1 f[i][j] = 0//其他 i > 0 j > 0 f[i][j] = f[i - 1][j] + f[i][j - 1]//i == 0 j > 0 f[i][j] = f[i][j - 1]//j == 0 i > 0 f[i][j] = f[i - 1][j]for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (obstacleGrid[i][j] != 1) {if (i > 0 && j > 0) f[i][j] = f[i - 1][j] + f[i][j - 1];else if (i == 0 && j > 0) f[i][j] = f[i][j - 1];else if (j == 0 && i > 0) f[i][j] = f[i - 1][j];}}}return f[n - 1][m - 1];}
}

$时间复杂度：O(m\ast n)$
$空间复杂度：O(m\ast n)$

🌱总结

本题相当于上一题，就是存在不可达的路径，遇到障碍物的路径就是不可达路径，我们只需考虑遇到障碍物时就将状态转移的路径条数设置为$0$即可。