本文主要是介绍【动态规划题目讲解】AGC026D - Histogram Coloring,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
[ A G C 026 D ] H i s t o g r a m C o l o r i n g \mathrm{[AGC026D] Histogram\ Coloring} [AGC026D]Histogram Coloring
D e s c r i p t i o n \mathrm{Description} Description
给定 N N N 列的网格,每列高为 h i h_i hi,将每个格子染色成红色或蓝色,使得每个 2 × 2 2\times 2 2×2 的区域都恰好有两个蓝格子和两个红格子,求方案数。
S o l u t i o n \mathrm{Solution} Solution
为了小编书写方便,令 1 1 1 为红, 0 0 0 为蓝(反过来也无所谓)
简化版
思考一下如果 h i h_i hi 全部相等,怎么做呢?(比如说,给个 20 p t s 20\mathrm{pts} 20pts 的部分分)
那么,其实就相当于给定了一个矩形,此时对于矩形的最后一行进行分类讨论:
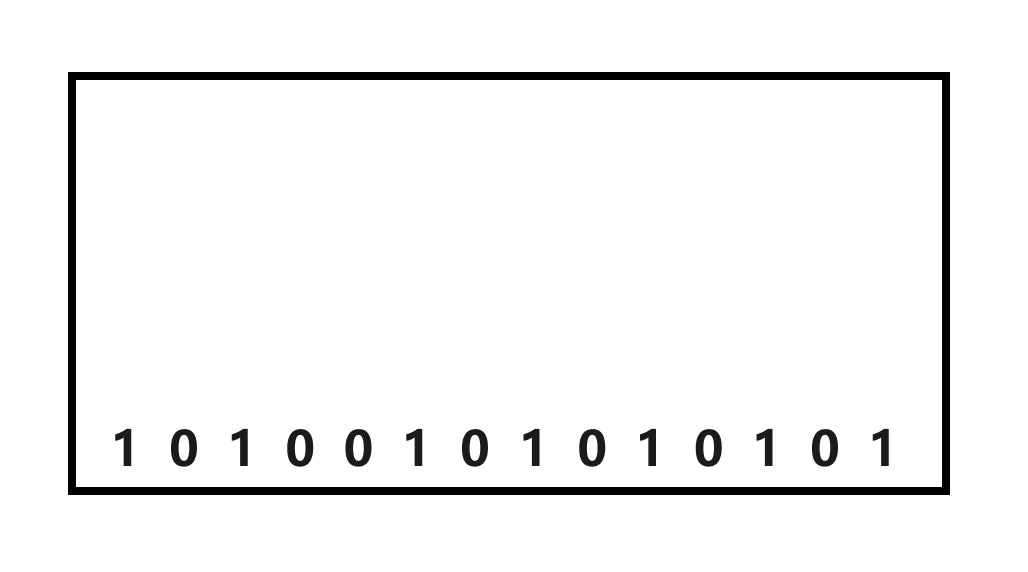
最后一行有 2 2 2 个 0 0 0,那么上一行对应位置只能填 2 2 2 个 1 1 1,对应这别的位置也能相应的填好
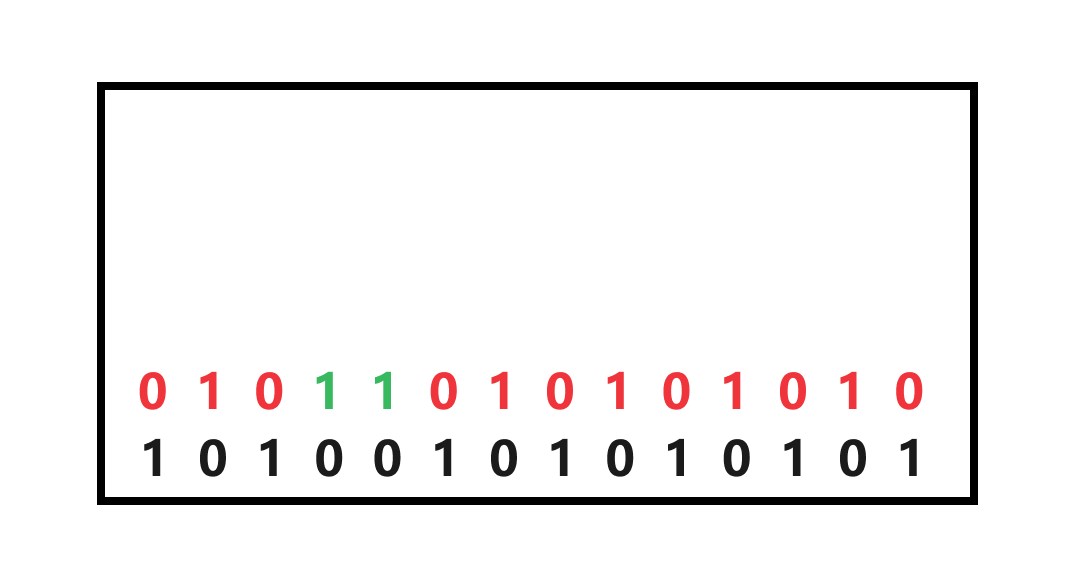
所以,发现其实是一个翻转操作,但是这里的前提是下面有一对连续的 0 0 0,那么才会固定上一行,那如果最后一行是 01 01 01 交替呢?
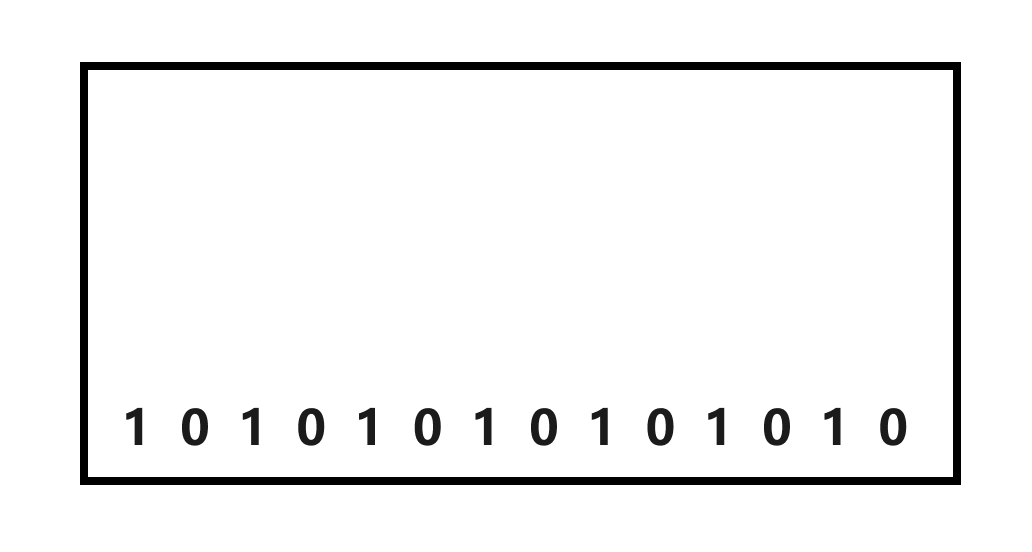
那么,上一行你可以发现有 2 2 2 种填法: 010101 … 010101\dots 010101…, 1010101 … 1010101\dots 1010101…
这样对于每一行都会分成 2 2 2 种,那么最后的方案数应该就是 2 h i 2^{h_i} 2hi(最后一行也是 2 2 2 种)。
而对于第 1 1 1 种情况:底部的状态有 2 n 2^n 2n 种填法,而上面会固定,所以不会再有更多的状态
但是,这 2 2 2 种会算重,即 0101 … 0101\dots 0101… 和 1010 … 1010\dots 1010… 会被算 2 2 2 次,所以最终的方案数为 2 n + 2 h i − 2 2^n+2^{h_i}-2 2n+2hi−2
那么,这是简化版的做法,不过可以借鉴简化版的思路来解决这道问题。
这道题无非就是 h i h_i hi 不相同了,比如说形状如下图所示:( h i h_i hi 可能为 0 0 0)
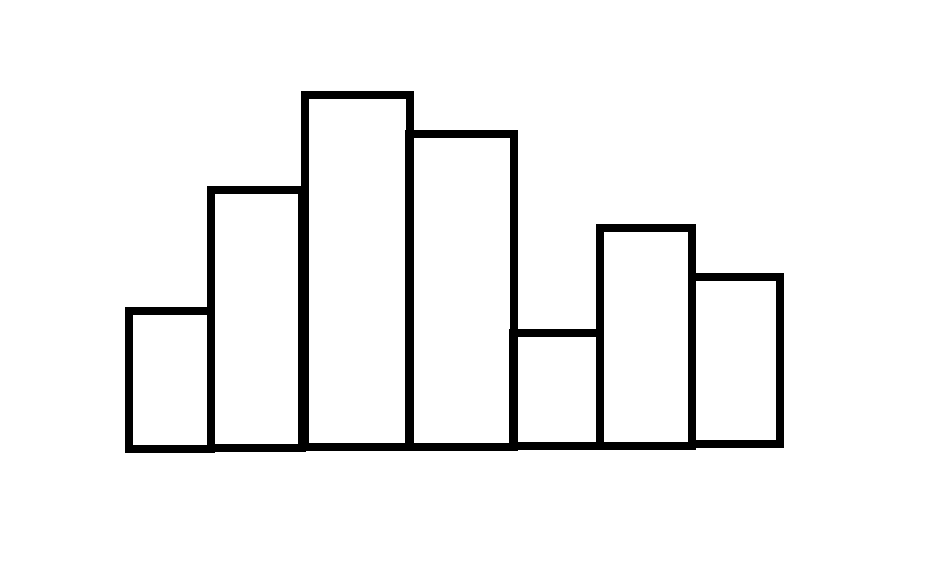
那么,对于这个图,考虑到每次可以划分成一个矩形,考虑子问题,比如说:

只考虑到当前最矮的那个方块,那么下面其实就是一个矩形,然后上面就会分成 2 2 2 个部分,即为两个子问题,那么就可以设计 DP 了!较为自然的想到设 f l , r f_{l,r} fl,r 表示区间 l ∼ r l\sim r l∼r 的方案数,不过只设这些可以吗?其实是不可以的,你会发现还有划分的高度,所以还要存一维高度,以及当前是不是 01 01 01 交替。所以,总结一下,设 f l , r , h , 0 / 1 f_{l,r,h,0/1} fl,r,h,0/1 表示区间 l ∼ r l\sim r l∼r,当前划分高度为 h h h,是/不是 01 01 01 交替。( 0 0 0 表示是, 1 1 1 表示不是)
那么,考虑转移: f l , r , h , 0 = f l , p − 1 , h p , 0 × f p + 1 , r , h p , 0 × 2 h p − h f_{l,r,h,0}=f_{l,p-1,h_p,0}\times f_{p+1,r,h_p,0}\times 2^{h_p-h} fl,r,h,0=fl,p−1,hp,0×fp+1,r,hp,0×2hp−h
其中 p p p 为当前最低方块的位置,即左边的方案数乘右边的方案数,由于划分出的矩形是 01 01 01 交替的,所以每行都有 2 2 2 种,总共就是 2 h p − h 2^{h_p-h} 2hp−h 种。
下面考虑不是 01 01 01 交替的转移:
如果左侧是 01 01 01 交替,右侧是 01 01 01 交替,那么总共有 6 6 6 种,因为中间 p p p 位置要想让区间 l ∼ r l\sim r l∼r 不是 01 01 01 交替,那么必须和左侧或右侧中有一个是相等的。(这里就不一一列举了)
如果左侧 01 01 01 交替,右侧不是 01 01 01 交替,那么左侧可以是 01 01 01 或 10 10 10, p p p 位置有 2 2 2 种选择,所以是 4 4 4 种。
如果左侧不是 01 01 01 交替,右侧是 01 01 01 交替,那么同理可得是 4 4 4 种。
如果左侧和右侧都不是 01 01 01 交替,那么只能 p p p 点取 0 / 1 0/1 0/1,是 2 2 2 种。
综上所述:令 l 0 = f l , p − 1 , h p , 0 , l 1 = f l , p − 1 , h p , 1 , r 0 = f p + 1 , r , h p , 0 , r 1 = f p + 1 , r , h p , 1 l_0=f_{l,p-1,h_p,0},l_1=f_{l,p-1,h_p,1},r_0=f_{p+1,r,h_p,0},r_1=f_{p+1,r,h_p,1} l0=fl,p−1,hp,0,l1=fl,p−1,hp,1,r0=fp+1,r,hp,0,r1=fp+1,r,hp,1
则, f l , r , h , 1 = 6 l 0 r 0 + 4 l 0 r 1 + 4 l 1 r 0 + 2 l 1 r 1 f_{l,r,h,1}=6l_0r_0+4l_0r_1+4l_1r_0+2l_1r_1 fl,r,h,1=6l0r0+4l0r1+4l1r0+2l1r1
A c c p e t e d C o d e \mathrm{Accpeted\ Code} Accpeted Code
#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;
typedef unsigned long long ull;const int SIZE = 1e2 + 10, MOD = 1e9 + 7;int N;
int H[SIZE];int ksm(int a, int b, int p)
{int Result = 1;while (b){if (b & 1) Result = Result * a % p;a = a * a % p;b >>= 1;}return Result;
}
int DP(int l, int r, int h, int k)
{if (l > r) return 1;if (l == r) return k ? 0 : ksm(2, H[l] - h, MOD);int Min = 1e18, P;for (int i = l; i <= r; i ++)if (H[i] < Min) Min = H[i], P = i;if (!k) return DP(l, P - 1, H[P], 0) * DP(P + 1, r, H[P], 0) % MOD * ksm(2, H[P] - h, MOD) % MOD;if (P == l) return 2 * (DP(P + 1, r, H[P], 0) + DP(P + 1, r, H[P], 1)) % MOD;if (P == r) return 2 * (DP(l, P - 1, H[P], 0) + DP(l, P - 1, H[P], 1)) % MOD;int L0 = DP(l, P - 1, H[P], 0), L1 = DP(l, P - 1, H[P], 1), R0 = DP(P + 1, r, H[P], 0), R1 = DP(P + 1, r, H[P], 1);return (6 * L0 % MOD * R0 % MOD + 4 * L1 * R0 % MOD + 4 * L0 * R1 % MOD + 2 * L1 * R1 % MOD) % MOD;
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> N;for (int i = 1; i <= N; i ++)cin >> H[i];cout << (DP(1, N, 0, 0) + DP(1, N, 0, 1)) % MOD << endl;return 0;
}
这篇关于【动态规划题目讲解】AGC026D - Histogram Coloring的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





