coloring专题

193 - Graph Coloring（DFS）

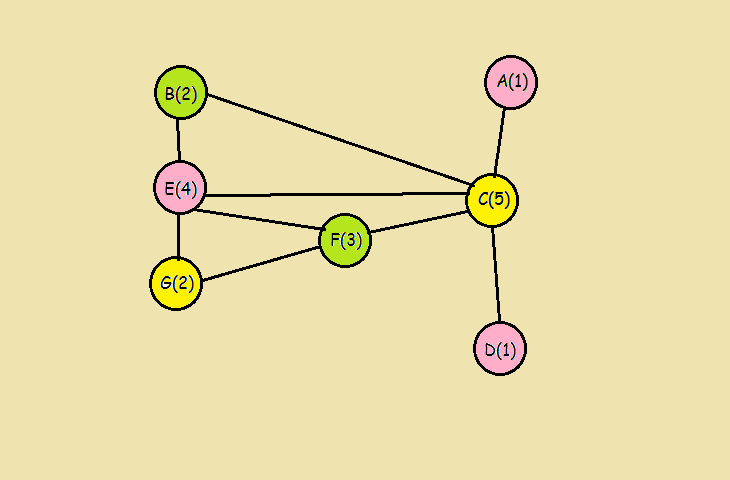
题目：193 - Graph Coloring 题目大意：给出一个图，图里面有点和边，要求相邻的点不可以都是黑色的，问怎样上色黑色的点最多的，给出字典序最大的那种组合情况。解题思路：dfs每个点是黑是白，将黑的点保存记录下来，然后下次再试探某个点是黑点的时候，就看看这个点和之前的那些点有没有相邻，相邻就表示这个点不是黑点。每个试探的点只需要是这个点之后的点就可以了，因为前面的点已经

Codeforces CROC 2016 - Final Round B. Graph Coloring【2-SAT、二分图染色】

B. Graph Coloring 题意有 n n n 个节点和 m m m 条边，起初每条边都有具有颜色 0 0 0 或 1 1 1 其中一种，可以选择一个节点，并将所有与这个点直接相连的边的颜色都翻转，问最少需要选择多少节点才能使所有边的颜色都一样？思路我们可以先枚举最终颜色为 0 0 0 或 1 1 1，那么对于一条边：如果其初始颜色与最终颜色不同，那么这条

牛客国庆集训派对Day3 J Graph Coloring I

题目：点击打开链接题意：判断一个图是否能用两种颜色染色，满足相邻点的颜色不同。分析：可以直接对图进行染色，如果发现当前点的颜色与已经染色的相邻点相同，则存在奇环（环山点的总数为奇数）。也可以判断是否为二分图，因为二分图与奇环互斥。证明：假设二分图中的环是奇数环。设一个环，x1，x2，x3，，，，x(2*k-1)，k>=1且为整数。相邻两点有边连接，x1与x(2*k-1)相连。由

C#，图论与图算法，图着色问题（Graph Coloring）的威尔士-鲍威尔（Welch Powell Algorithm）算法与源代码

Welsh, D.J.A. and Powell, M.B. (1967) An Upper Bound for the Chromatic Number of a Graph and Its Application to Timetabling Problems. 《The Computer Journal》, 10, 85-86. 《The Computer Journal》

1154 Vertex Coloring (25 分)

版本2 图的深搜 #include <cstdio>#include <iostream>#include <vector>#include <cstring>#include <queue> #include <unordered_set>#include <algorithm>using namespace std;const int N = 1e4+5;vector<i

【动态规划题目讲解】AGC026D - Histogram Coloring

[ A G C 026 D ] H i s t o g r a m C o l o r i n g \mathrm{[AGC026D] Histogram\ Coloring} [AGC026D]Histogram Coloring D e s c r i p t i o n \mathrm{Description} Description 给定 N N N 列的网格，每列高为 h i

Dreamoon Likes Coloring CodeForces - 1330C（贪心+思维）

Dreamoon likes coloring cells very much. There is a row of n cells. Initially, all cells are empty (don’t contain any color). Cells are numbered from 1 to n. You are given an integer m and m integer

ARC073 ：Ball Coloring （球染色） UPC-2018山东冬令营（贪心）

球染色时间限制: 2 Sec 内存限制: 512 MB 提交: 66 解决: 22 [ 提交][ 状态][ 讨论版] 题目描述有n组球，每组有两个球，权值分别为xi, yi。你需要对每组球染色，一个染成红色，一个染成蓝色。 Rmax, Rmin, Bmax, Bmin分别表示红色的球中权值最大的，红色的球中权值最小的，蓝色的球中权值最大的，蓝色的球中权值最小

Codeforces Round #631 (Div. 2) - Thanks, Denis aramis Shitov! C. Dreamoon Likes Coloring（贪心+思维）

题目链接 #include<bits/stdc++.h>using namespace std;typedef long long ll;const int maxn=1e5+5;int p[maxn];int ans[maxn];int main(){int n,m;ll sum=0;scanf("%d %d",&n,&m);int cnt=n;for(int i=1;i<=

CF1551B Wonderful Coloring

文章目录 CF1551B1 Wonderful Coloring - 1CF1551B2 Wonderful Coloring - 2 CF1551B1 Wonderful Coloring - 1 题目描述 AC代码： #include<bits/stdc++.h>using namespace std;long long num,ans,n;int a[30];s

[ABC294Ex] K-Coloring

题目传送门引属于一眼题,不看时间限制 8 s 8s 8s 容易被诈骗解法简单容斥大概式子就是 ∑ ( − 1 ) M ∗ K ∣ S ∣ \sum(-1)^{M}*K^{|S|} ∑(−1)M∗K∣S∣ , M M M 为边集的大小， ∣ S ∣ |S| ∣S∣ 为联通块的数量那么我们就有空间复杂度： O ( 2 N ) = 1 e 9 O(2^N) =1e9

unity填色绘画游戏Drawing Coloring Extra Edition

unity填色绘画游戏Drawing Coloring Extra Edition 、下载地址： https://item.taobao.com/item.htm?spm=0.7095261.0.0.2e611debLdF3mf&id=576153069662 posted on 2018-08-26 17:43 jiahuafu 阅读(...) 评论(...