opengles 顶点坐标变换常用的矩阵(九)

本文主要是介绍opengles 顶点坐标变换常用的矩阵(九)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

前言

本文主要介绍 opengles 常用的 model 矩阵（包括用于位移， 缩放，旋转的4x4 矩阵）,以及使用第三方的封装库生成 opengles 的 model ，view, projection(模型，视图，投影)矩阵。
软硬件环境：
硬件：PC
软件：ubuntu22.04 opengles3.0

---

一、opengles 常用的模型矩阵

1. 单位矩阵

在顶点 shader 语句中，如果没有指定 model 矩阵，那么就会使用默认的 model 矩阵，默认的 model 矩阵是一个单位矩阵
在OpenGLES中，由于某些原因我们通常使用4×4的变换矩阵，而其中最重要的原因就是大部分的向量都是4分量的。我们能想到的最简单的变换矩阵就是单位矩阵(Identity Matrix)。单位矩阵是一个除了对角线以外都是0的N×N矩阵。在下式中可以看到，这种变换矩阵使一个向量完全不变

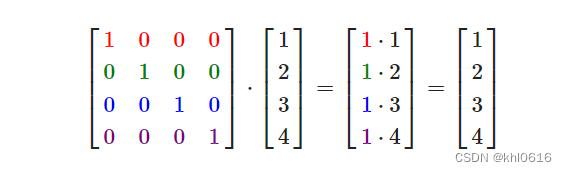
2. 缩放矩阵

我们从单位矩阵了解到，每个对角线元素会分别与向量的对应元素相乘。如果我们把1变为3会怎样？这样子的话，我们就把向量的每个元素乘以3了，这事实上就把向量缩放3倍。如果我们把缩放变量表示为(S1,S2,S3)，我们可以为任意向量(x,y,z)定义一个缩放矩阵：

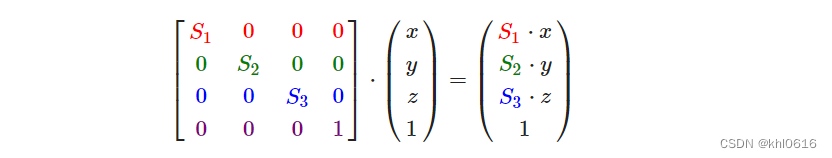
3. 位移矩阵

和缩放矩阵一样，在4×4矩阵上有几个特别的位置用来执行特定的操作，对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz)，我们就能把位移矩阵定义为：

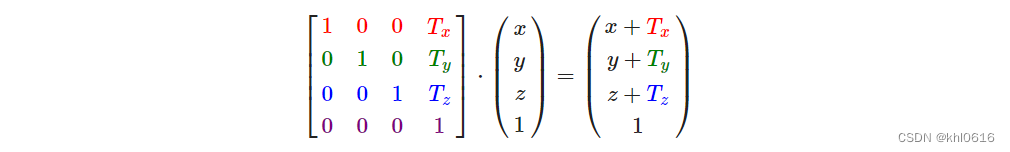
4. 旋转矩阵

旋转矩阵在3D空间中每个单位轴都有不同定义，旋转角度用θ表示：

二、第三方矩阵数学库

1. glm

• glm是一个C++数学库，用于进行OpenGL开发时常用的数学计算，例如向量、矩阵、四元数等。它提供了许多方便的函数和工具，可以简化在OpenGL程序中进行数学计算的过程。
• 在OpenGL开发中，通常使用glm来进行模型变换、投影变换、法线变换等数学运算。glm库中包含了许多常用的数学函数和数据结构，使得开发者能够更轻松地处理3D图形编程中的数学问题。例如，您可以使用glm::mat4表示4x4的矩阵，glm::vec3表示三维向量，glm::quat表示四元数等。glm还提供了丰富的数学函数，如矩阵乘法、向量点乘、向量叉乘等，以及各种变换函数，如旋转、平移、缩放等。
• 在使用 glm之前，您需要包含适当的 glm 头文件（glm 库就是一个头文件，没有.so
  库），通常情况下，您可以直接在代码中使用glm提供的函数和数据结构，从而简化数学计算的过程。

1.1 ubuntu 上安装 glm 库

在ubuntu 上可以通过 sudo apt intstall libglm-dev 命令来安装 glm 库文件，如下图所示

安装成功后，在 /usr/include/glm/ 目录下就可以看到 glm 相关的头文件了，如下图所示

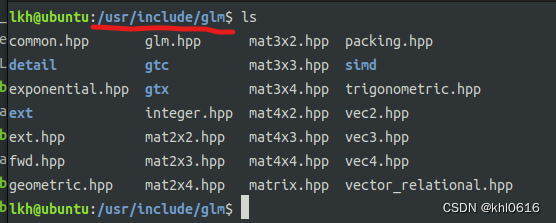
1.2 glm 使用实例

如下是几个使用 glm 生成 opengles 相关的4x4 model ，view, projection 矩阵的实例

1.2.1 生成一个沿Y轴旋转45度的4x4旋转矩阵, 代码实例如下

test_glm1.cpp

#include <iostream>
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>int main() {float angleY = 45.0f; // 45度角度glm::mat4 rotationMatrix = glm::mat4(1.0f); // 初始化为单位矩阵// 绕Y轴旋转45度rotationMatrix = glm::rotate(rotationMatrix, glm::radians(angleY), glm::vec3(0.0f, 1.0f, 0.0f));// 打印结果std::cout << "Rotation Matrix:" << std::endl;for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {std::cout << rotationMatrix[i][j] << " ";}std::cout << std::endl;}return 0;
}

编译命令：g++ test_glm1.cpp -o test_glm1
生成结果：执行 ./test_glm1 命令打印生成的矩阵结果如下：

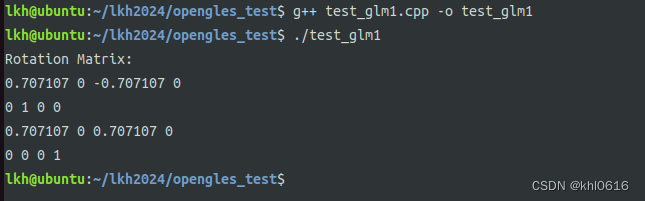
其中这个0.707107 就是 cos45° 和 sin45° 的值

1.2.2 生成一个将物体移到到Z轴正方向坐标为5处的4x4 view视图矩阵, 代码实例如下

test_glm2.cpp

#include <iostream>
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>int main() {glm::mat4 viewMatrix = glm::mat4(1.0f); // 初始化为单位矩阵// 将视点移动到 Z 轴 5 处viewMatrix = glm::translate(viewMatrix, glm::vec3(0.0f, 0.0f, -5.0f));// 打印结果std::cout << "View Matrix:" << std::

这篇关于opengles 顶点坐标变换常用的矩阵(九)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---