本文主要是介绍7分钟0基础彻底理解常用数据压缩原理---哈夫曼编码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
如果你之前没有做过数据压缩,或者想要了解数据压缩的原理,那么这编文章将会帮到你。这编文章将会带你彻底了解哈夫曼编码原理,这种编码方式常用作的图片无损压缩,和ZIP的等压缩存储。
思考,计算机的存储与解析获取
这里有一组数据为1, 3,4,5,6,1,4,3,5. 单位为字节,把他们存起来。那么二进制就是1,11,100,101,110,1,100,11, 101. 但是计算机存储的时候,他们每个数据占8个“格子” ,即为**00000001, 00000011,00000100,00000101,00000110,
00000001,00000100, 00000011,00000101.**真正存储的时候是没有分割区分的,数据都是放在一起的。000000010000001100000100000001010000011000000001000001000000001100000101 。那么是怎么识别获取的数据的呢? 读取的时候,每8个位置作为一个数据读取,如果是int类型,一般都是32位,即每32位作为一个数据。
即为
可见,前缀为00000这部分是无效数据,无疑会浪费了很大一部分空间。这种存储编码被成为定长编码。这是为什么会这样子存储?因为如果不固定长度,计算机就不会知道读的数据是什么。举个例子,1和3放在在一起为111,如果不固定位数,可能识别为3和1(11,1)也可以识别为1和3(1,11),甚至全部读取为一个数字为7(111)
那么有没有一种存储方式可以按需节约来存储呢?答案是有!
树的知识
我们先回顾下关于树的知识点,方便我们理解下面的内容。
叶子结点
叶子结点是指一个树形结构中,没有任何子结点的节点,也就是说它是树结构的最底层节点。

什么是度?
当前结点的最大的子节点数目。也就是分支的数目。

如图,A的度为2, B的度为2. 而叶子结点的度为0. 由此可见,二叉树结点的最大的度为2.最小为0.
什么是路径,路径长度
路径: 是指从树中一个节点到另一个节点的分支所构成的路线。
路径长度: 从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度。

例如:A到F的路径长度为2。A到H的路径长度为3
什么是权值
权值就是某个结点存储的数据的值。如下图,H结点存了一个数据是100,那么久叫他的权值为100

什么是带权路径长度
权路径长度是指根结点到某的结点的路径的长度和该结点的权值相乘的结果。
如上图, 根结点A到H的路径为3, 而H结点的权值为100,那么他的带权路径长度为3*100=300
哈夫曼编码
我们不急着怎么看他的定义,先通过例子去理解。
现在有个一串字母"ACCCCCABDDD",按照下面方式将它进行特殊存储。
下面是字符对应二进制表格
| 字符 | 二进制 |
|---|---|
| A | 01000001 |
| B | 01000010 |
| C | 01000011 |
| D | 01000100 |
第一步,将数据进行节约存储。
为了节约数据空间,我们把前面可以理解为多余的部分空间去掉,做个映射表,即为
| 字符 | 二进制 |
|---|---|
| A | 1 |
| B | 10 |
| C | 11 |
| D | 100 |
第二步,统计每一个字符的出现个数
| 字符 | 出现个数 |
|---|---|
| A | 1 |
| B | 2 |
| C | 5 |
| D | 3 |
第三步,按“出现个数”进行排序
| 字符 | 出现个数 |
|---|---|
| C | 5 |
| D | 3 |
| B | 2 |
| A | 1 |
第四步,构建带权值的二叉树
将“出现个数”作为父结点权值(具体规则看下面步骤), 将字符二进制数据作为叶子结点权值,构建二叉树。将权值越大的,距离根节点越近,最大权值带权路径最短,以此例推。(如果忘记权的概念,请到上面重复阅读)
(1)首先把最小的两个权值的作为叶子节点 ,出现次数大的在左边, 构建一个二叉树。如下图
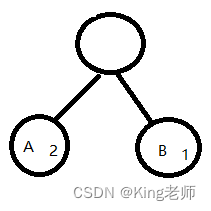
(2)将这个新组成的二叉树他的父节点求权值,将A和B的权值相加,得到 3,如下
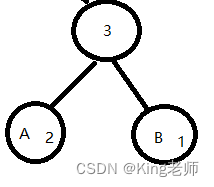
(3)将比A和B最近的数据进行构建新组合二叉树,刚刚好比A和B大的数据是D,将D与A,B的父节点,作为同一层构建二叉树,如下。
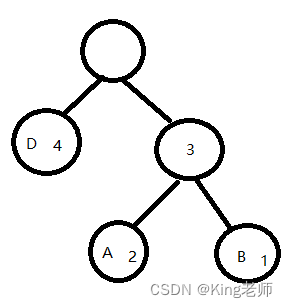
然后继续求顶部根节点的权值,将D的权值与A,B的父节点的权值相加求值。
在这里插入图片描述
依次类推,可以得出整棵树如下
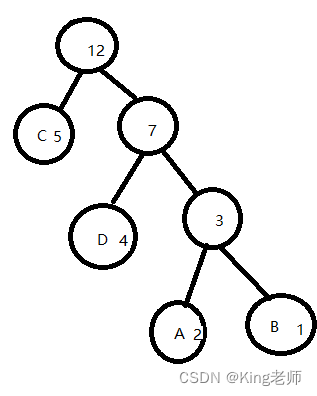
然后,把除了叶子节点的权值全部改成1.
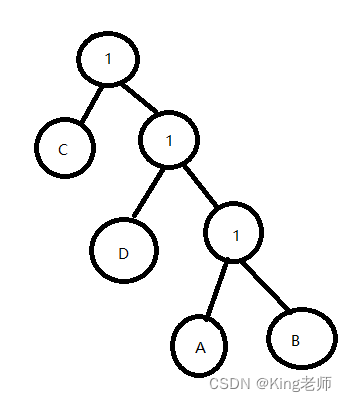
最后,叶子节点全部改成0,除B 外,B 改成1
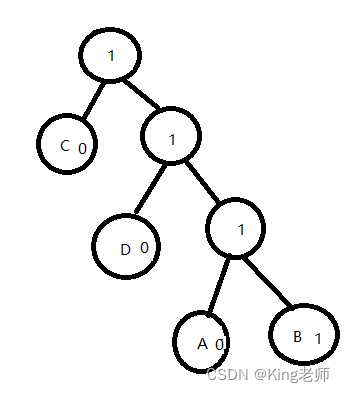
第五步,制作代号表
把左边节点权值, 我们从顶点触发,把经过的叶子节点带权路径轨迹记录下来。
第一个为: 1 - 0
第二个为: 1 - 1 - 0
第三个为: 1 - 1 - 1 - 0
第四个为: 1 - 1 -1 - 1
由此可以推出
| 代号 | 字母 |
|---|---|
| 10 | C |
| 110 | D |
| 1110 | A |
| 1111 | B |
没错,这时候你已经猜出来,为什么要这么做了。
第六步,存储
有了上面这个表格后,就可以存储和读取了。
字符串为:ACCCCCABDDD
那么按照上面的表格,分布存储为如下
1110 10 10 10 10 10 1110 1111 110 110 110
第七步,读取
我们需要根据这个树,通过轨迹来读取对于的值。

从根节点出发,遇到1走右边,遇到0走左边。
读取这串数据“1110 10 10 10 10 10 1110 1111 110 110 110”,如图
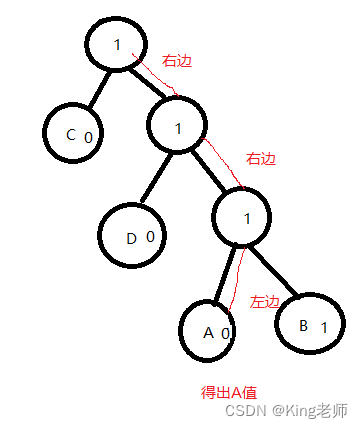
所以读取第一个值是A,(存储表的的时候是存二进制(1),这里只不过是为了好阅读)
剩下的数据为“ 10 10 10 10 10 1110 1111 110 110 110”,继续解析数据,如图
口诀: 遇到1走右边,遇到0走左边
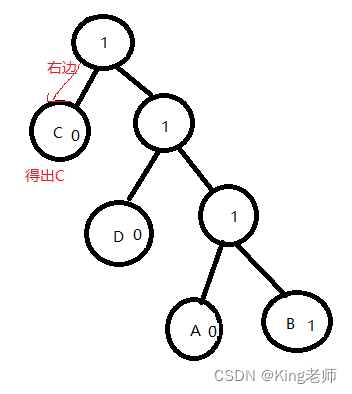
剩下的数据为“10 10 10 1110 1111 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边

剩下的数据为“ 10 10 1110 1111 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边

剩下的数据为“ 10 1110 1111 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边

剩下的数据为“ 1110 1111 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边

剩下的数据为“ 1111 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边
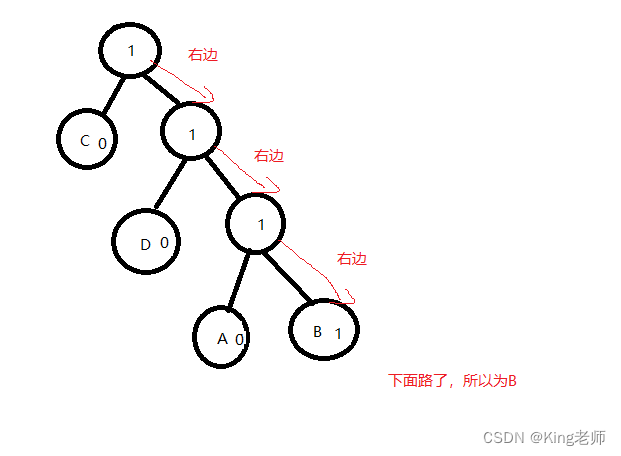
剩下的数据为“ 110 110 110”,继续解析数据,如图,
口诀: 遇到1走右边,遇到0走左边
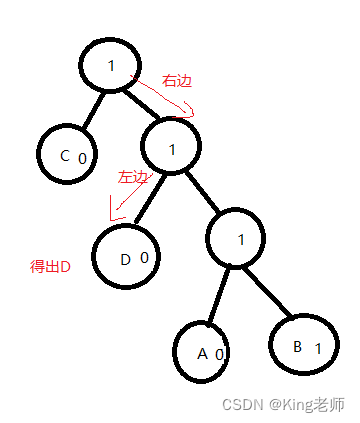
以此类推下去,全部都能解析出来。
这样的二叉树树,称为哈夫曼树。
下面是哈夫曼树的概念引用
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
由此,对比传统的存储二进制,可见节约了多少空间!通过这个规则,你已经知道为什么出现次数最多的要到前面,这样可以大大地提高读取效率。
有兴趣的朋友可以思考下图片的数据是怎么压缩的?欢迎到评论区 下留言哈哈。提示:一张图片可能有颜色值大量重复,比如一区域只有蓝色,其他全是红色的图片。
如果这篇文章有帮助到你,请点赞,评论,关注,收藏。
这篇关于7分钟0基础彻底理解常用数据压缩原理---哈夫曼编码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






