【统计分析数学模型】判别分析（二）：Fisher判别法

本文主要是介绍【统计分析数学模型】判别分析（二）：Fisher判别法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

【统计分析数学模型】判别分析（二）：Fisher判别法

一、Fisher判别法
- 1. 基本思想
- 2. 类别
- 3. R语言MASS包
二、R语言实现Fisher判别法
- 1. 使用 lda() 获得线性判别函数
- 2. 对样本进行回判分类
- 3. 混淆矩阵
- 4. 绘制散点图

一、Fisher判别法

1. 基本思想

Fisher判别法的基本思想是“投影”，即将高维空间中的样本点投影到低维空间，从而简化问题。

Fisher判别最重要的就是选出适当的投影轴，保证投影后每一类之内的样本点的离散程度尽可能小，而不同类之间的样本点的离散程度尽可能大。

2. 类别

Fisher判别有线性判别、二次判别等多种判别方法。

对于线性判别，先将样本点投影到一维空间（即直线）上，若效果不好，则可以增加一个维度，即投影到二维空间中，以此类推。

二次判别与线性判别的区别在于投影面的形状不同，线性判别的投影面为直线或平面，而二次判别使用若干二次曲面将样本点划分到相应的类别中。

3. R语言MASS包

MASS包里的函数lda()可用于线性判别，函数qda()可用于二次判别。

线性判别函数
lda(x, ...)
二次判别函数
qda(x, ...)

二、R语言实现Fisher判别法

1. 使用 lda() 获得线性判别函数

在公式里Diagnosis为因变量，其余5个变量为自变量；先验概率的默认值为各个类别所占的比例

library(MASS)
thyroid.ld<-lda(Diagnosis~RT3U+T4+T3+TSH+DTSH,data=thyroid)
thyroid.ld

输出中包括函数lda()里所用的公式、先验概率、各类的均值向量、线性判别函数的系数、两个判别式对区分总体的贡献大小等：

> thyroid.ld
Call:
lda(Diagnosis ~ RT3U + T4 + T3 + TSH + DTSH, data = thyroid)Prior probabilities of groups:Normal     Hyper      Hypo 
0.6976744 0.1627907 0.1395349 Group means:RT3U        T4       T3        TSH      DTSH
Normal 110.51333  9.192667 1.731333  1.3166667  2.516667
Hyper   95.28571 17.745714 4.262857  0.9742857 -0.020000
Hypo   121.70000  3.600000 1.063333 12.9200000 17.533333Coefficients of linear discriminants:LD1          LD2
RT3U  0.02501083  0.001974564
T4   -0.30544670 -0.103495742
T3   -0.11588398 -0.434103730
TSH   0.03831828 -0.147419858
DTSH  0.07288461 -0.074044771Proportion of trace:LD1    LD2 
0.8398 0.1602 
>

两个线性判别函数分别为：

LD1 = 0.025×RT3U - 0.305×T4 - 0.116×T3 + 0.038×TSH + 0.073×DTSH

LD2 = 0.002×RT3U - 0.103×T4 - 0.434×T3 - 0.147×TSH - 0.074×DTSH

2. 对样本进行回判分类

将泛型函数predict()作用于线性判别对象可以得到各个样品的回判分类：

thyroid.pred<-predict(thyroid.ld)
thyroid.pred$class

结果如下：

> thyroid.pred$class[1] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[11] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[21] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[31] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[41] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[51] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[61] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[71] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[81] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal[91] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[101] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[111] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[121] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[131] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[141] Normal Normal Normal Normal Normal Normal Normal Normal Normal Normal
[151] Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Normal
[161] Hyper  Hyper  Normal Hyper  Hyper  Normal Hyper  Hyper  Normal Hyper 
[171] Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Hyper  Normal Hyper  Normal
[181] Hyper  Normal Normal Hyper  Normal Hypo   Hypo   Normal Normal Hypo  
[191] Hypo   Hypo   Hypo   Hypo   Hypo   Hypo   Normal Hypo   Hypo   Hypo  
[201] Hypo   Hypo   Hypo   Hypo   Hypo   Hypo   Hypo   Hypo   Hypo   Hypo  
[211] Normal Normal Normal Normal Normal
Levels: Normal Hyper Hypo

3. 混淆矩阵

与上一篇文章（距离判别法）类似，我们可以通过混淆矩阵查看判别效果：

table(thyroid.pred$class,thyroid$Diagnosis)

结果如下：

> table(thyroid.pred$class,thyroid$Diagnosis)Normal Hyper HypoNormal    150     9    8Hyper       0    26    0Hypo        0     0   22

结果表明，有17个样品判别错误，错误率为7.9%，正确率为92.1%。

被错判的对象所处的行号：

e1<-which(thyroid.pred$class=="Normal"&thyroid$Diagnosis=="Hyper")
e2<-which(thyroid.pred$class=="Normal"&thyroid$Diagnosis=="Hypo")

> e1
[1] 160 163 166 169 178 180 182 183 185> e2
[1] 188 189 197 211 212 213 214 215

4. 绘制散点图

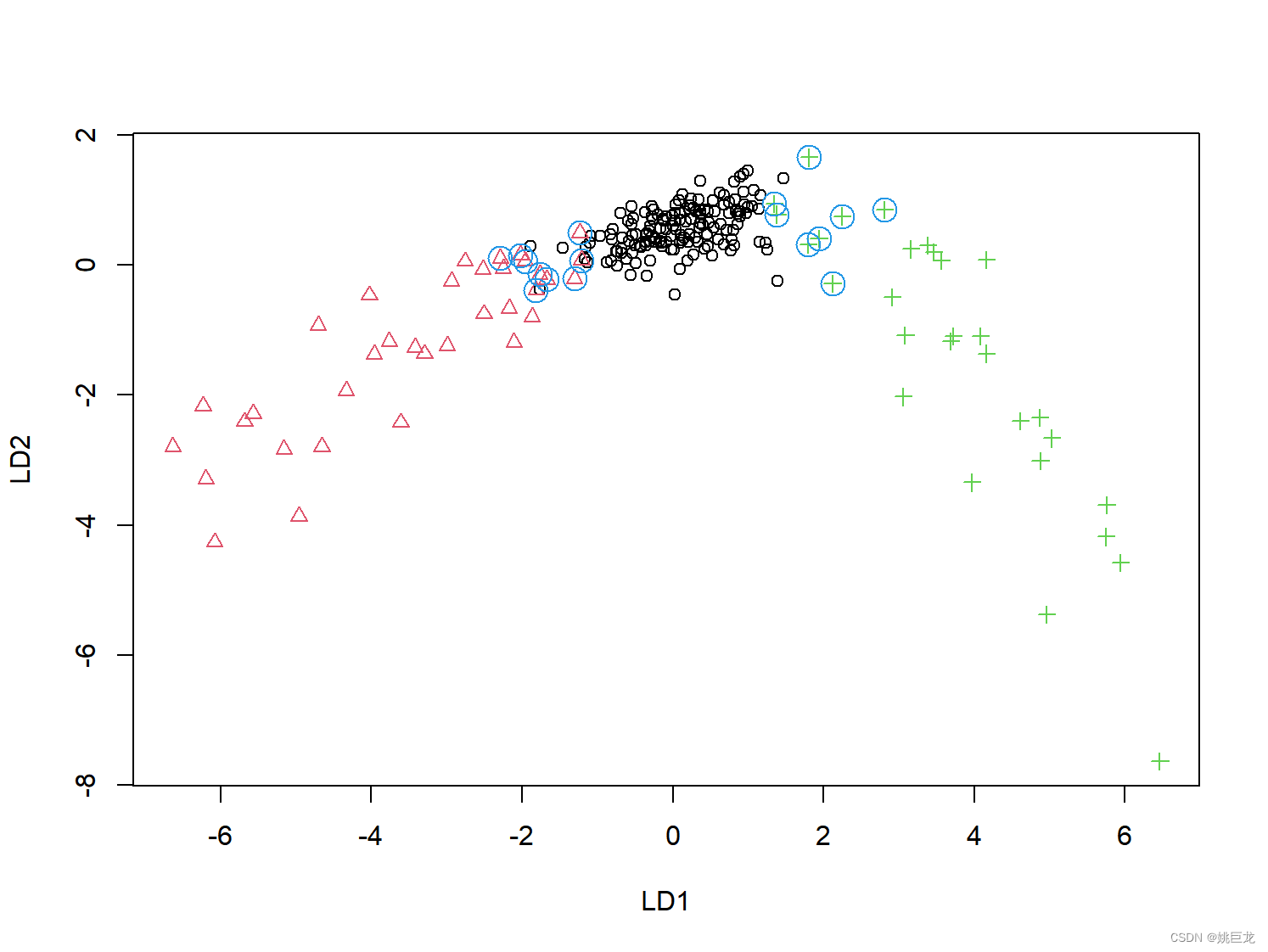
以两个线性判别函数为坐标轴绘制散点图，并用不同颜色和形状的点表示患者的诊断类型：

LD1<-thyroid.pred$x[,1]
LD2<-thyroid.pred$x[,2]
col<-as.numeric(thyroid$Diagnosis)
pch<-as.numeric(thyroid$Diagnosis)
plot(LD1,LD2,col=col,pch=pch)
legend("bottom",legend=c("Normal","Hyper","Hypo"),+col=1:3,pch=1:3)
points(LD1[e1],LD2[e1],cex=2,col=4)
points(LD1[e2],LD2[e2],cex=2,col=4)