本文主要是介绍(done) 矩阵的对角化,以及是否可对角化的判断、还有对角化的本质。相似对角化计算过程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
相似对角化 和 对角化 很大程度上是一回事
甚至判断两个矩阵的相似性,也跟对角化有很大关系
参考视频1:https://www.bilibili.com/video/BV1PA411T7b5/?spm_id_from=333.788&vd_source=7a1a0bc74158c6993c7355c5490fc600
参考视频2:https://www.bilibili.com/video/BV14T4y127jf/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
参考视频3:https://www.bilibili.com/video/BV1Js4y1372V/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
如下图的矩阵其实可以看成一个 “基向量” 变换,它把 (1, 0) 变成 (2, 1),把 (0, 1) 变成 (1, 2)

同时,我们把自然基下的矢量,使用上述矩阵进行变换时,大部分矢量的方向会被改变,但有部分矢量的方向是不会被改变的,如下图,这类矢量我们就称为特征向量

平面内还有另一个特征向量 (它总是保持不变吗?还是说只是因为特征值刚好是 1?与原特征向量垂直是必须的吗?)
这两个特征向量,似乎在自然基和变换基下,都是垂直的?
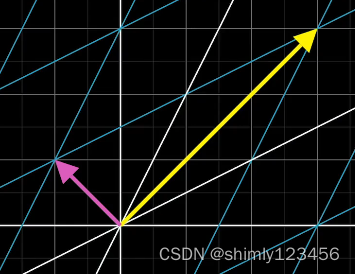
此时,可以把这两个特征向量作为一组新的基,那么,原来的变换矩阵在这个新的基下的作用就只是把矢量进行伸缩。于是,原来的变换矩阵在这个新的基下的作用就可以使用一个 “对角阵” 来表示
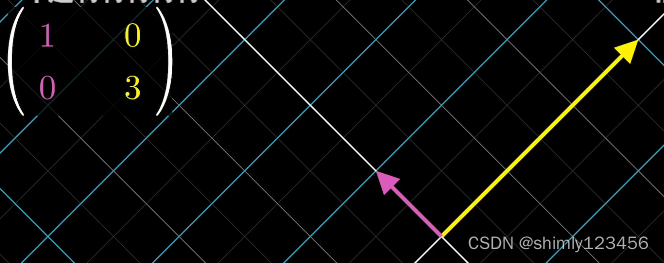
因此,这个 对角阵 和 原来的变换矩阵 是相似的。
X 和 X^(-1) 就是基变换矩阵,它们由 自然基 下的特征向量构成
一个更好的理解是,原来的变换矩阵可以拆分成:
1.先把自然基下的矢量映射到 “特征向量构成的一组基” 上
2.在 “特征向量构成的一组基” 上对矢量进行变换 (实际上就是伸缩)
3.再把变换后的矢量映射回 自然基 上

当我们把 基变换矩阵 的顺序改变时,对角矩阵的顺序也需要变换
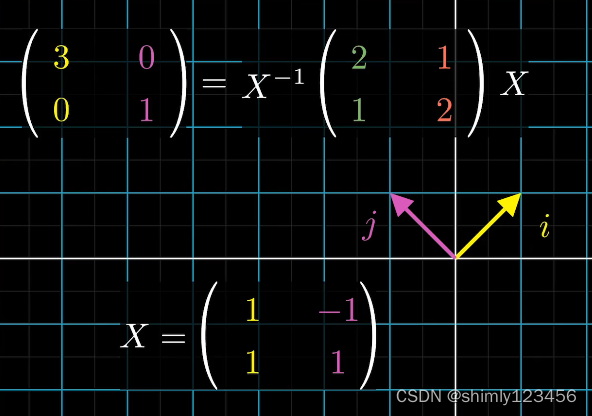
此时就可以明白,一个矩阵能否相似对角化的充要条件是 “它的特征向量能否构成一组基”

构成一组基的条件:即这组特征向量是线性无关的
更精确的说法:矩阵A 有 n 个线性无关的特征向量

以下是一个小的引理
若有 n 个不同的特征值 =====> 则 A 有 n 个线性无关的特征向量 (不同特征值对应的特征向量线性无关)
NOTE: 反过来不一定成立哦!

如下图,是一个例子:
若三阶矩阵有三个特征值,那么它就可对角化,因为它拥有三个线性无关的特征向量
若只有 1, 2, 2,那就要重点关注 (lamda = 2) 所对应的特征向量,若它们线性无关,则可对角化;否则不行

以下是一个求特征值、特征向量,从而把矩阵相似对角化的例子:

当 lamda1 = lamda2 = 2 时,我们发现求出的矩阵只有一个非零行,那么也就是说它的 “自由未知量” 是 2。
这其实暗含了 “我们能够得到两个线性无关非零解” 的意思,也就说这个矩阵是可以相似对角化的

这篇关于(done) 矩阵的对角化,以及是否可对角化的判断、还有对角化的本质。相似对角化计算过程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







